- 快召唤伙伴们来围观吧
- 微博 QQ QQ空间 贴吧
- 文档嵌入链接
- 复制
- 微信扫一扫分享
- 已成功复制到剪贴板
Using Apache Pulsar to Provide Real-Time IoT Analytics on the Edge
展开查看详情
1 .REAL-TIME IOT ANALYTICS WITH APACHE PULSAR DAVID KJERRUMGAARD JUNE 18TH, 2020
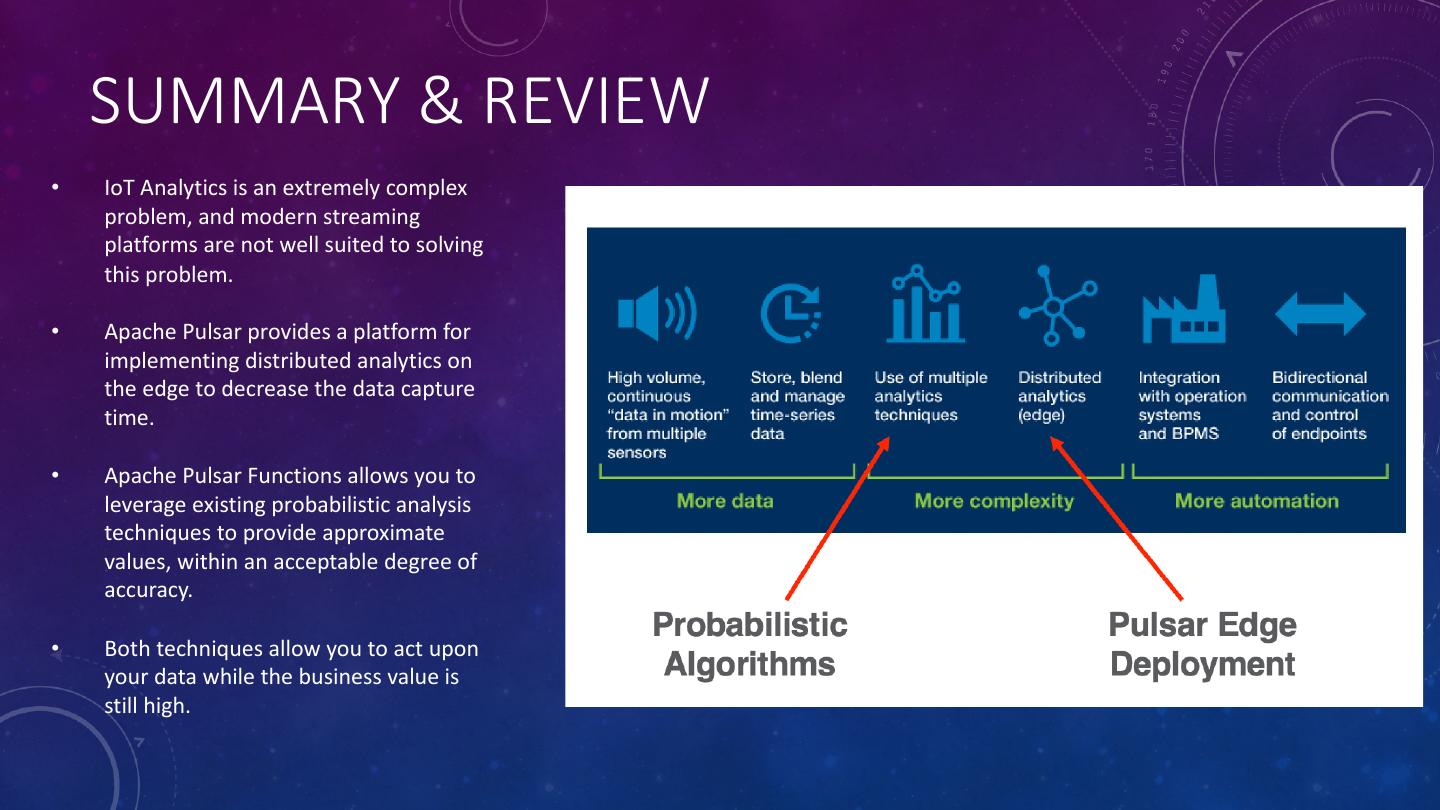
2 .DEFINING IOT ANALYTICS • It is NOT JUST loading sensor data into a data lake to create predictive analytic models. While this is crucial piece of the puzzle, it is not the only one. • IoT Analytics requires the ability to ingest, aggregate, and process an endless stream of real-time data coming off a wide variety of sensor devices “at the edge” • IoT Analytics renders real-time decisions at the edge of the network to either optimize operational performance or detect anomalies for immediate remediation.
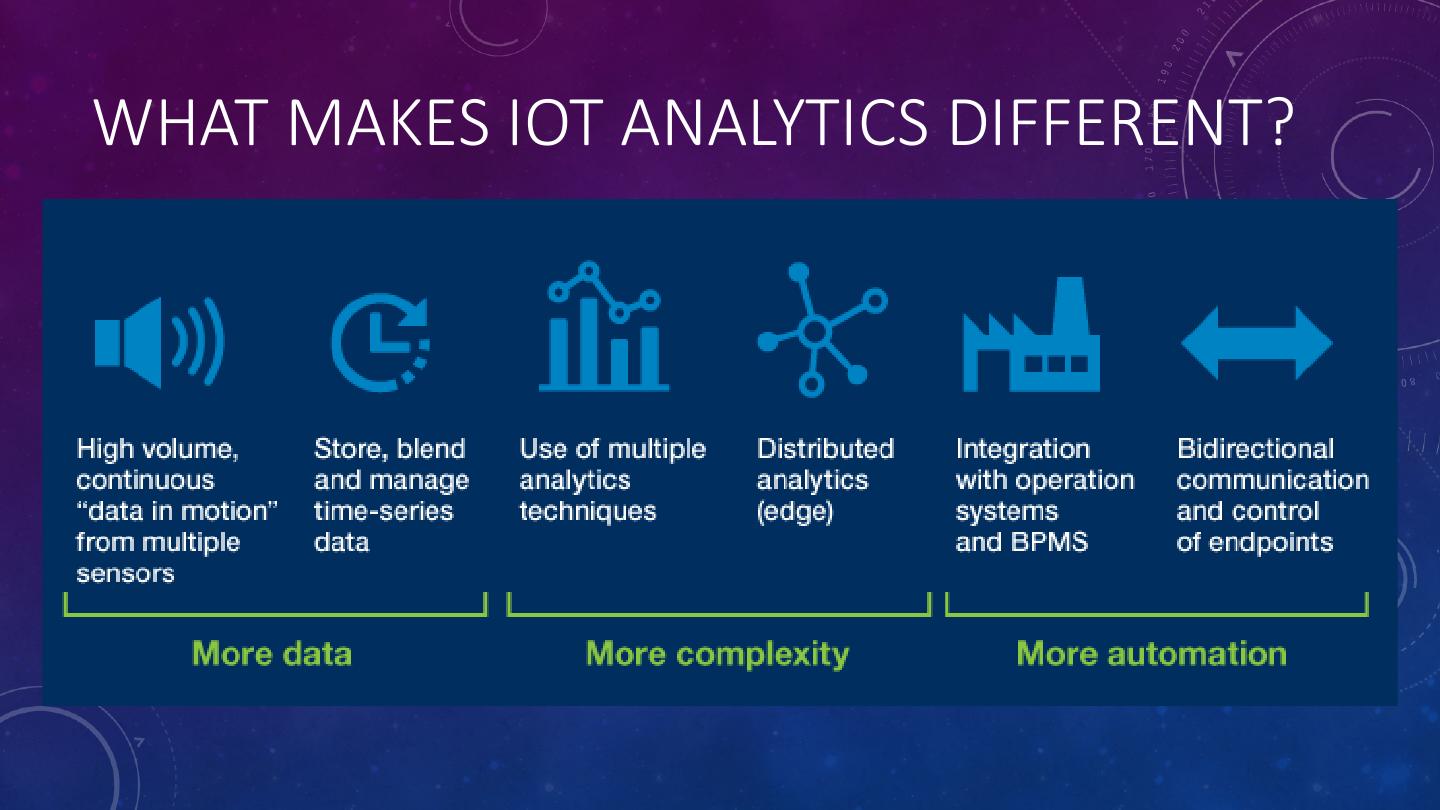
3 .WHAT MAKES IOT ANALYTICS DIFFERENT?
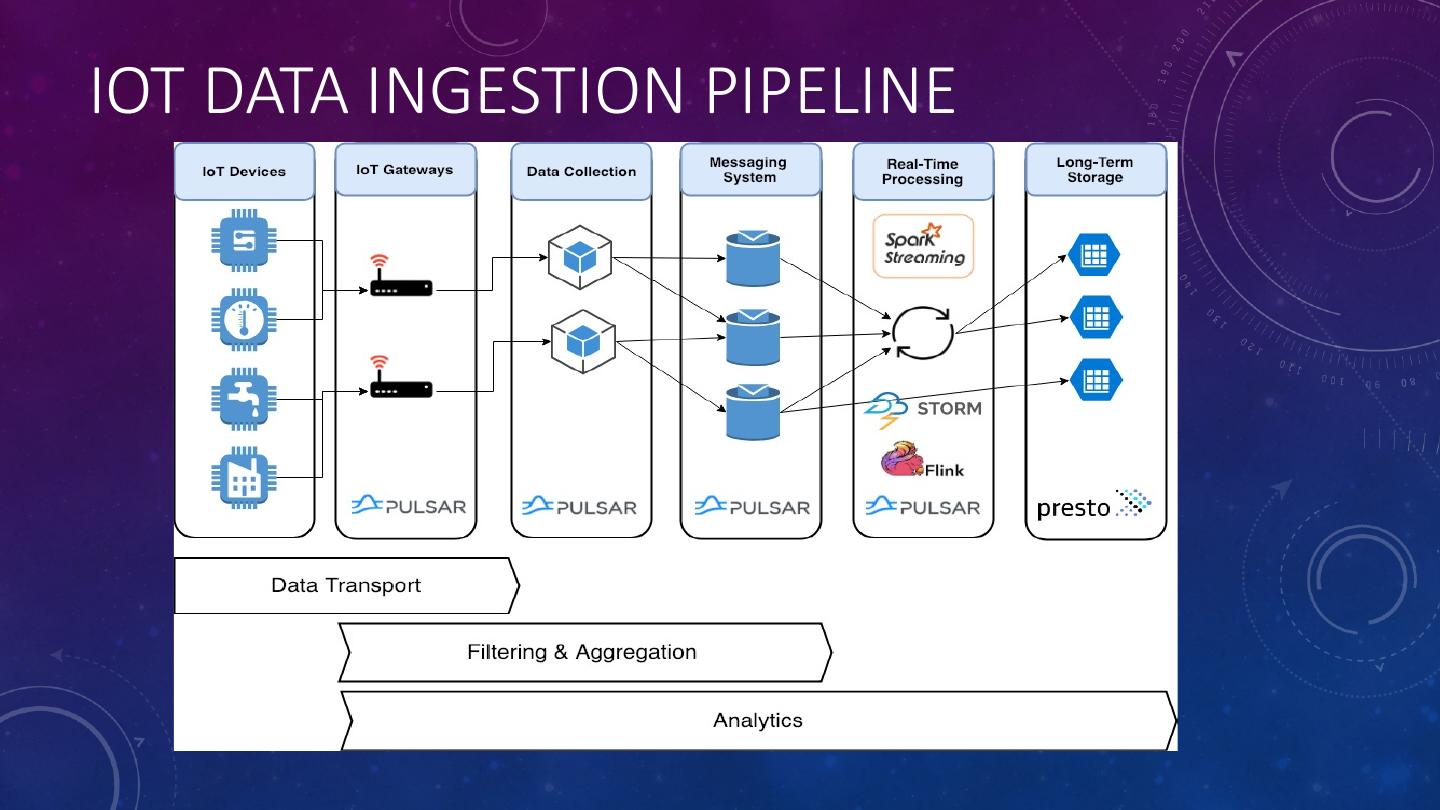
4 .IOT ANALYTICS CHALLENGES • IoT deals with machine generated data consisting of discrete observations such as temperature, vibration, pressure, etc. that is produced at very high rates. • We need an architecture that: • Allows us to quickly identify and react to anomalous events • Reduces the volume of data transmitted back to the data lake. • In this talk, we will present a solution based on Apache Pulsar Functions that distributes the analytics processing across all tiers of the IoT data ingestion pipeline.
5 .IOT DATA INGESTION PIPELINE
6 .APACHE PULSAR FUNCTIONS
7 .PULSAR FUNCTIONS: STREAM PROCESSING The Apache Pulsar platform provides a flexible, serverless computing framework that allows you execute user-defined functions to process and transform data. • Implemented as simple methods but allows you to leverage existing libraries and code within Java or Python code. • Functions execute against every single event that is published to a specified topic and write their results to another topic. Forming a logical directed- acyclic graph. • Enable dynamic filtering, transformation, routing and analytics. • Can run anywhere a JVM can, including edge devices.
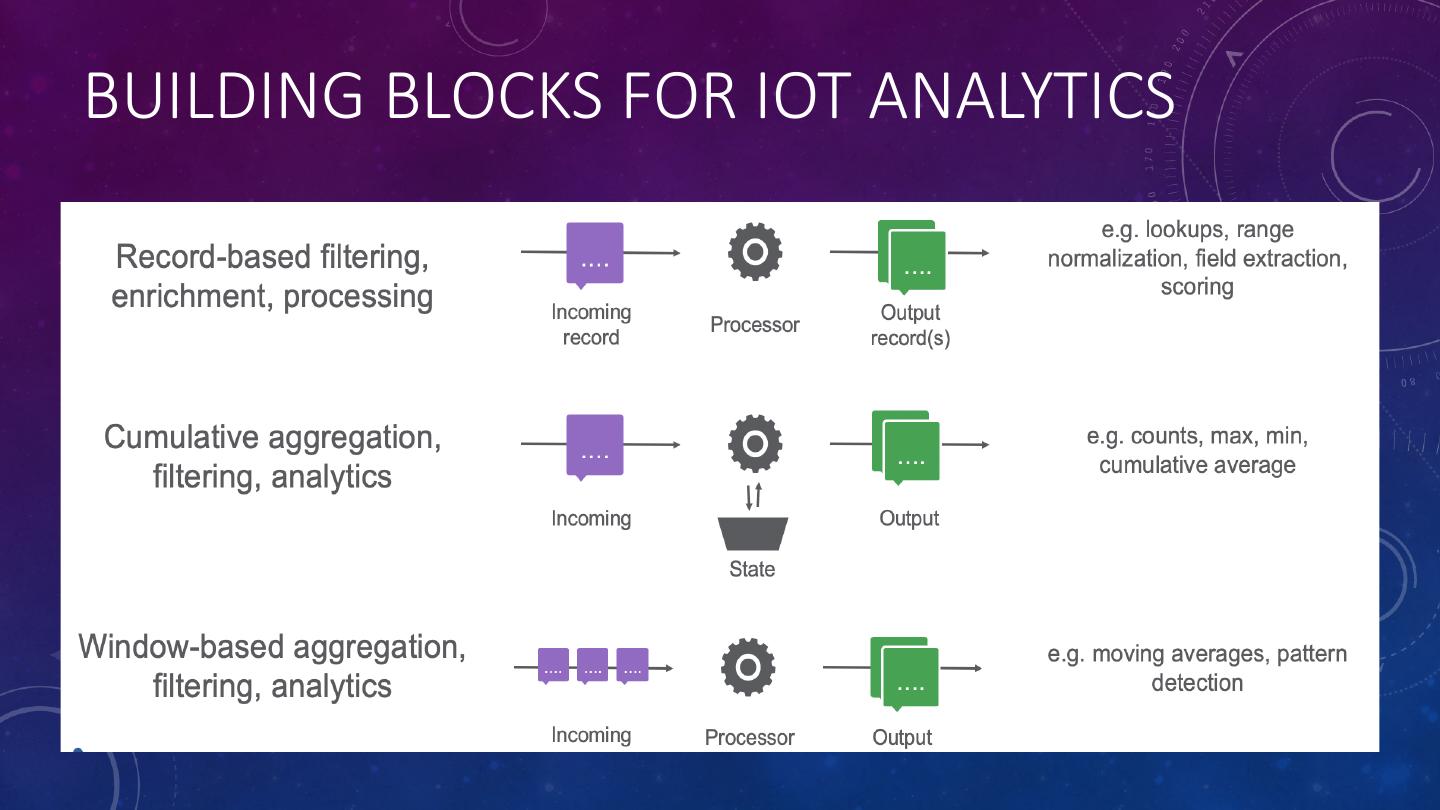
8 .BUILDING BLOCKS FOR IOT ANALYTICS
9 .DISTRIBUTED PROBABILISTIC ANALYTICS WITH APACHE PULSAR FUNCTIONS
10 .PROBABILISTIC ANALYSIS • Often times, it is sufficient to provide an approximate value when it is impossible and/or impractical to provide a precise value. In many cases having an approximate answer within a given time frame is better than waiting for an exact answer. • Probabilistic algorithms can provide approximate values when the event stream is either too large to store in memory, or the data is moving too fast to process. • Instead of requiring to keep such enormous data on-hand, we leverage algorithms that require only a few kilobytes of data.
11 .DATA SKETCHES • A central theme throughout most of these probabilistic data structures is the concept of data sketches, which are designed to require only enough of the data necessary to make an accurate estimation of the correct answer. • Typically, sketches are implemented a bit arrays or maps thereby requiring memory on the order of Kilobytes, making them ideal for resource-constrained environments, e.g. on the edge. • Sketching algorithms only need to see each incoming item only once, and are therefore ideal for processing infinite streams of data.
12 .SKETCH EXAMPLE • Let’s walk through an demonstration to show exactly what I mean by sketches and show you that we do not need 100% of the data in order to make an accurate prediction of what the picture contains • How much of the data did you require to identify the main item in the picture?
13 .DATA SKETCH PROPERTIES • Configurable Accuracy • Sketches sized correctly can be 100% accurate • Error rate is inversely proportional to size of a Sketch • Fixed Memory Utilization • Maximum Sketch size is configured in advance • Memory cost of a query is thus known in advance • Allows Non-additive Operations to be Additive • Sketches can be merged into a single Sketch without over counting • Allows tasks to be parallelized and combined later • Allows results to be combined across windows of execution
14 .OPERATIONS SUPPORTED BY SKETCHES
15 .SOME SKETCHY FUNCTIONS
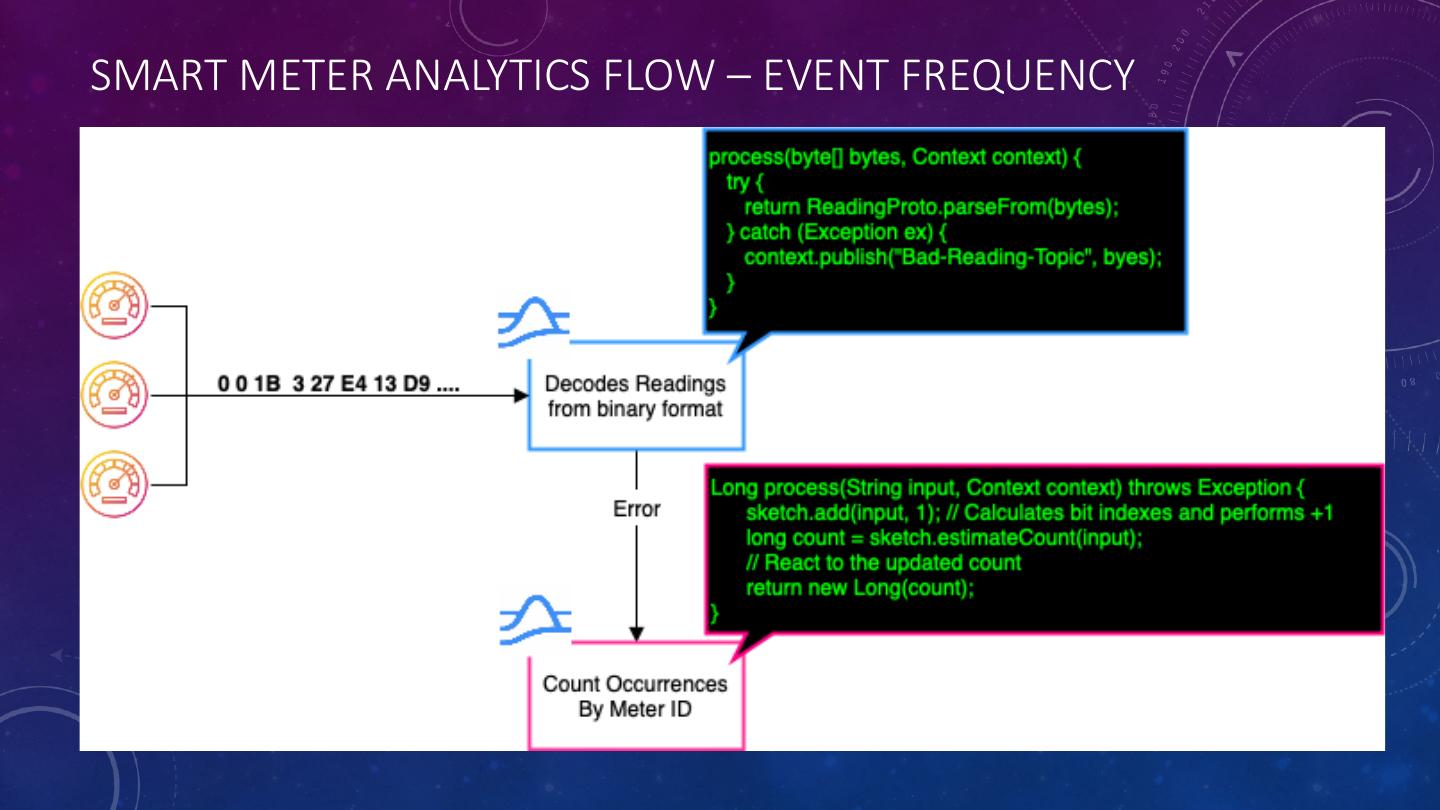
16 .EVENT FREQUENCY • Another common statistic computed is the frequency at which a specific element occurs within an endless data stream with repeated elements, which enables us to answer questions such as; “How many times has element X occurred in the data stream?”. • Consider trying to analyze and sample the IoT sensor data for just a single industrial plant that can produce millions of readings per second. There isn’t enough time to perform the calculations or store the data. • In such a scenario you can chose to forego an exact answer, which will we never be able to compute in time, for an approximate answer that is within an acceptable range of accuracy.
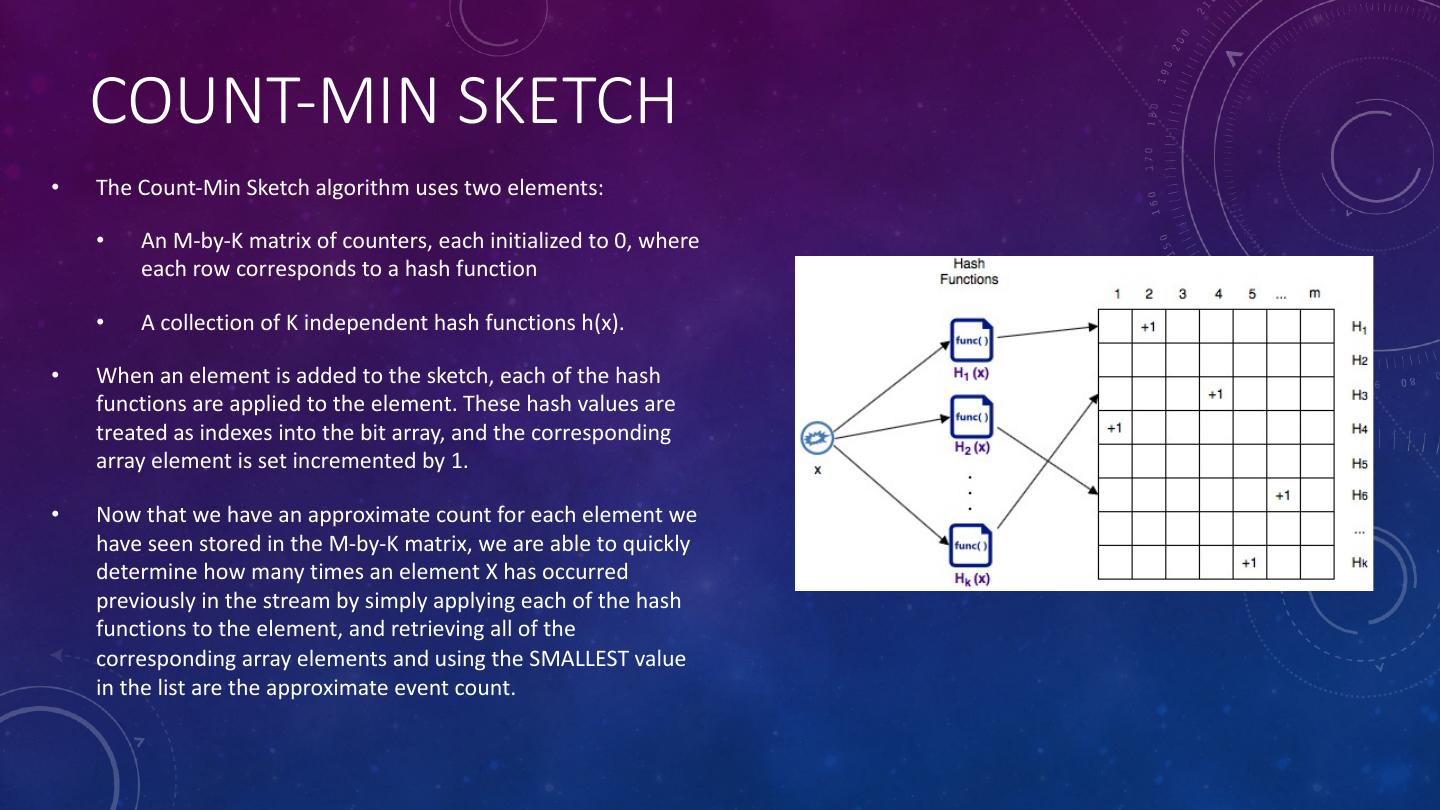
17 . COUNT-MIN SKETCH • The Count-Min Sketch algorithm uses two elements: • An M-by-K matrix of counters, each initialized to 0, where each row corresponds to a hash function • A collection of K independent hash functions h(x). • When an element is added to the sketch, each of the hash functions are applied to the element. These hash values are treated as indexes into the bit array, and the corresponding array element is set incremented by 1. • Now that we have an approximate count for each element we have seen stored in the M-by-K matrix, we are able to quickly determine how many times an element X has occurred previously in the stream by simply applying each of the hash functions to the element, and retrieving all of the corresponding array elements and using the SMALLEST value in the list are the approximate event count.
18 .PULSAR FUNCTION: EVENT FREQUENCY import org.apache.pulsar.functions.api.Context; import org.apache.pulsar.functions.api.Function; import com.clearspring.analytics.stream.frequency.CountMinSketch; public class CountMinFunction implements Function<String, Long> { CountMinSketch sketch = new CountMinSketch(20,20,128); Long process(String input, Context context) throws Exception { sketch.add(input, 1); // Calculates bit indexes and performs +1 long count = sketch.estimateCount(input); // React to the updated count return new Long(count); } }
19 .K-FREQUENCY-ESTIMATION • Another common use of the Count-Min algorithm is maintaining lists of frequent items which is commonly referred to as the “Heavy Hitters”. This design pattern retains a list of items that occur more frequently than some predefined value, e.g. the top-K list • The K-Frequency-Estimation problem can also be solved by using the Count-Min Sketch algorithm. The logic for updating the counts is exactly the same as in the Event Frequency use case. • However, there is an additional list of length K used to keep the top-K elements seen that is updated.
20 . PULSAR FUNCTION: TOP K import org.apache.pulsar.functions.api.Context; import org.apache.pulsar.functions.api.Function; import com.clearspring.analytics.stream.StreamSummary; public class CountMinFunction implements Function<String, List<Counter<String>>> { StreamSummary<String> summary = new StreamSummary<String> (256); List<Counter<String>> process(String input, Context context) throws Exception { // Add the element to the sketch summary.offer(input, 1) // Grab the updated top 10 List<Counter<String>> topK = summary.topK(10); return topK; } }
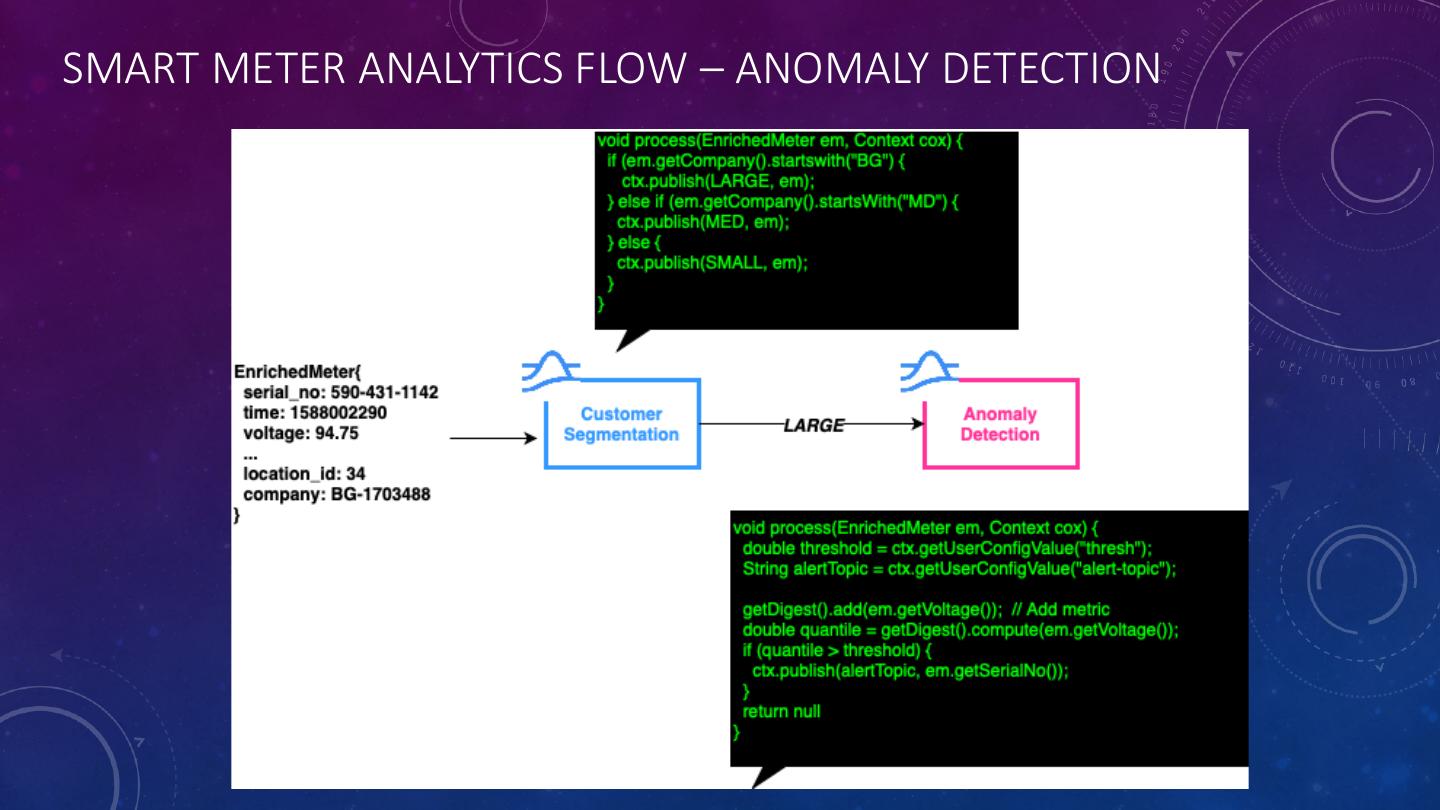
21 . ANOMALY DETECTION • The most anomaly detectors use a manually configured threshold value that is not adaptive to even simple patterns or variances. • Instead of using a single static value for our thresholds, we should consider using quantiles instead. • In statistics and probably, quantiles are used to represent probability distributions. The most common of which are known as percentiles.
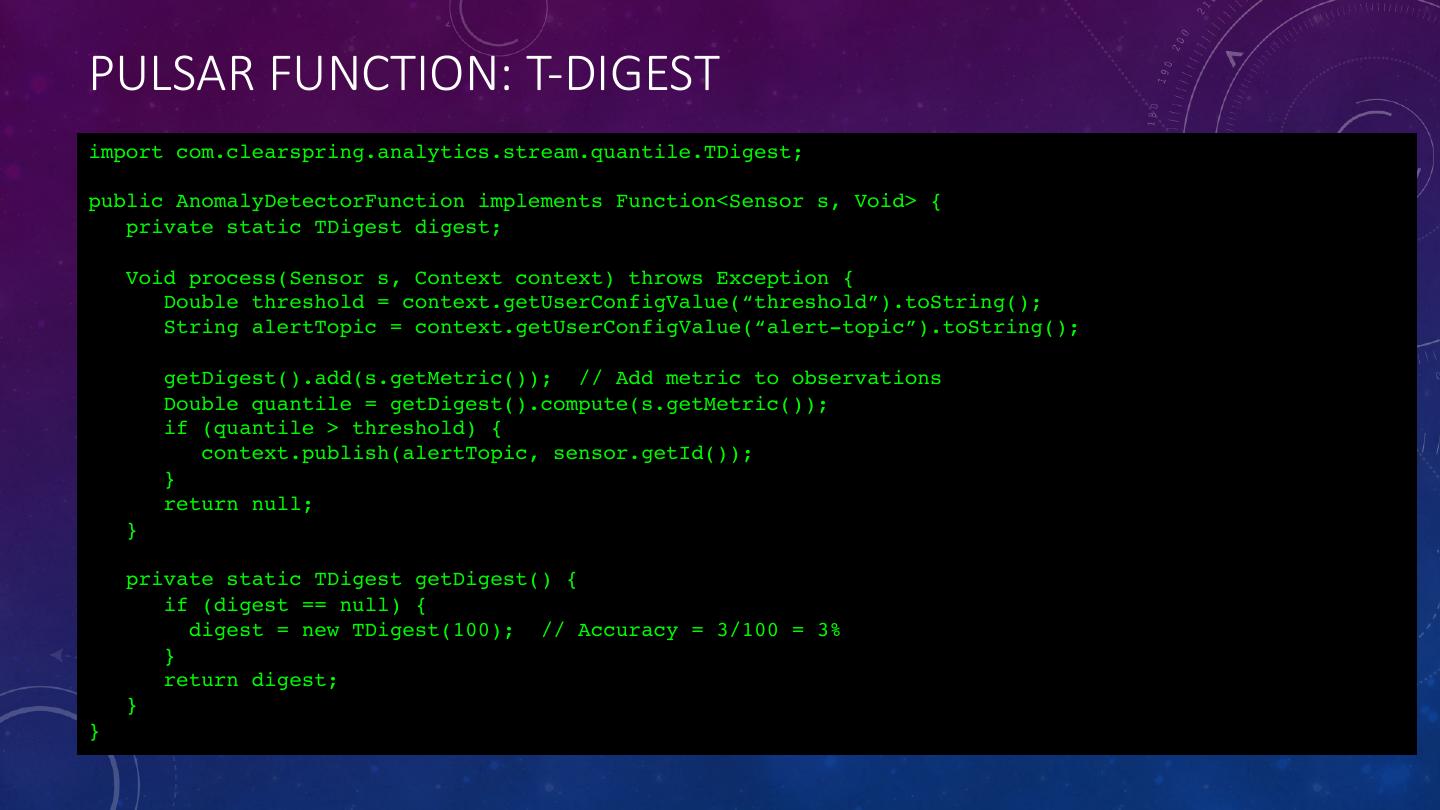
22 .ANOMALY DETECTION WITH QUANTILES • The data structure known as t-digest was developed by Ted Dunning, as a way to accurately estimate extreme quantiles for very large data sets with limited memory use. • This capability makes t-digest particularly useful for calculating quantiles that can be used to select a good threshold for anomaly detection. • The advantage of this approach is that the threshold automatically adapts to the dataset as it collects more data.
23 .PULSAR FUNCTION: T-DIGEST import com.clearspring.analytics.stream.quantile.TDigest; public AnomalyDetectorFunction implements Function<Sensor s, Void> { private static TDigest digest; Void process(Sensor s, Context context) throws Exception { Double threshold = context.getUserConfigValue(“threshold”).toString(); String alertTopic = context.getUserConfigValue(“alert-topic”).toString(); getDigest().add(s.getMetric()); // Add metric to observations Double quantile = getDigest().compute(s.getMetric()); if (quantile > threshold) { context.publish(alertTopic, sensor.getId()); } return null; } private static TDigest getDigest() { if (digest == null) { digest = new TDigest(100); // Accuracy = 3/100 = 3% } return digest; } }
24 .IOT ANALYTICS PIPELINE USING APACHE PULSAR FUNCTIONS
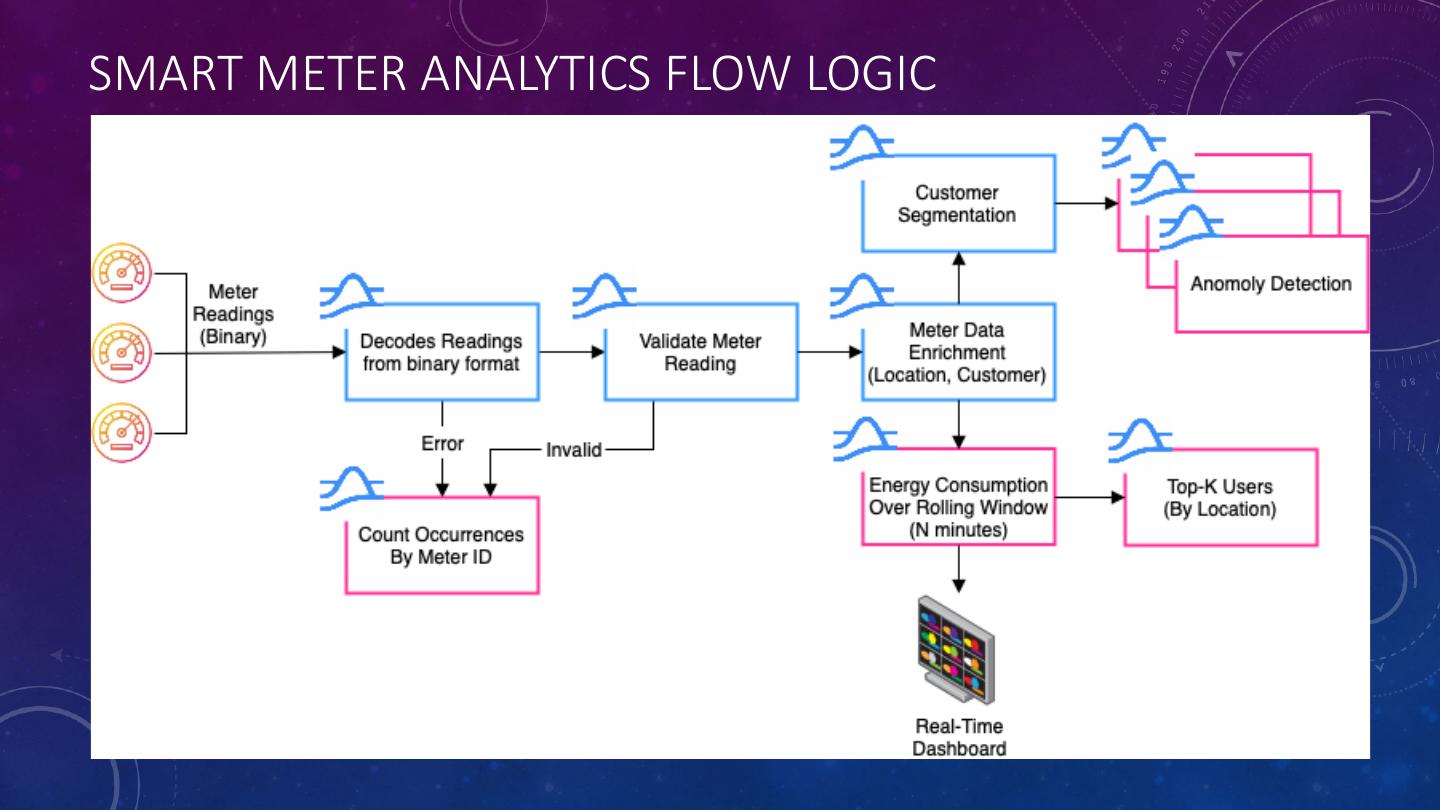
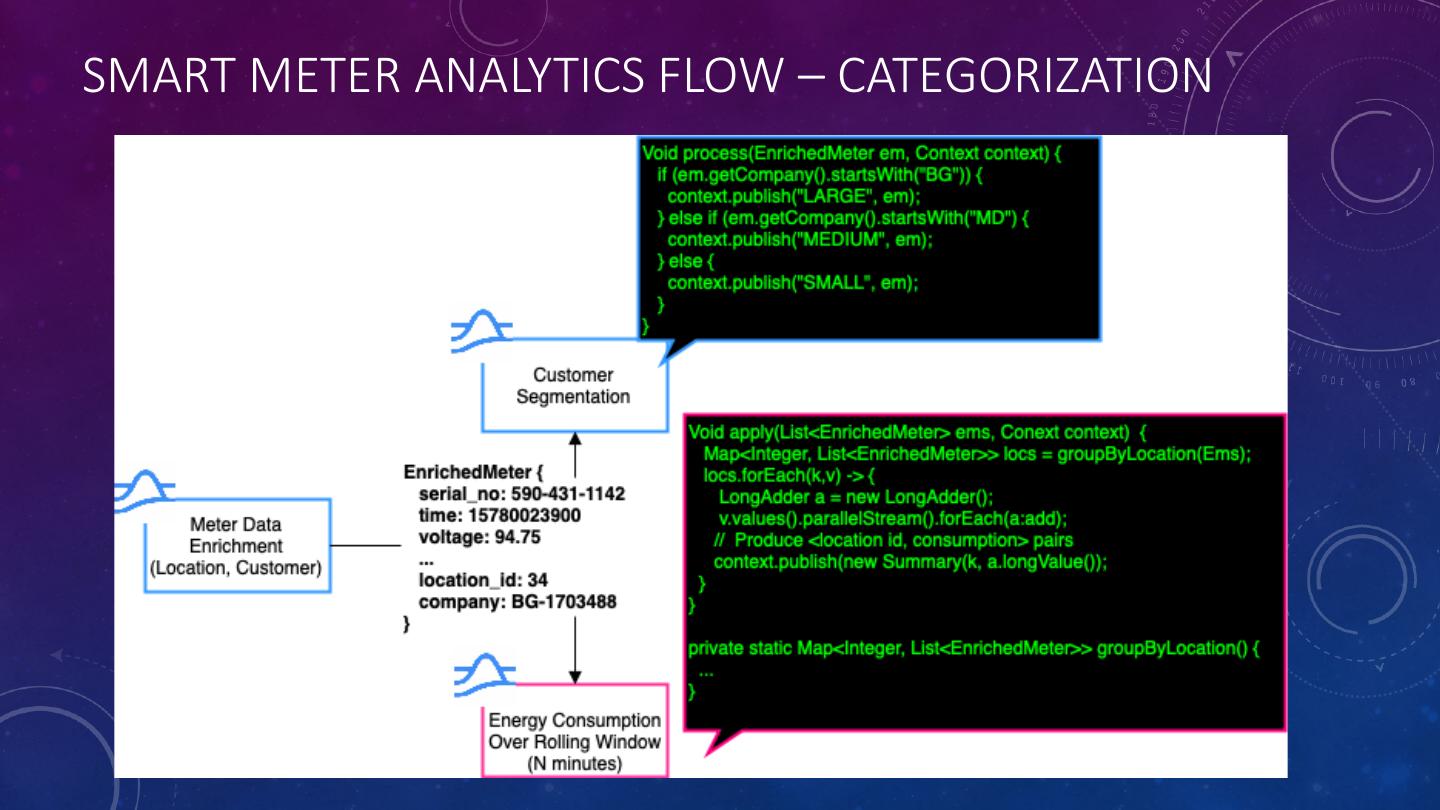
25 .IDENTIFYING REAL-TIME ENERGY CONSUMPTION PATTERNS • A network of smart meters enables utilities companies to gain greater visibility into their customers energy consumption. • Increase/decrease energy generation to meet the demand • Implement dynamic notifications to encourage consumers to use less energy during peak demand periods. • Provide real-time revenue forecasts to senior business leaders. • Identify fault meters and schedule maintenance calls to repair them.
26 .SMART METER ANALYTICS FLOW LOGIC
27 .SMART METER ANALYTICS FLOW – EVENT FREQUENCY
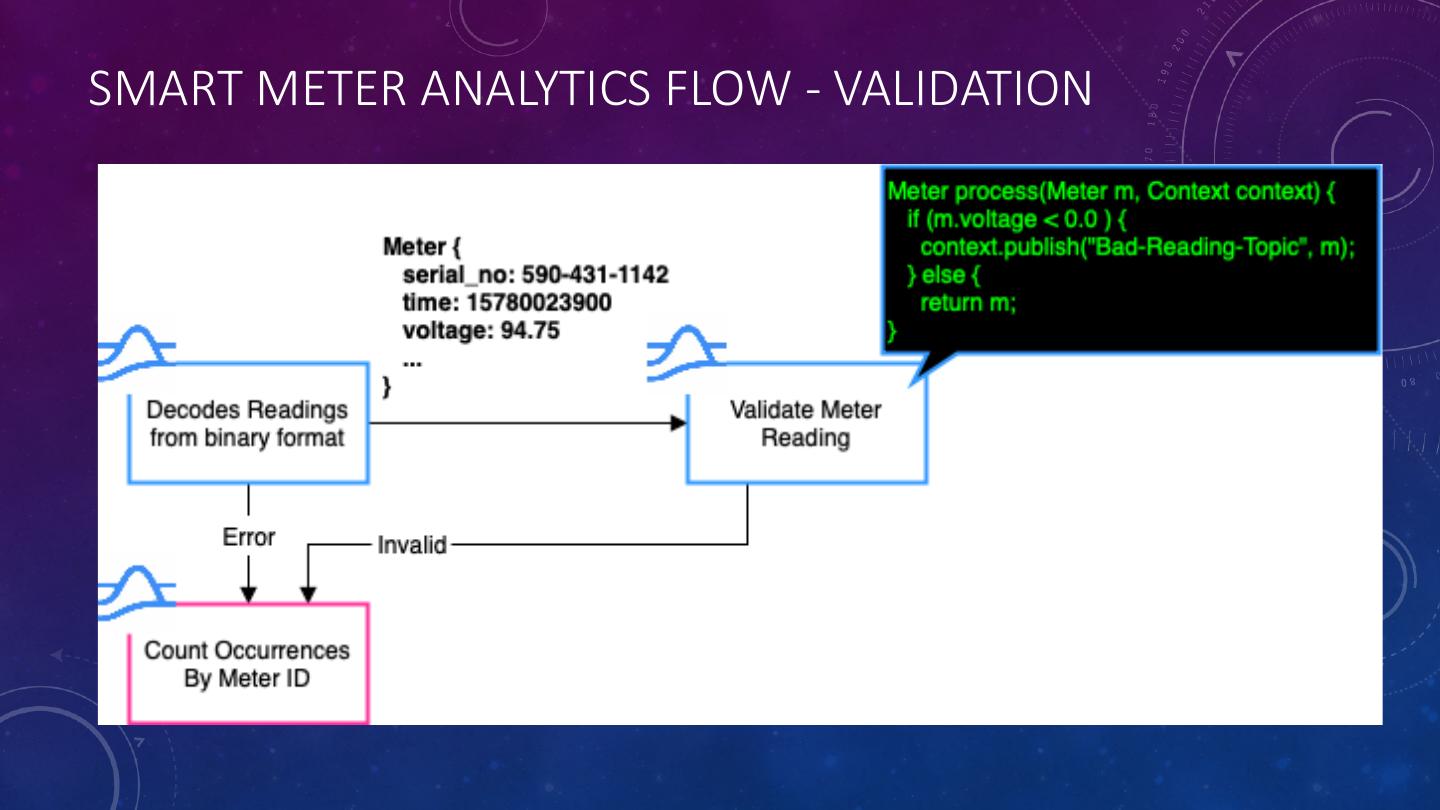
28 .SMART METER ANALYTICS FLOW - VALIDATION
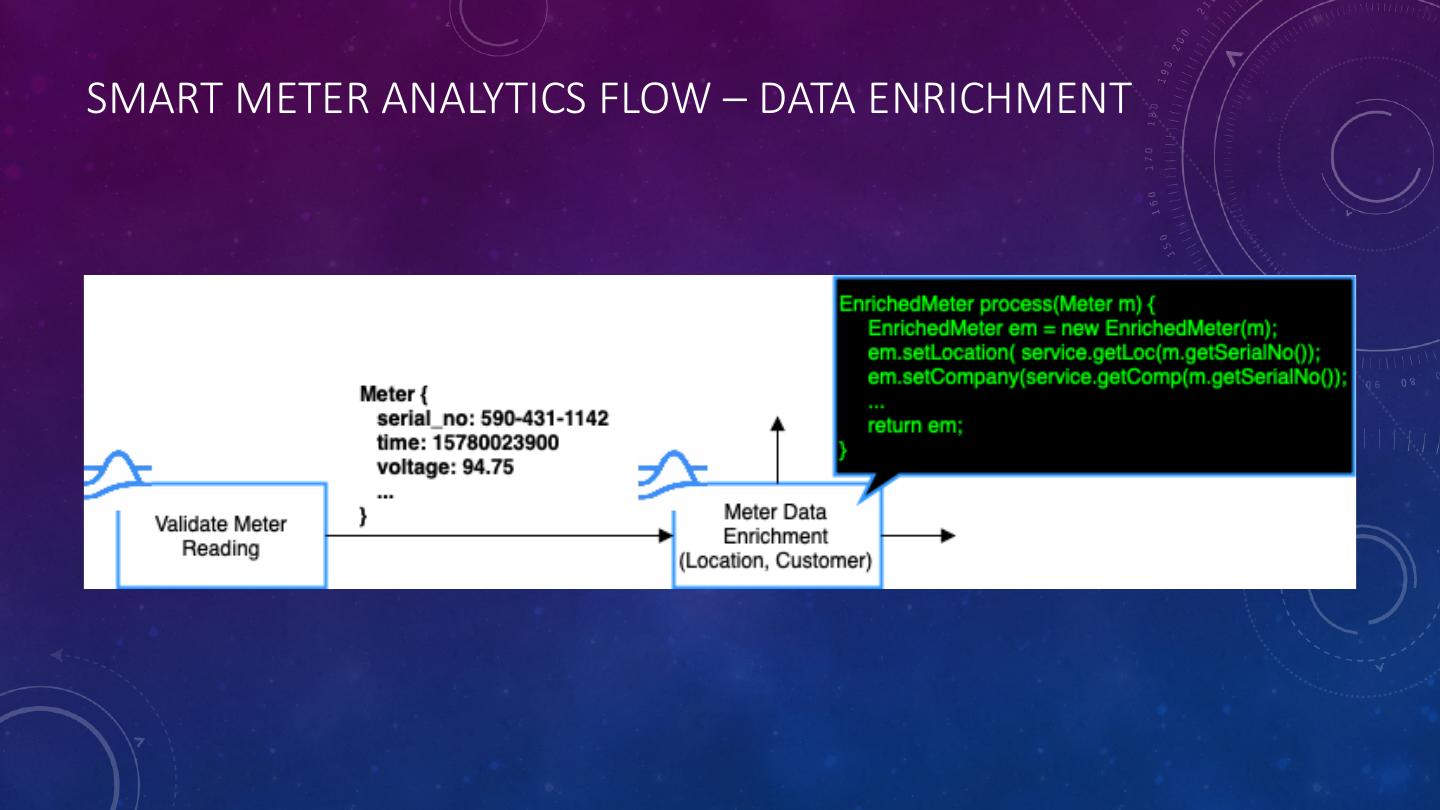
29 .SMART METER ANALYTICS FLOW – DATA ENRICHMENT