08_Regression

1 .Computer vision: models, learning and inference Chapter 8 Regression

2 .Structure 2 2 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince Linear regression Bayesian solution Non-linear regression Kernelization and Gaussian processes Sparse linear regression Dual linear regression Relevance vector regression Applications

3 .Models for machine vision 3 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince

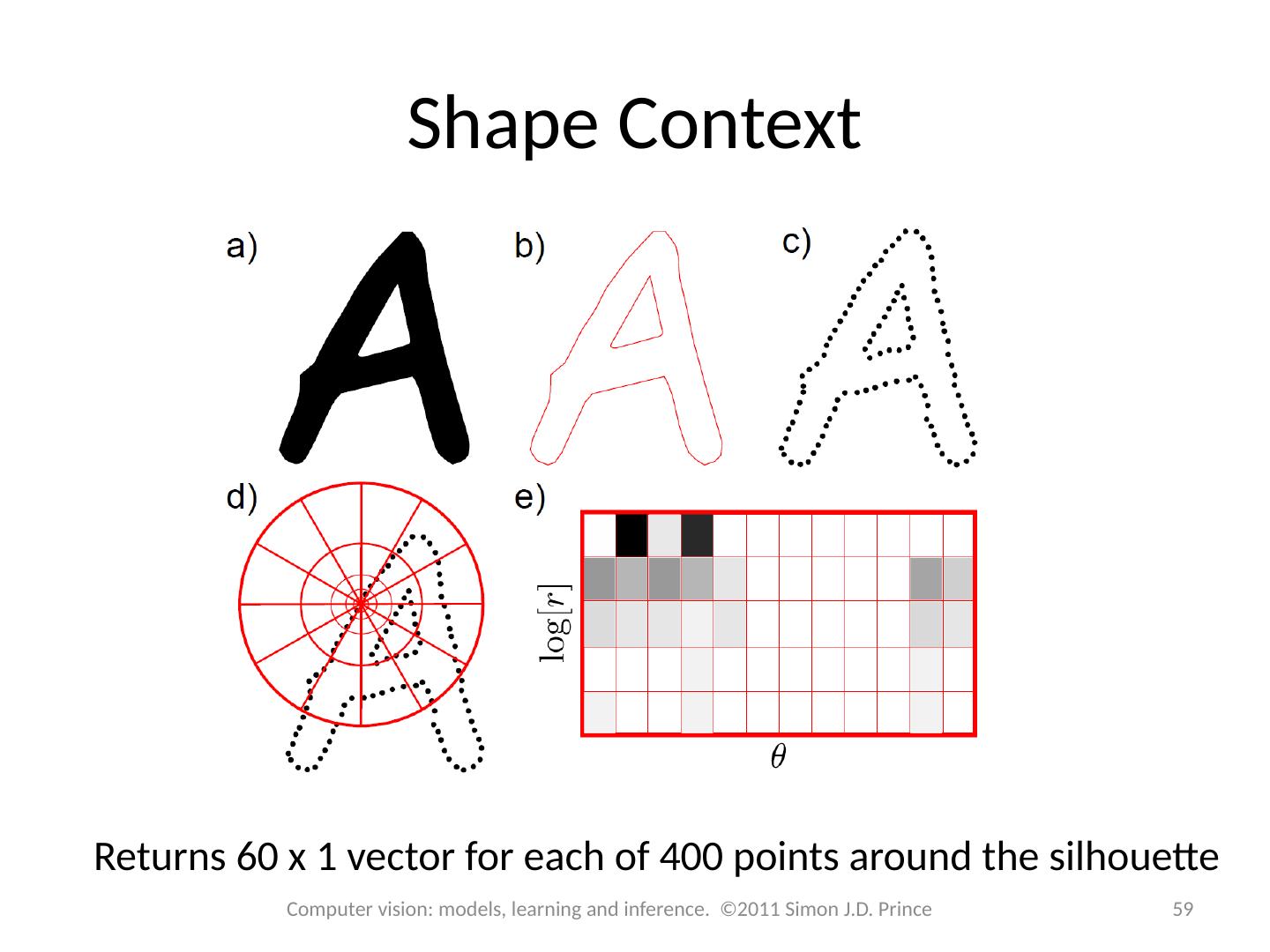
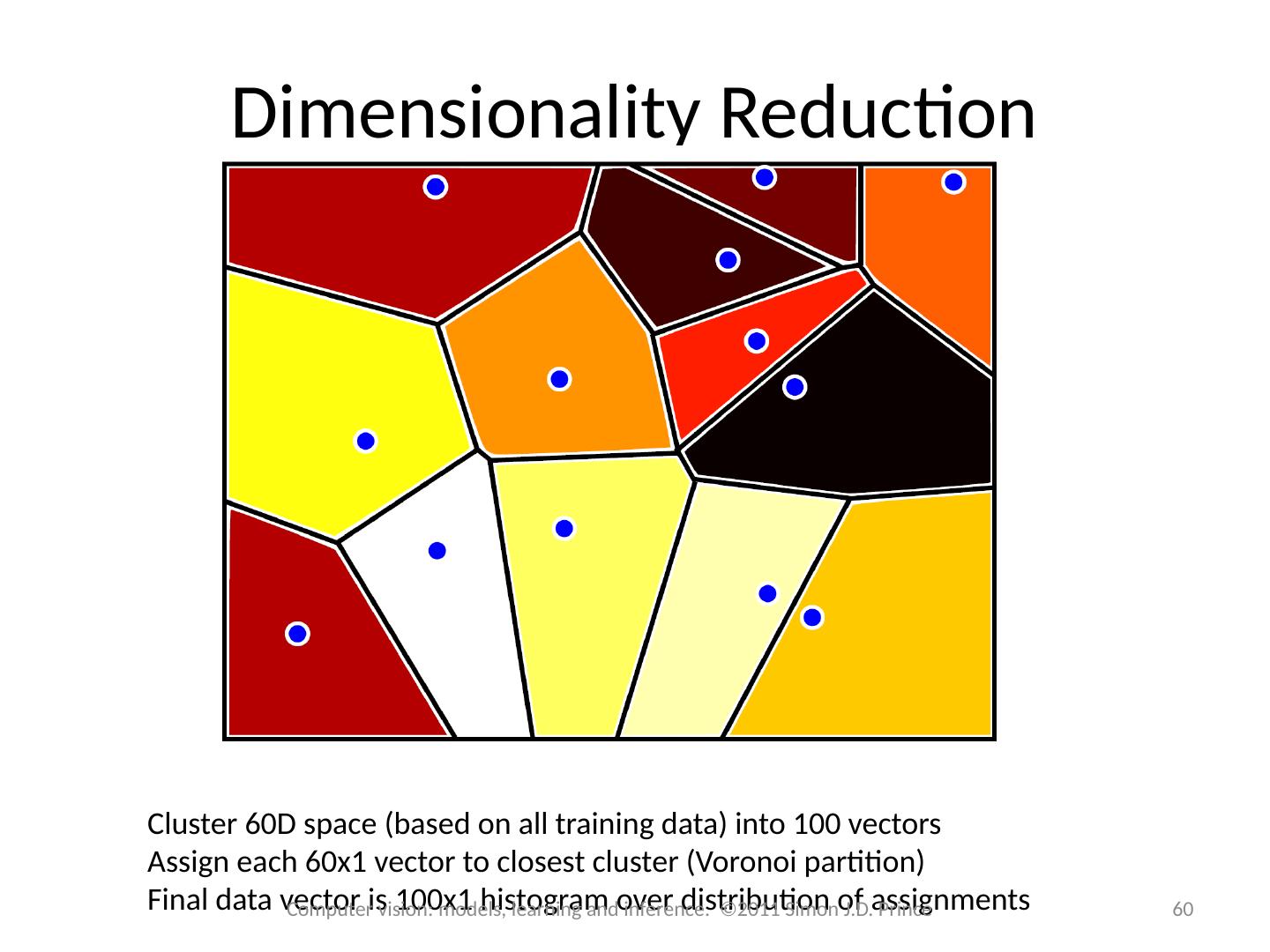
4 .Body Pose Regression Encode silhouette as 100x1 vector, encode body pose as 55 x1 vector. Learn relationship 4 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince

5 .Type 1: Model Pr( w | x ) - Discriminative How to model Pr( w | x )? Choose an appropriate form for Pr( w ) Make parameters a function of x Function takes parameters q that define its shape Learning algorithm : learn parameters q from training data x , w Inference algorithm : just evaluate Pr( w|x ) 5 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince

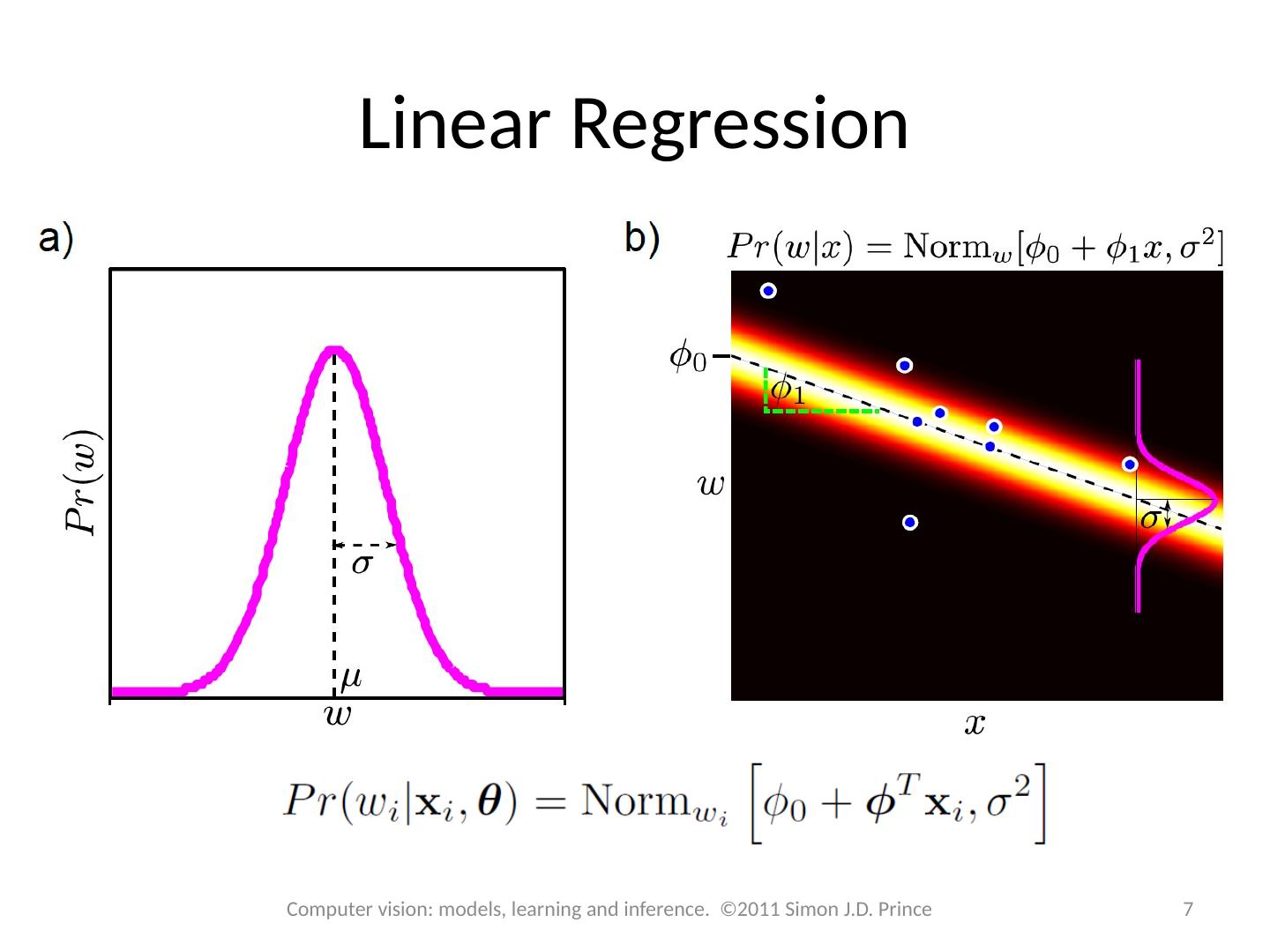
6 .Linear Regression For simplicity we will assume that each dimension of world is predicted separately. Concentrate on predicting a univariate world state w. Choose normal distribution over world w Make Mean a linear function of data x Variance constant 6 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince

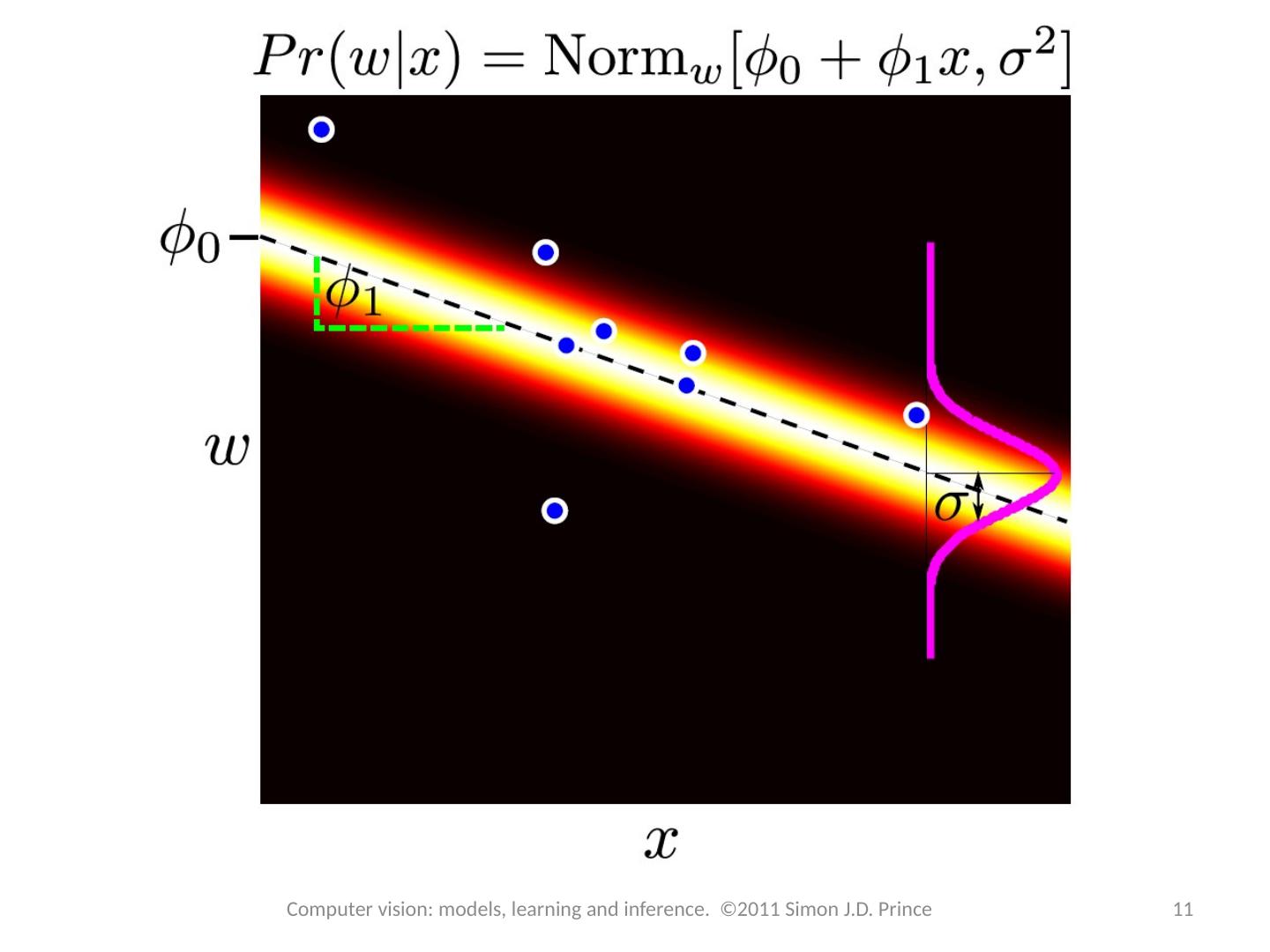
7 .Linear Regression 7 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince

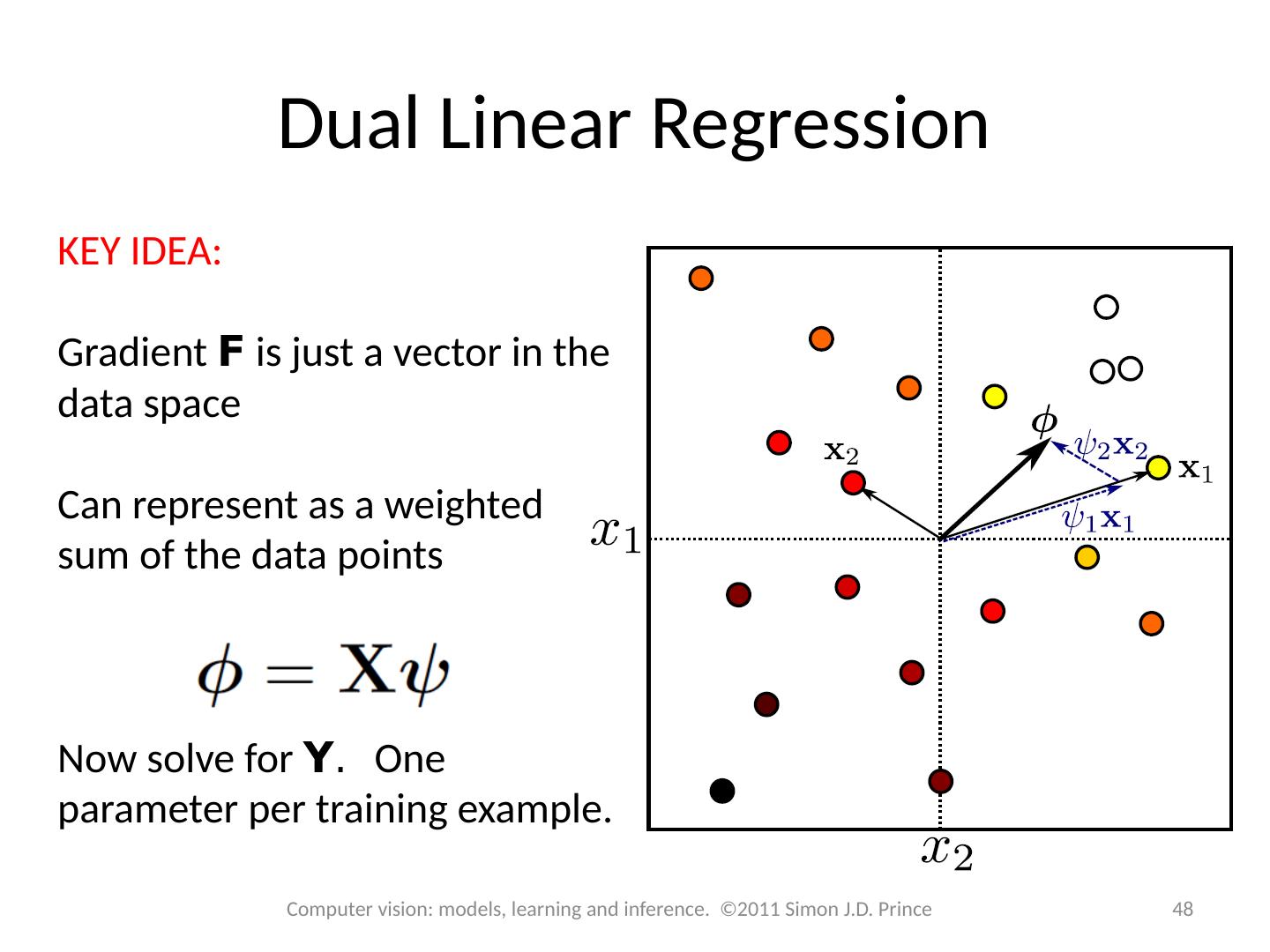
8 .Neater Notation To make notation easier to handle, we Attach a 1 to the start of every data vector Attach the offset to the start of the gradient vector f New model: 8 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince

9 .Combining Equations We have one equation for each x,w pair: The likelihood of the whole dataset is the product of these individual distributions and can be written as where 9 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince

10 .Learning Maximum likelihood Substituting in Take derivative, set result to zero and re-arrange: 10 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince

11 .11 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince

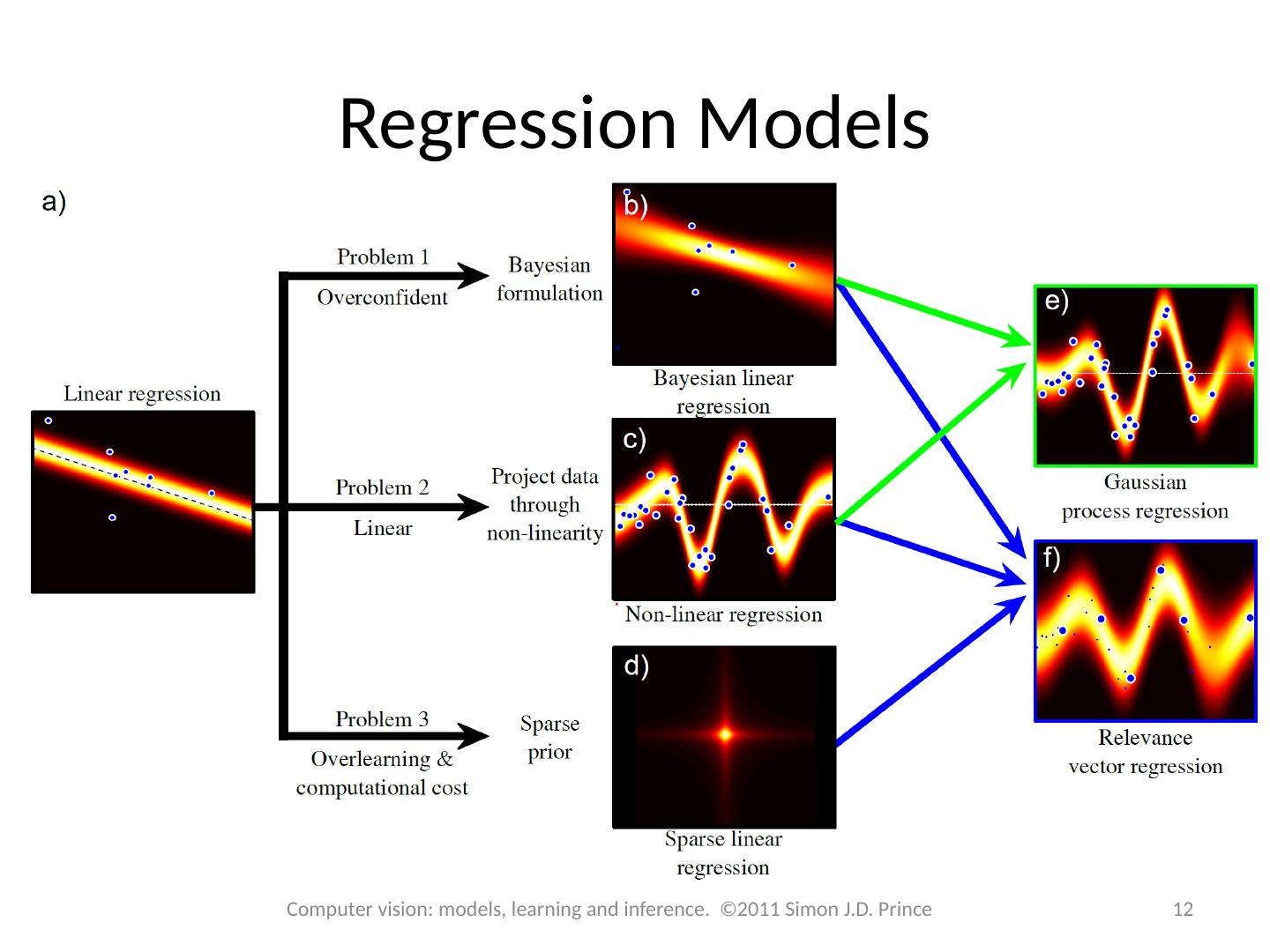
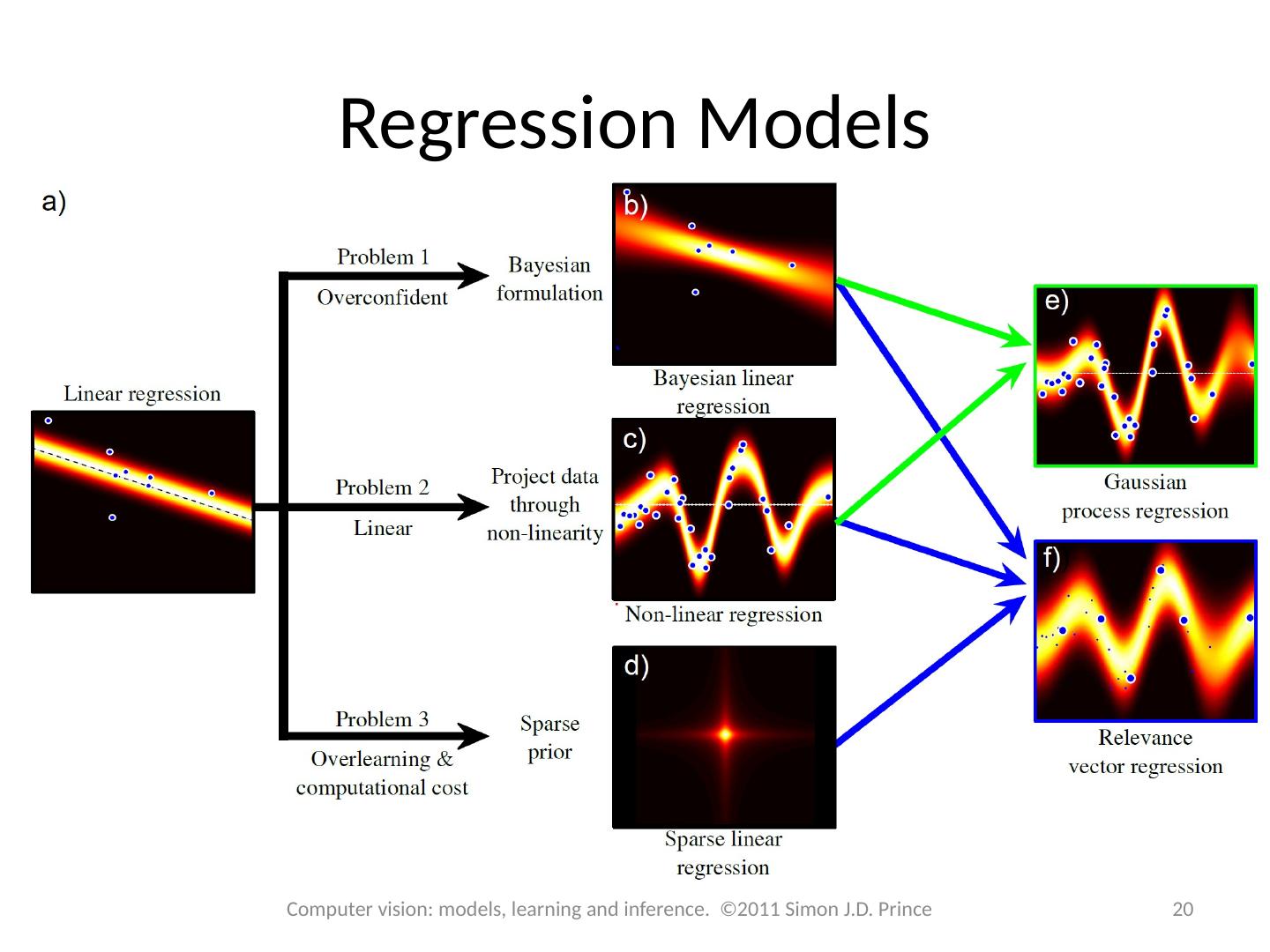
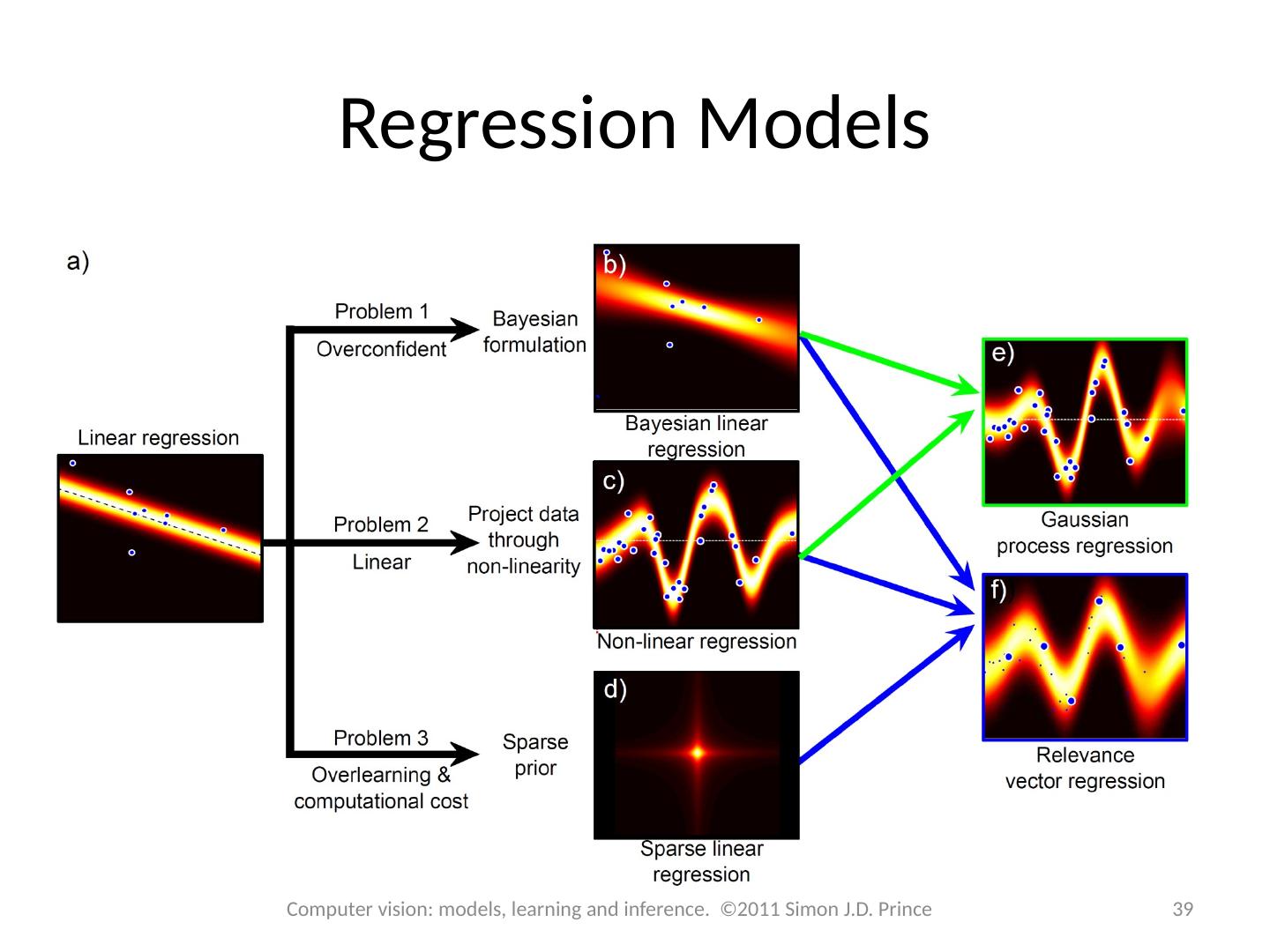
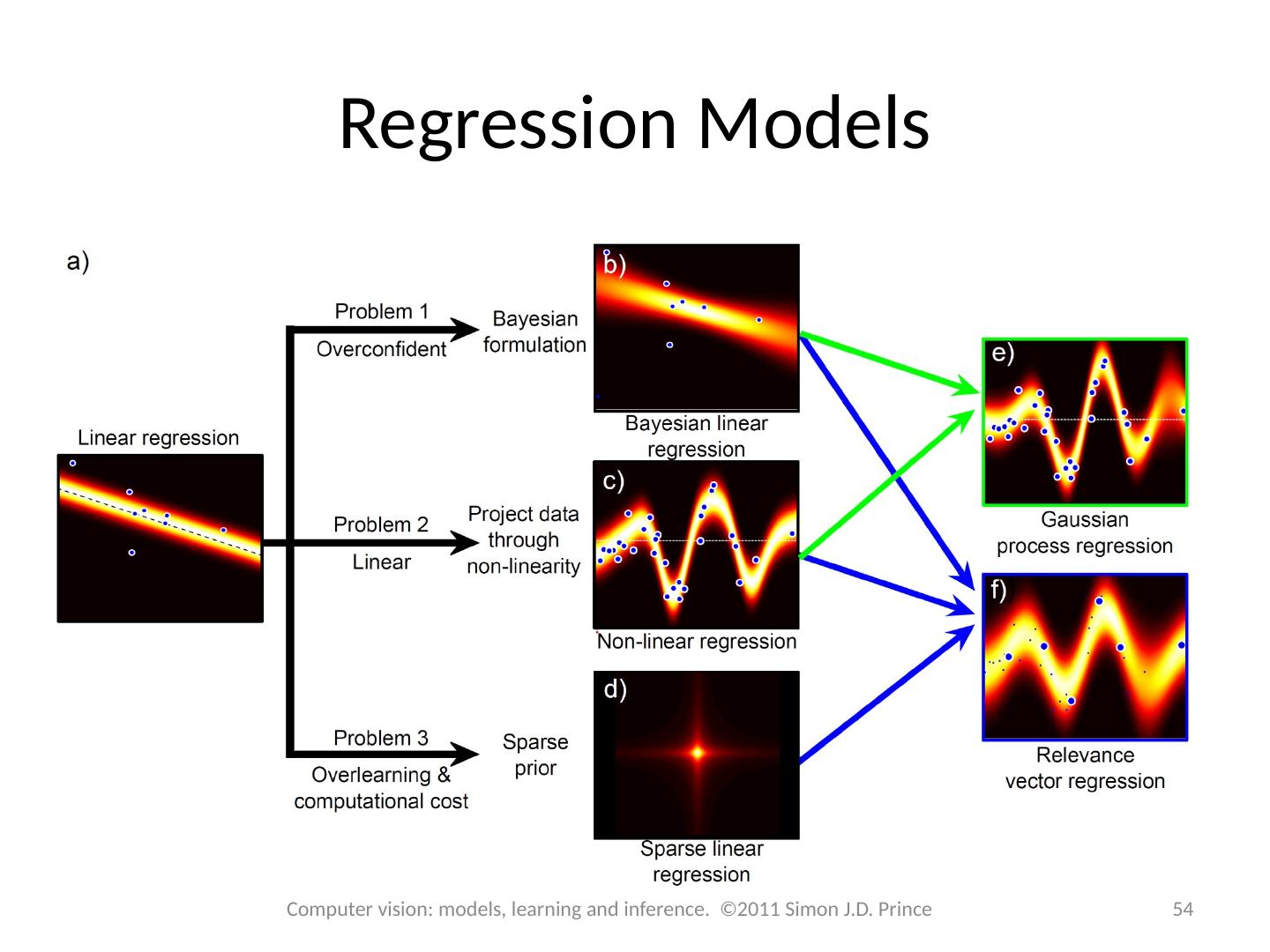
12 .Regression Models 12 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince

13 .Structure 13 13 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince Linear regression Bayesian solution Non-linear regression Kernelization and Gaussian processes Sparse linear regression Dual linear regression Relevance vector regression Applications

14 .Bayesian Regression Likelihood Prior (We concentrate on f – come back to s 2 later!) Bayes rule’ 14 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince

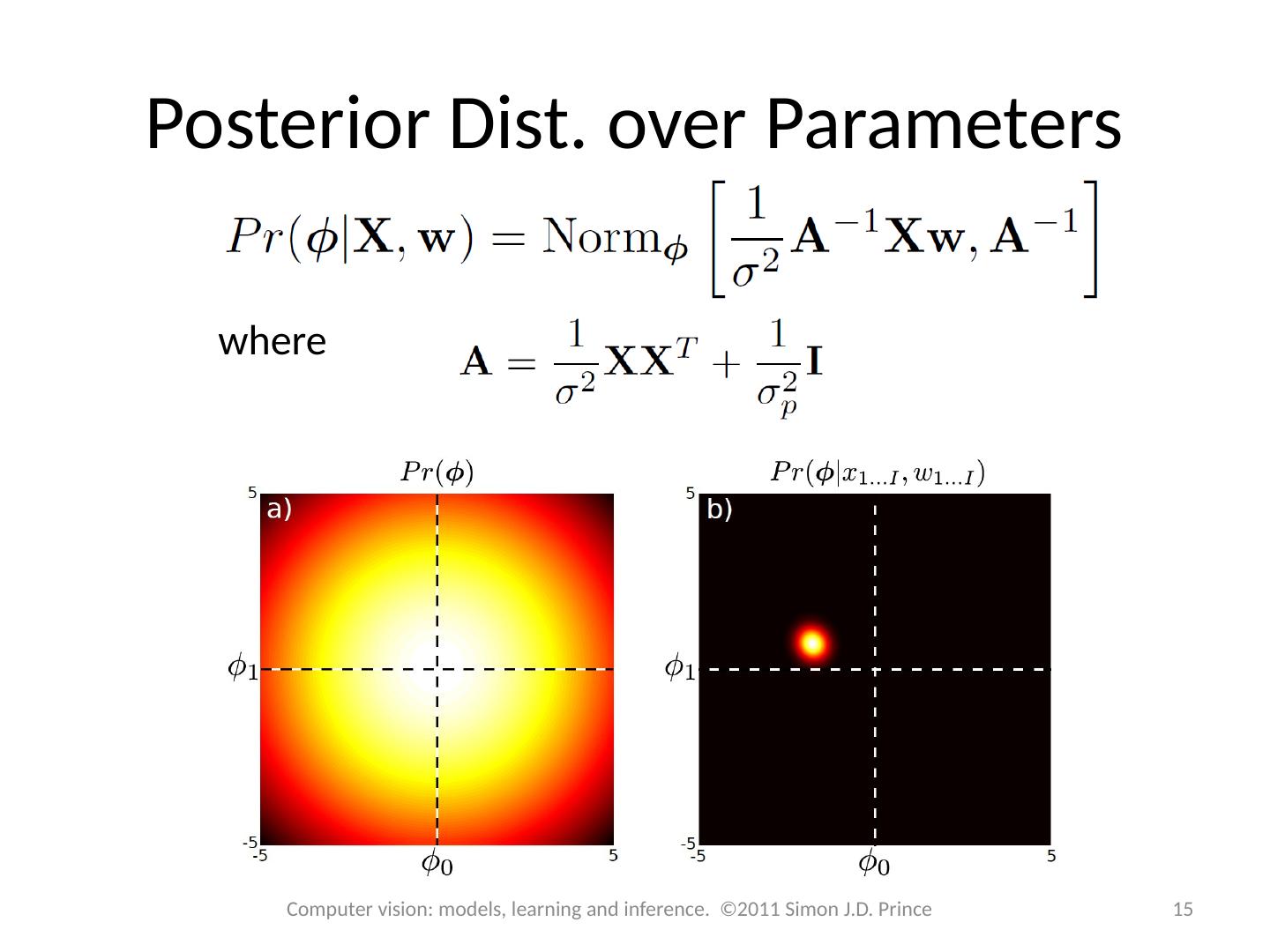
15 .Posterior Dist. over Parameters where 15 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince

16 .Inference 16 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince

17 .Practical Issue Problem: In high dimensions, the matrix A may be too big to invert Solution: Re-express using Matrix Inversion Lemma 17 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince Final expression: inverses are (I x I) , not (D x D)

18 .Fitting Variance We’ll fit the variance with maximum likelihood Optimize the marginal likelihood (likelihood after gradients have been integrated out) 18 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince

19 .Structure 19 19 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince Linear regression Bayesian solution Non-linear regression Kernelization and Gaussian processes Sparse linear regression Dual linear regression Relevance vector regression Applications

20 .Regression Models 20 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince

21 .Non-Linear Regression GOAL: Keep the math of linear regression, but extend to more general functions KEY IDEA: You can make a non-linear function from a linear weighted sum of non-linear basis functions 21 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince

22 .Non-linear regression Linear regression: Non-Linear regression: where In other words, create z by evaluating x against basis functions, then linearly regress against z. 22 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince

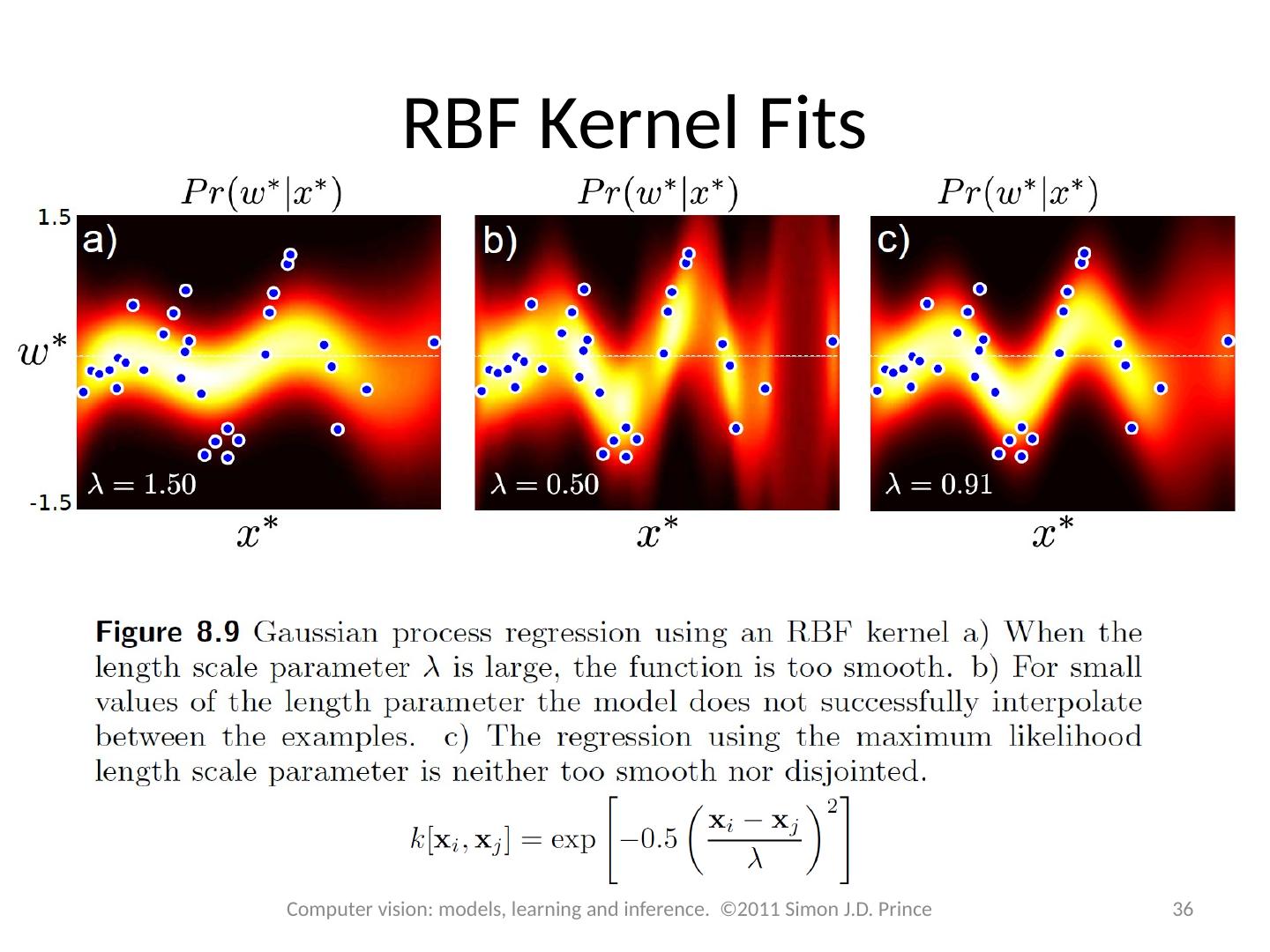
23 .Example: polynomial regression 23 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince A special case of Where

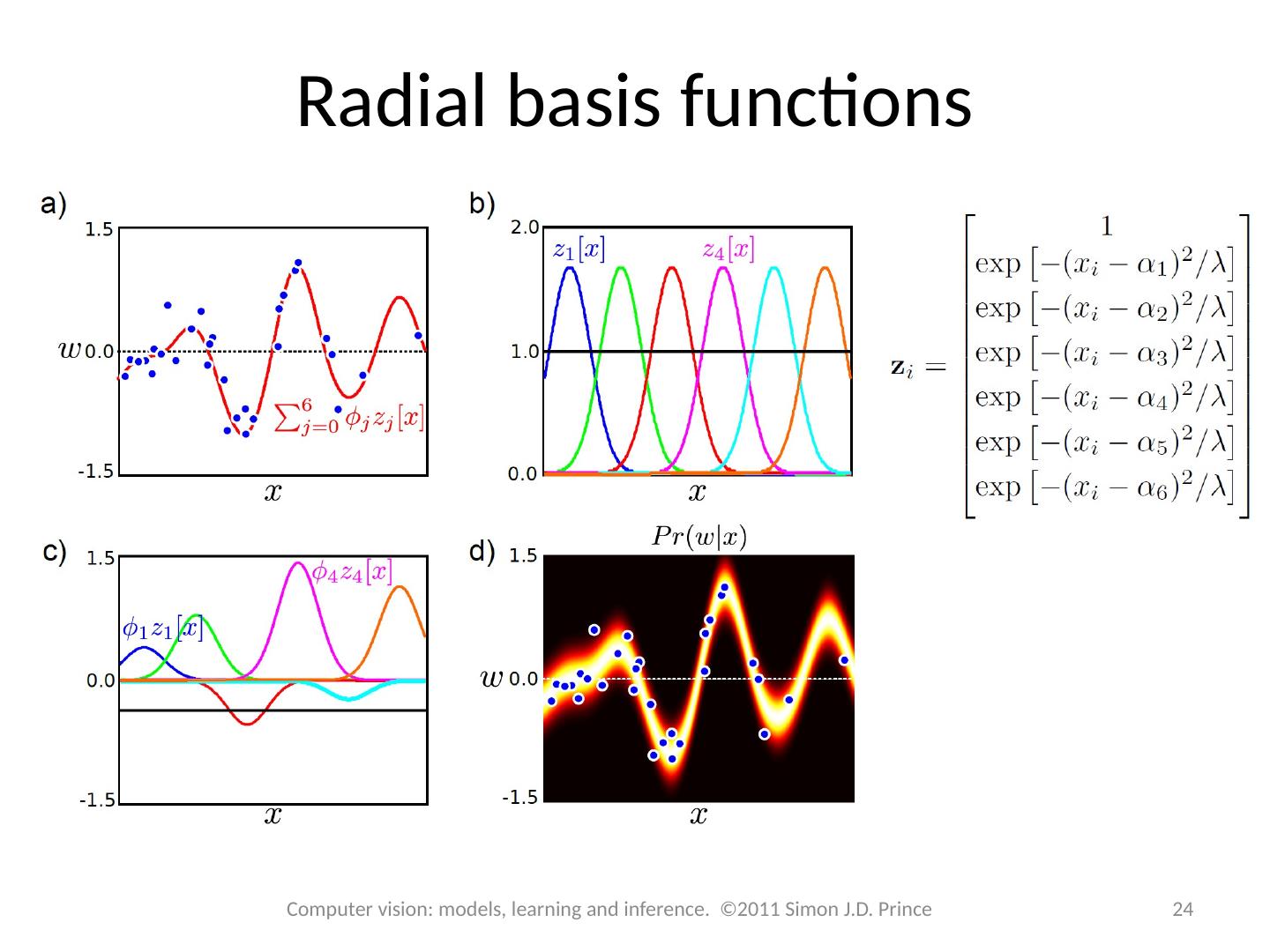
24 .Radial basis functions 24 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince

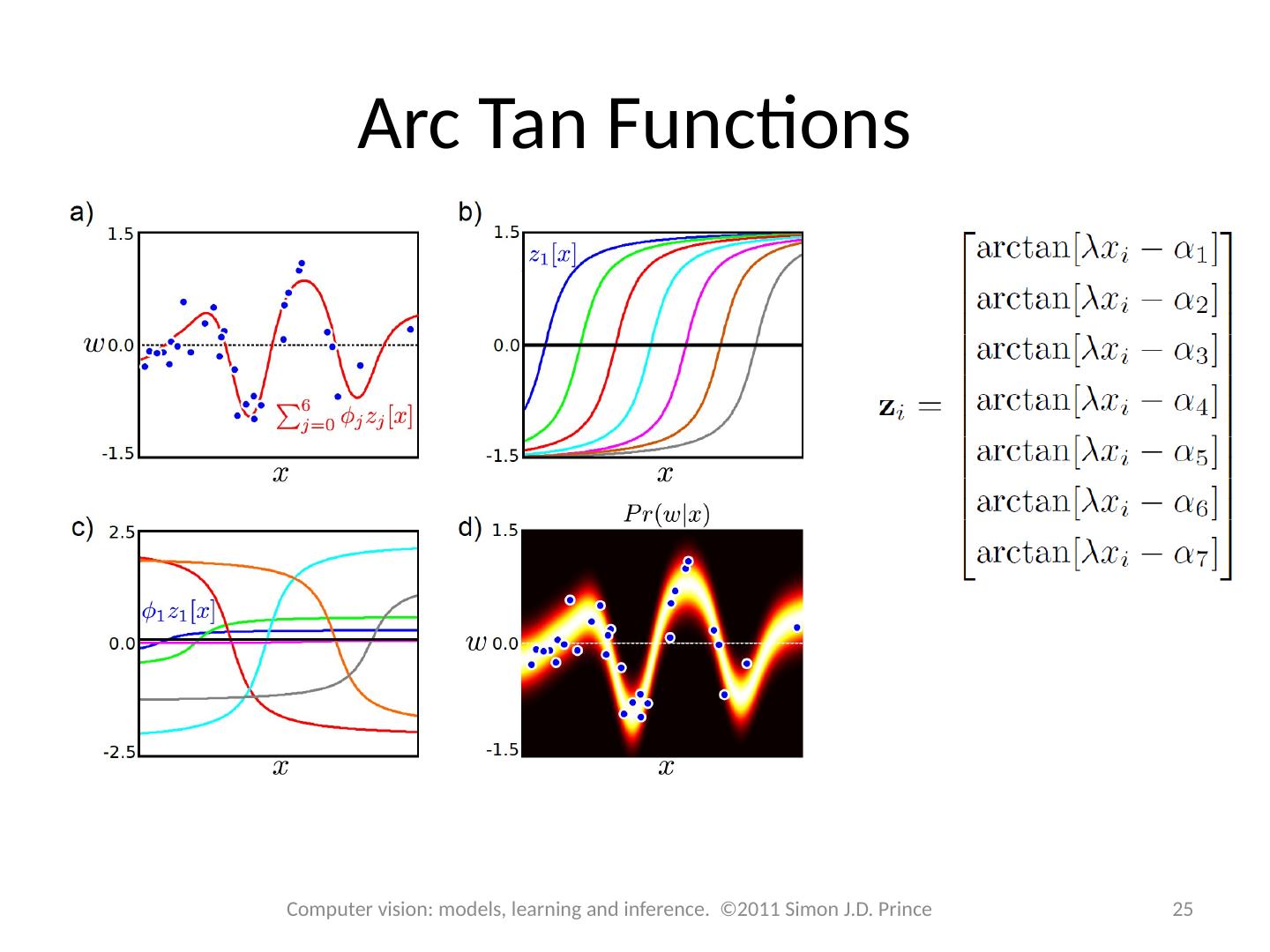
25 .Arc Tan Functions 25 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince

26 .Non-linear regression Linear regression: Non-Linear regression: where In other words, create z by evaluating x against basis functions, then linearly regress against z. 26 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince

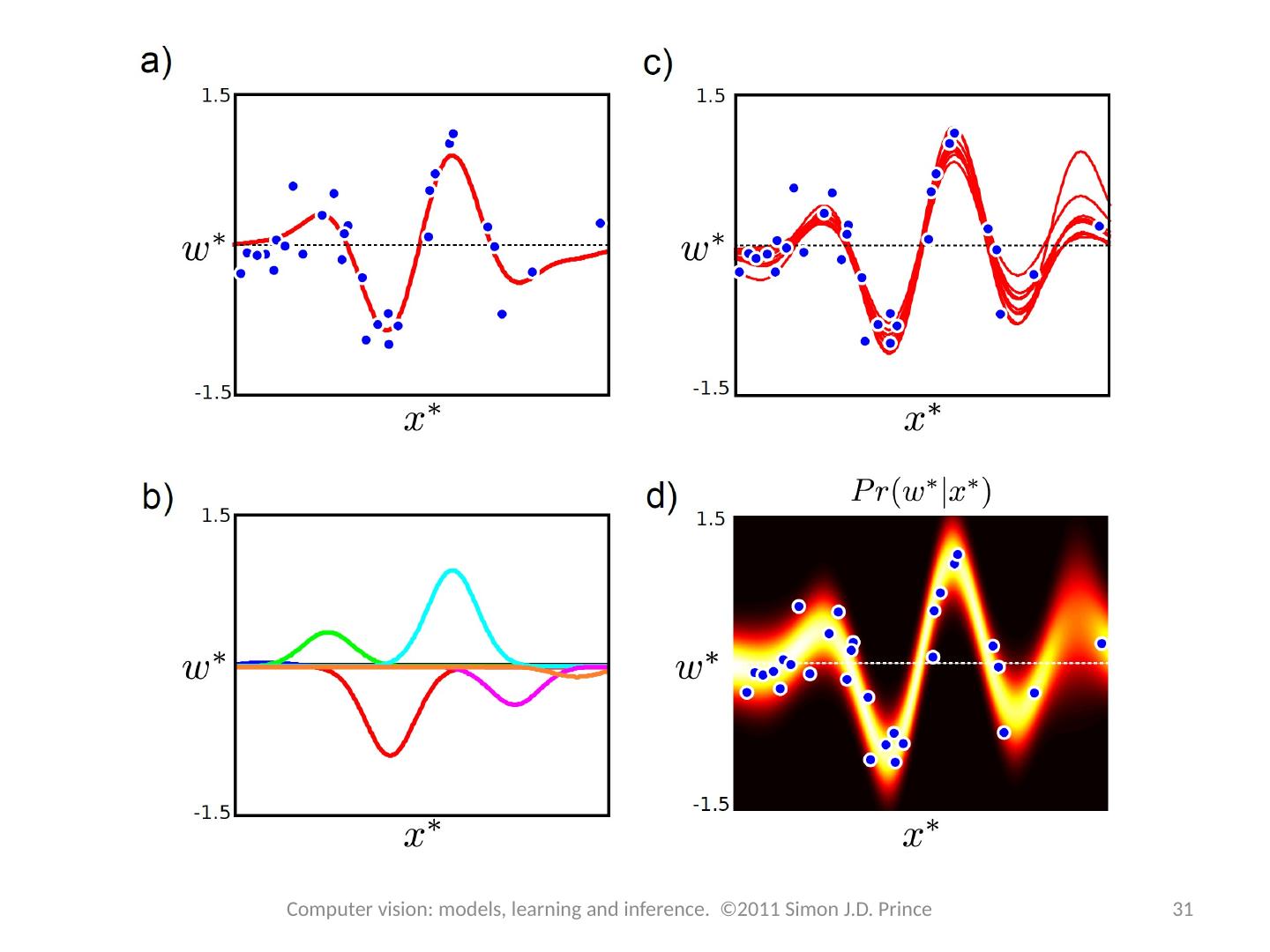
27 .Maximum Likelihood 27 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince Same as linear regression, but substitute in Z for X :

28 .Structure 28 28 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince Linear regression Bayesian solution Non-linear regression Kernelization and Gaussian processes Sparse linear regression Dual linear regression Relevance vector regression Applications

29 .Regression Models 29 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince