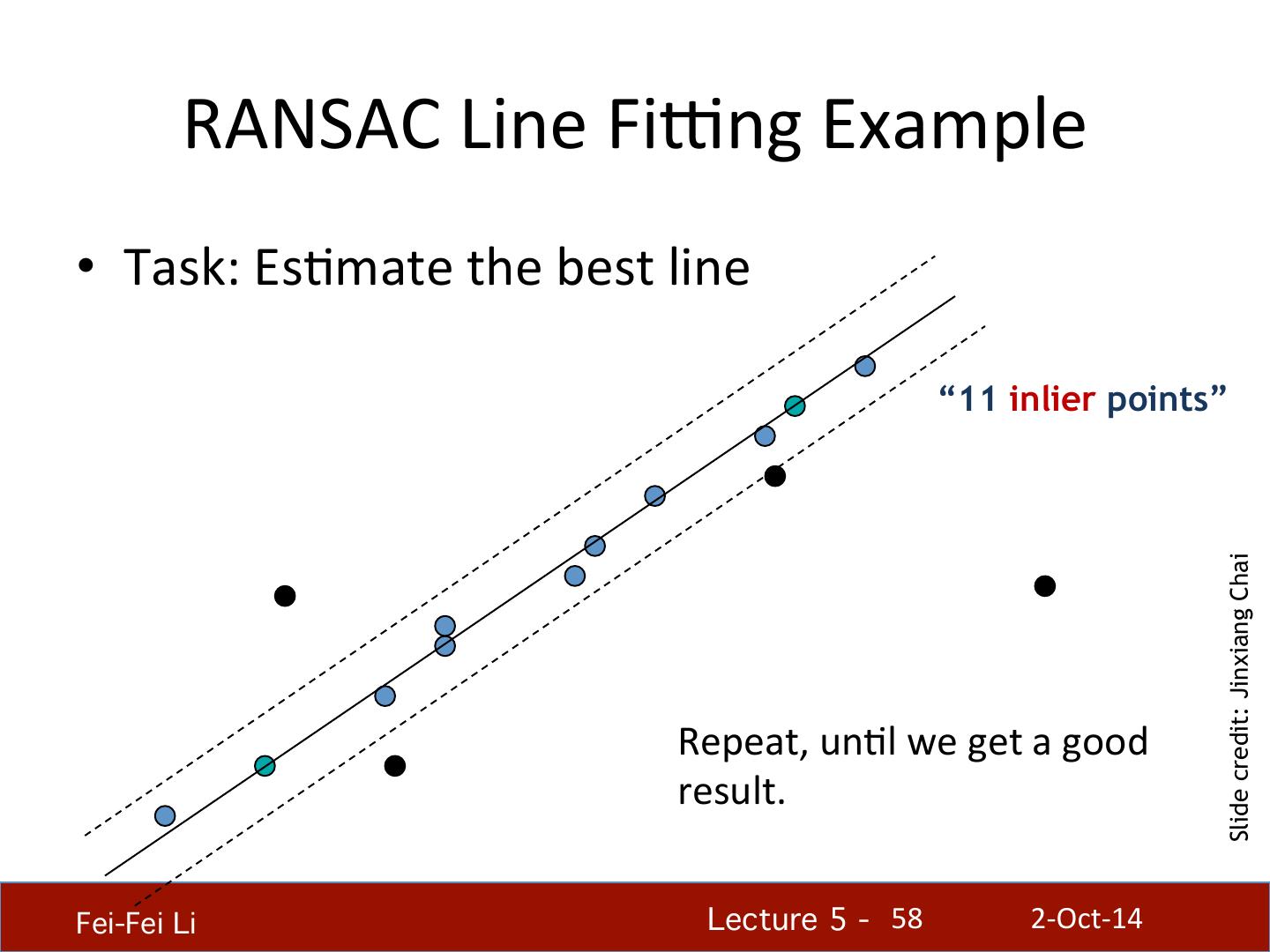
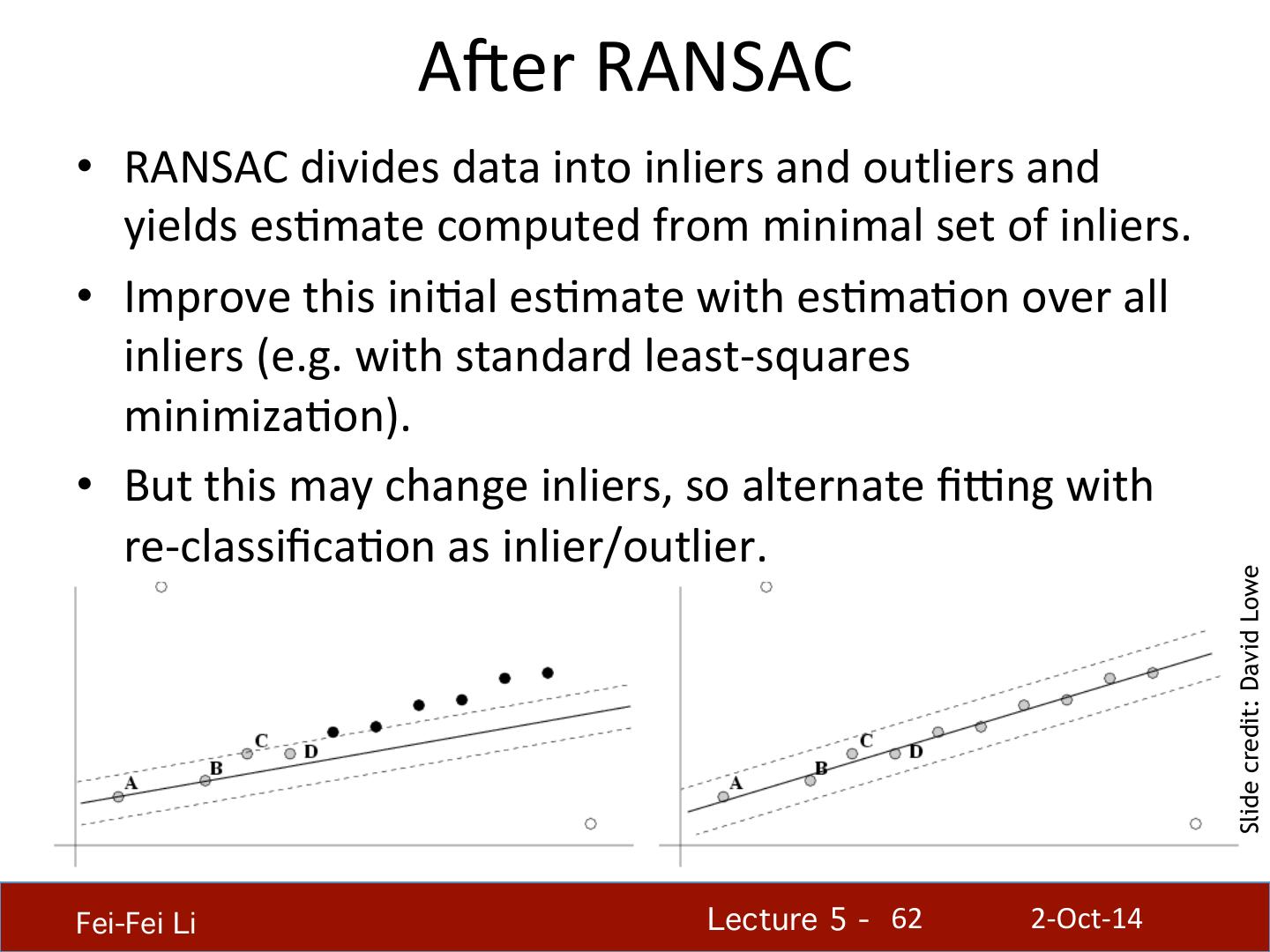
- 快召唤伙伴们来围观吧
- 微博 QQ QQ空间 贴吧
- 文档嵌入链接
- <iframe src="https://www.slidestalk.com/u231/edge_detection_computer?embed" frame border="0" width="640" height="360" scrolling="no" allowfullscreen="true">复制
- 微信扫一扫分享
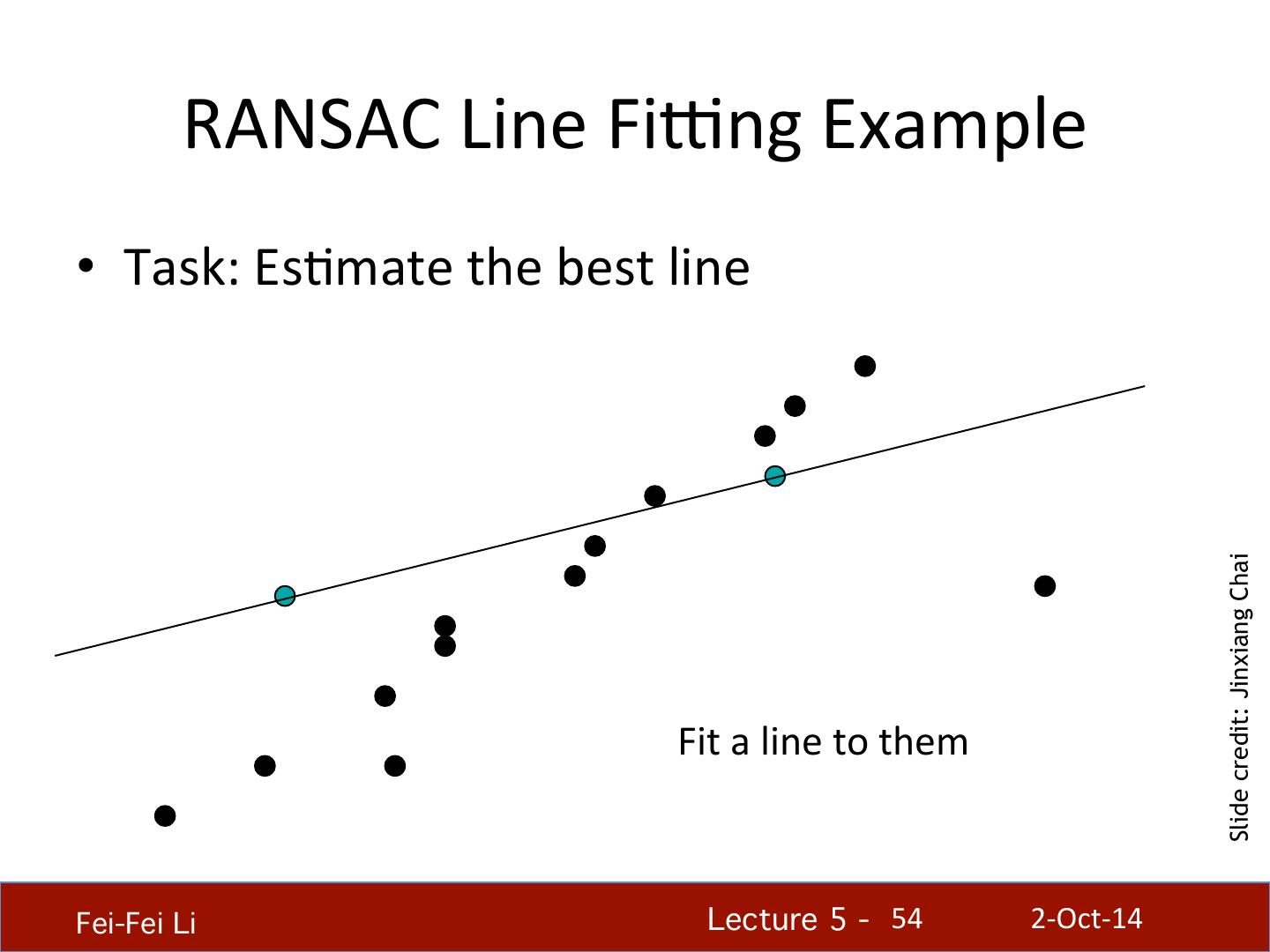
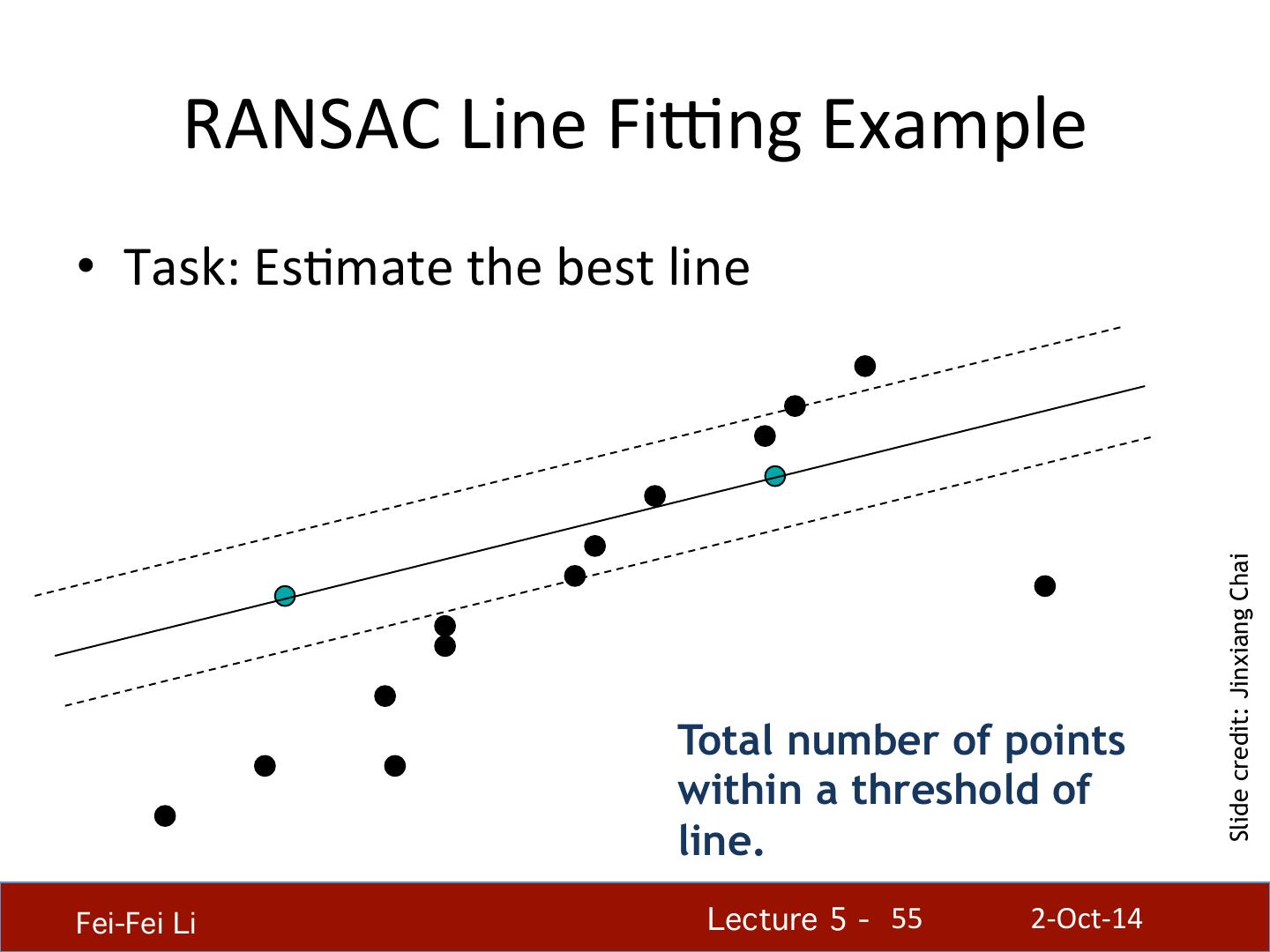
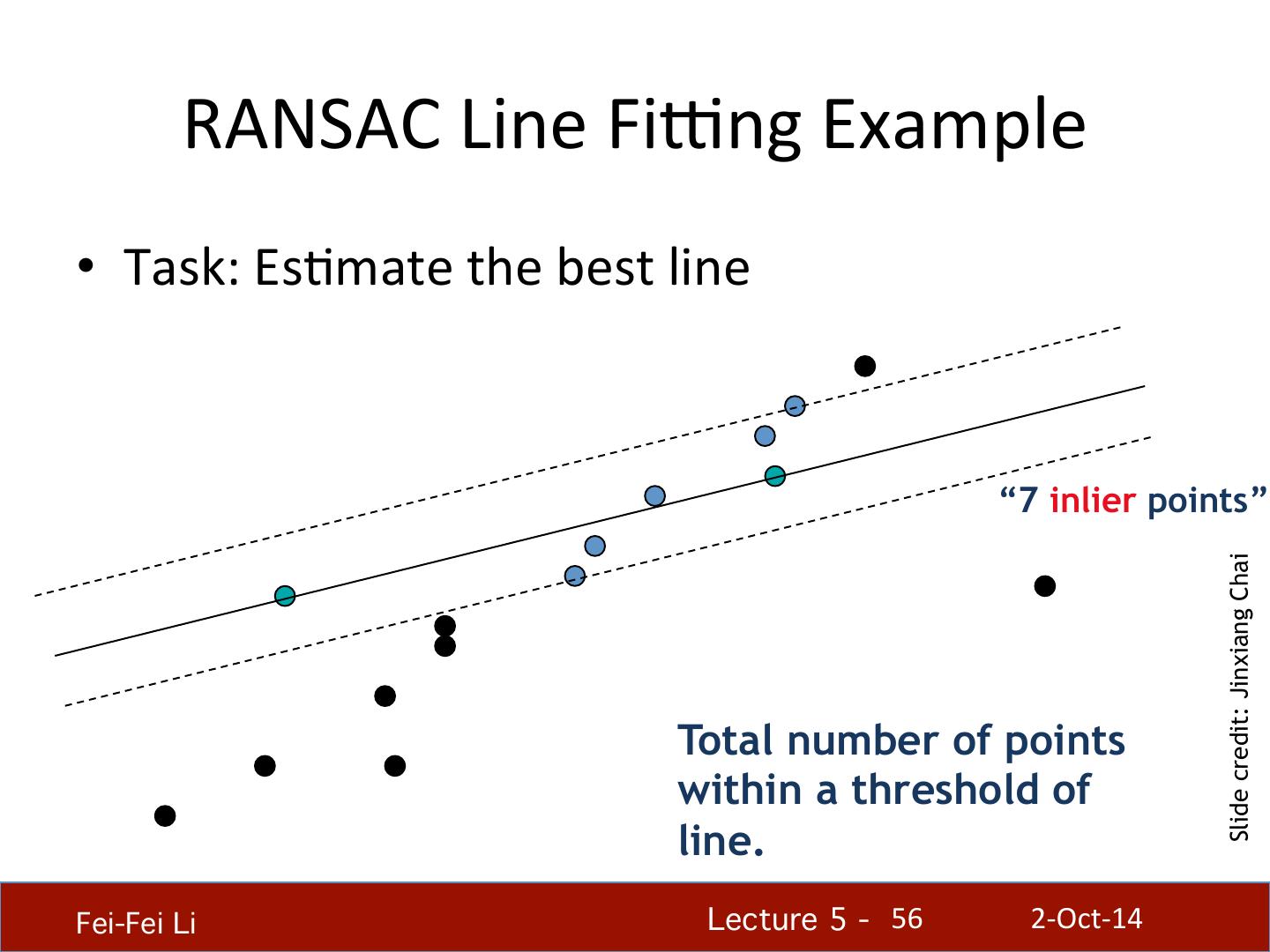
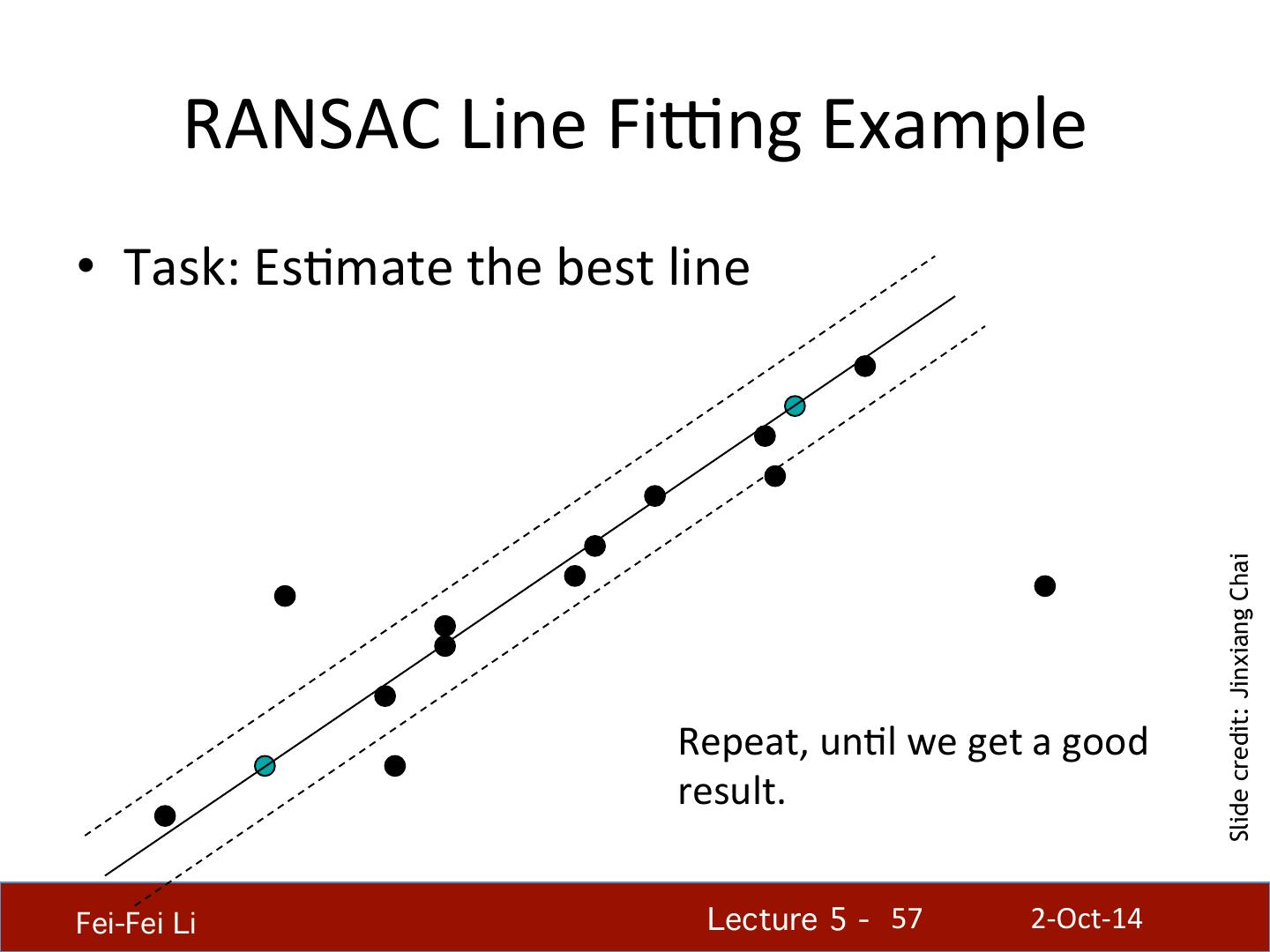
Edge Detection
展开查看详情
1 . Lecture 5: Edge Detec.on Professor Fei-‐Fei Li Stanford Vision Lab Fei-Fei Li! Lecture 5 - !1 2-‐Oct-‐14
2 . What we will learn today • Edge detec.on • A simple edge detector • Canny edge detector • A model fiIng method for edge detec.on – RANSAC Some background reading: Forsyth and Ponce, Computer Vision, Chapter 8, Chapter 15.5.2 Fei-Fei Li! Lecture 5 - !2 2-‐Oct-‐14
3 . (A) Cave pain.ng at Chauvet, France, about 30,000 B.C.; (B) Aerial photograph of the picture of a monkey as part of the Nazca Lines geoplyphs, Peru, about 700 – 200 B.C.; (C) Shen Zhou (1427-‐1509 A.D.): Poet on a mountain top, ink on paper, China; (D) Line drawing by 7-‐year old I. Lleras (2010 A.D.). Fei-Fei Li! Lecture 5 - !3 2-‐Oct-‐14
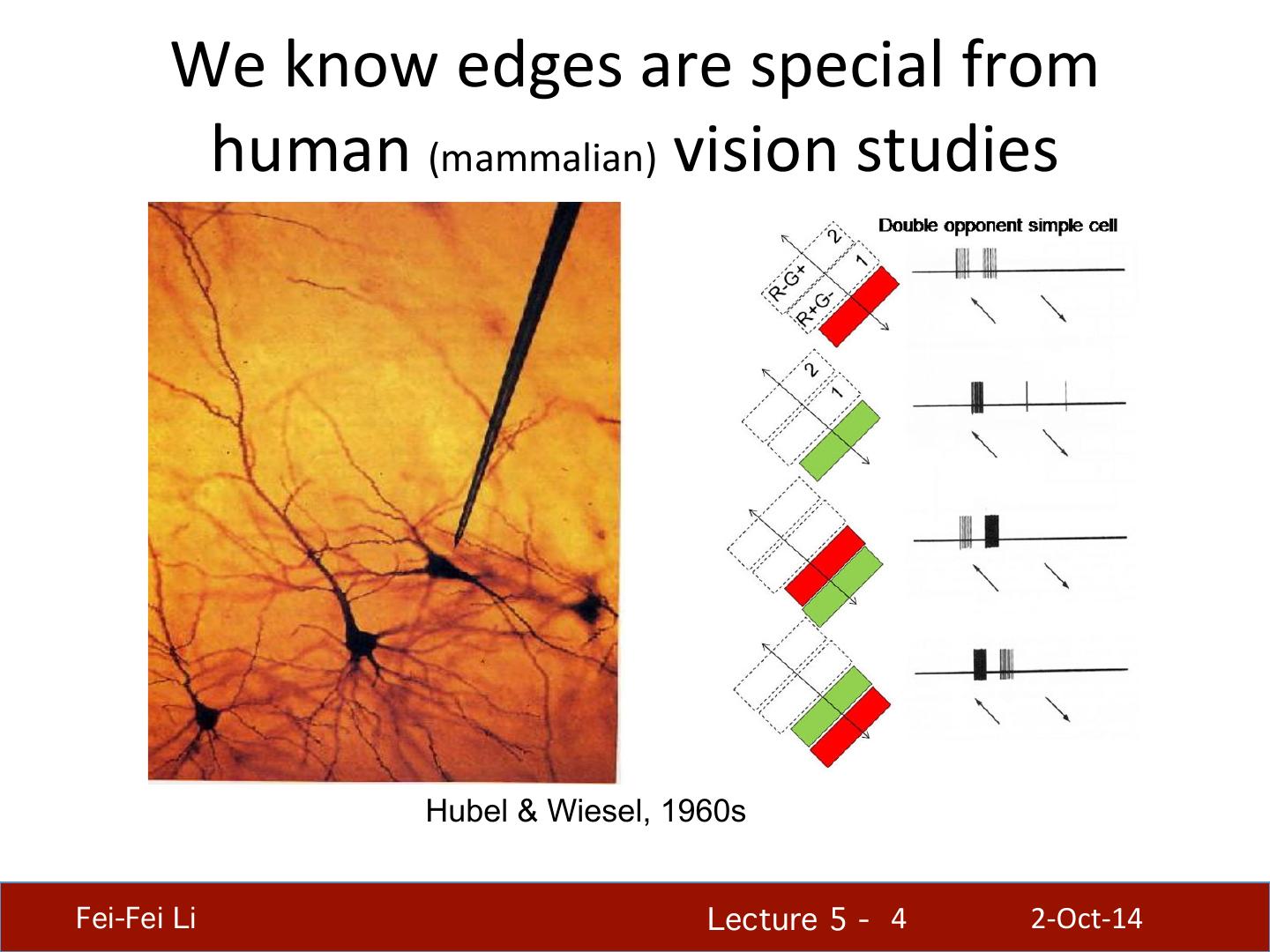
4 . We know edges are special from human (mammalian) vision studies Hubel & Wiesel, 1960s Fei-Fei Li! Lecture 5 - !4 2-‐Oct-‐14
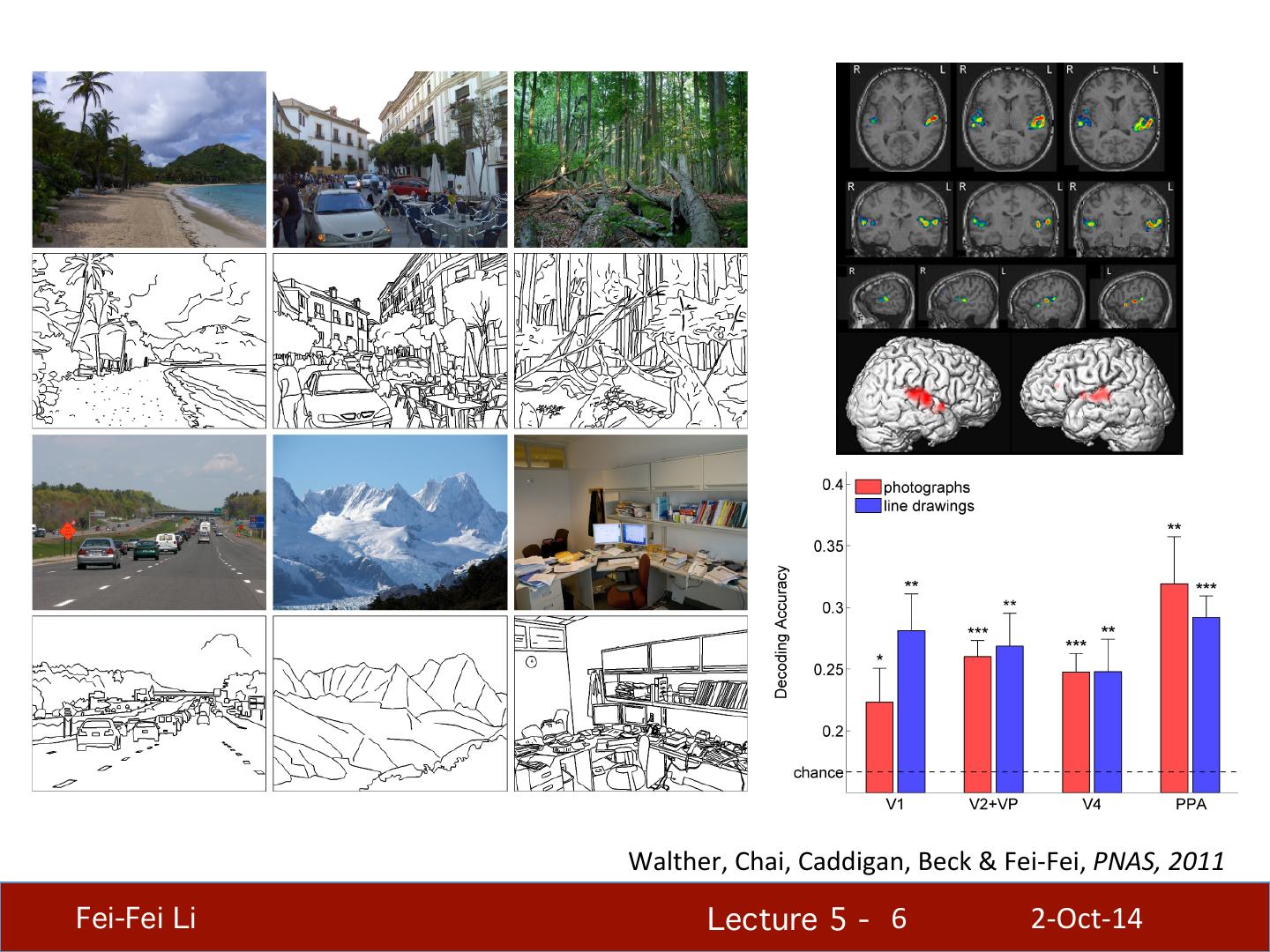
5 . We know edges are special from human (mammalian) vision studies Fei-Fei Li! Lecture 5 - !5 2-‐Oct-‐14
6 . Walther, Chai, Caddigan, Beck & Fei-‐Fei, PNAS, 2011 Fei-Fei Li! Lecture 5 - !6 2-‐Oct-‐14
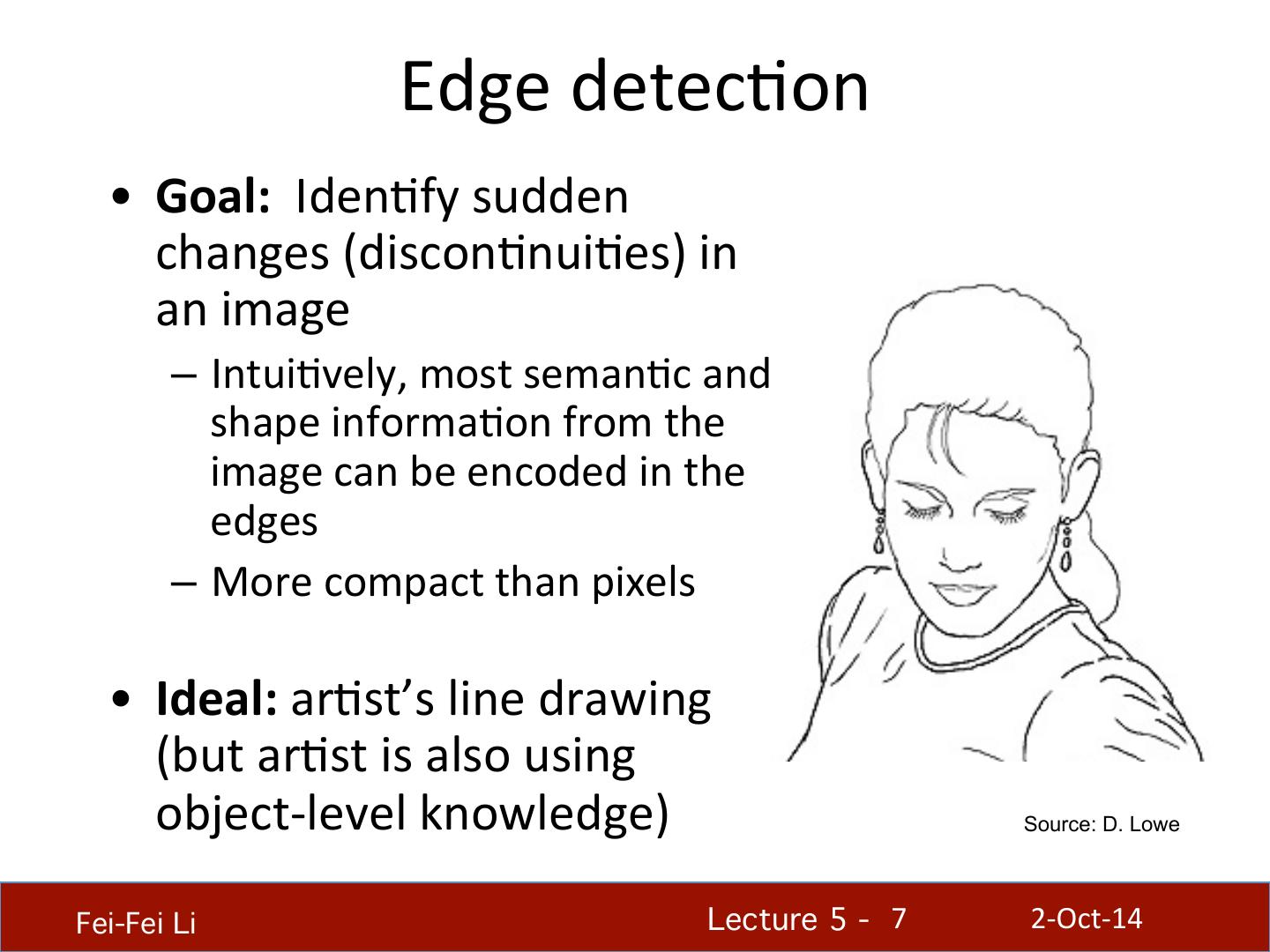
7 . Edge detec.on • Goal: Iden.fy sudden changes (discon.nui.es) in an image – Intui.vely, most seman.c and shape informa.on from the image can be encoded in the edges – More compact than pixels • Ideal: ar.st’s line drawing (but ar.st is also using object-‐level knowledge) Source: D. Lowe Fei-Fei Li! Lecture 5 - !7 2-‐Oct-‐14
8 . Why do we care about edges? • Extract informa.on, recognize objects • Recover geometry and Vertical vanishing point (at infinity) Vanishing viewpoint line Vanishing Vanishing point point Source: J. Hayes Fei-Fei Li! Lecture 5 - !8 2-‐Oct-‐14
9 . Origins of edges surface normal discontinuity depth discontinuity surface color discontinuity illumination discontinuity Source: D. Hoiem Fei-Fei Li! Lecture 5 - !9 2-‐Oct-‐14
10 . Closeup of edges Surface normal discon.nuity Source: D. Hoiem Fei-Fei Li! Lecture 5 - !10 2-‐Oct-‐14
11 . Closeup of edges Depth discon.nuity Source: D. Hoiem Fei-Fei Li! Lecture 5 - !11 2-‐Oct-‐14
12 . Closeup of edges Surface color discon.nuity Source: D. Hoiem Fei-Fei Li! Lecture 5 - !12 2-‐Oct-‐14
13 . What we will learn today • Edge detec.on • A simple edge detector • Canny edge detector • A model fiIng method for edge detec.on – RANSAC Fei-Fei Li! Lecture 5 - !13 2-‐Oct-‐14
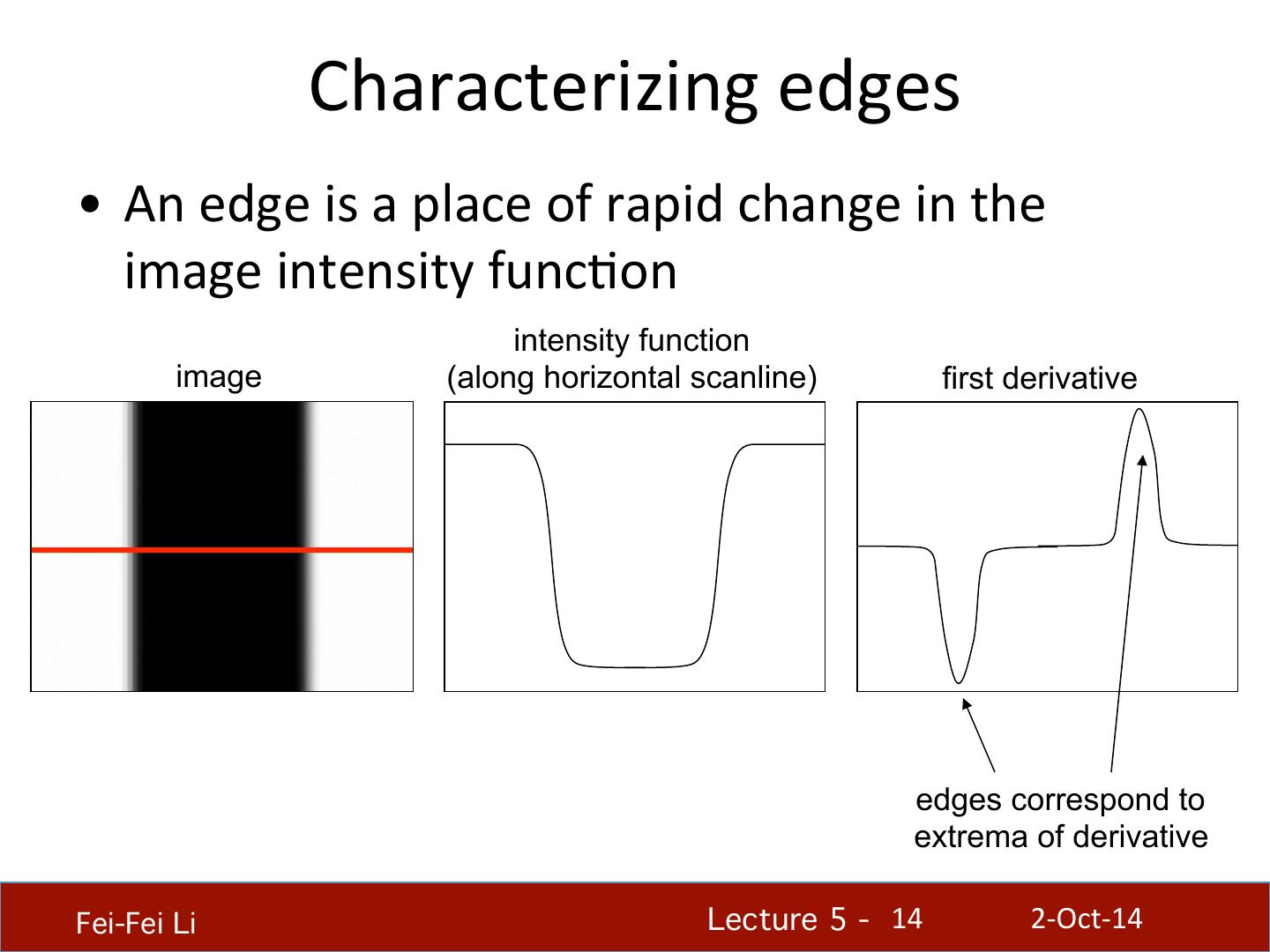
14 . Characterizing edges • An edge is a place of rapid change in the image intensity func.on intensity function image (along horizontal scanline) first derivative edges correspond to extrema of derivative Fei-Fei Li! Lecture 5 - !14 2-‐Oct-‐14
15 . Image gradient • The gradient of an image: The gradient points in the direc.on of most rapid increase in intensity The gradient direc.on is given by • how does this relate to the direc.on of the edge? The edge strength is given by the gradient magnitude Source: Steve Seitz Fei-Fei Li! Lecture 5 - !15 2-‐Oct-‐14
16 . Finite differences: example • Which one is the gradient in the x-‐direc.on? How about y-‐direc.on? Fei-Fei Li! Lecture 5 - !16 2-‐Oct-‐14
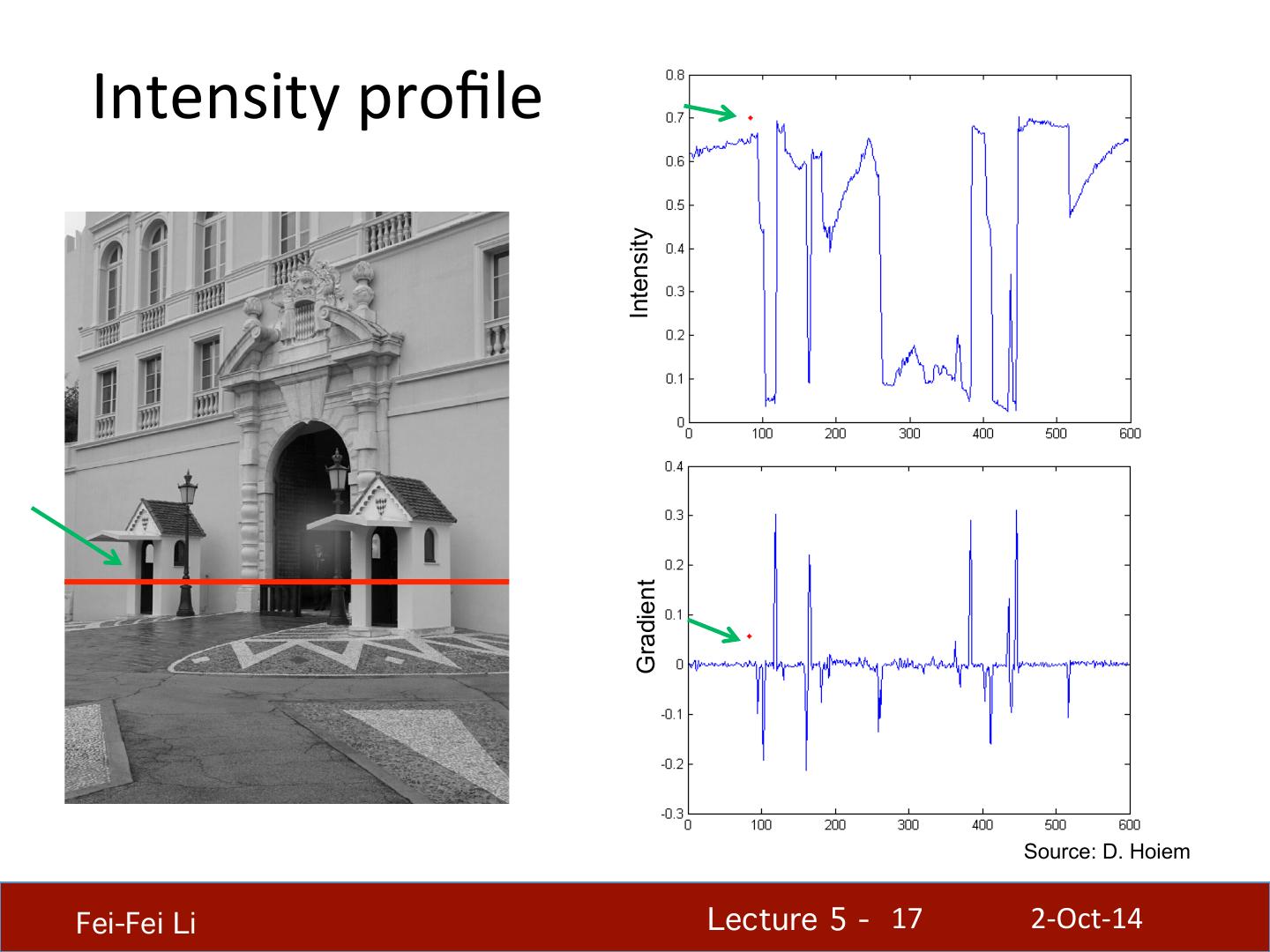
17 . Intensity profile Intensity Gradient Source: D. Hoiem Fei-Fei Li! Lecture 5 - !17 2-‐Oct-‐14
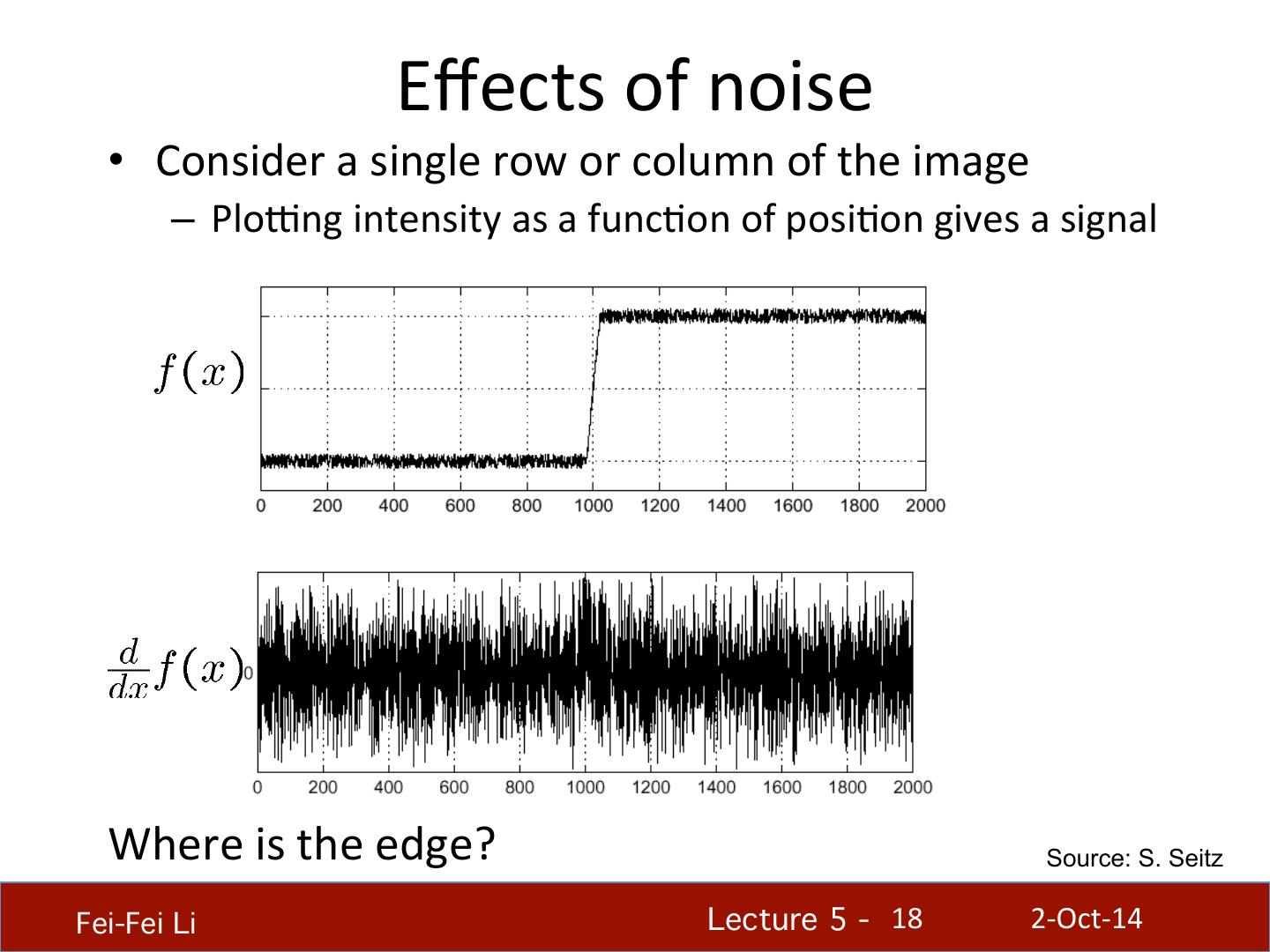
18 . Effects of noise • Consider a single row or column of the image – PloIng intensity as a func.on of posi.on gives a signal Where is the edge? Source: S. Seitz Fei-Fei Li! Lecture 5 - !18 2-‐Oct-‐14
19 . Effects of noise • Finite difference filters respond strongly to noise – Image noise results in pixels that look very different from their neighbors – Generally, the larger the noise the stronger the response • What is to be done? – Smoothing the image should help, by forcing pixels different to their neighbors (=noise pixels?) to look more like neighbors Source: D. Forsyth Fei-Fei Li! Lecture 5 - !19 2-‐Oct-‐14
20 . Effects of noise • Finite difference filters respond strongly to noise – Image noise results in pixels that look very different from their neighbors – Generally, the larger the noise the stronger the response • What is to be done? – Smoothing the image should help, by forcing pixels different to their neighbors (=noise pixels?) to look more like neighbors Source: D. Forsyth Fei-Fei Li! Lecture 5 - !20 2-‐Oct-‐14
21 . Solu.on: smooth first f g f*g d ( f ∗ g) dx d • To find edges, look for peaks in ( f ∗ g) dx Source: S. Seitz Fei-Fei Li! Lecture 5 - !21 2-‐Oct-‐14
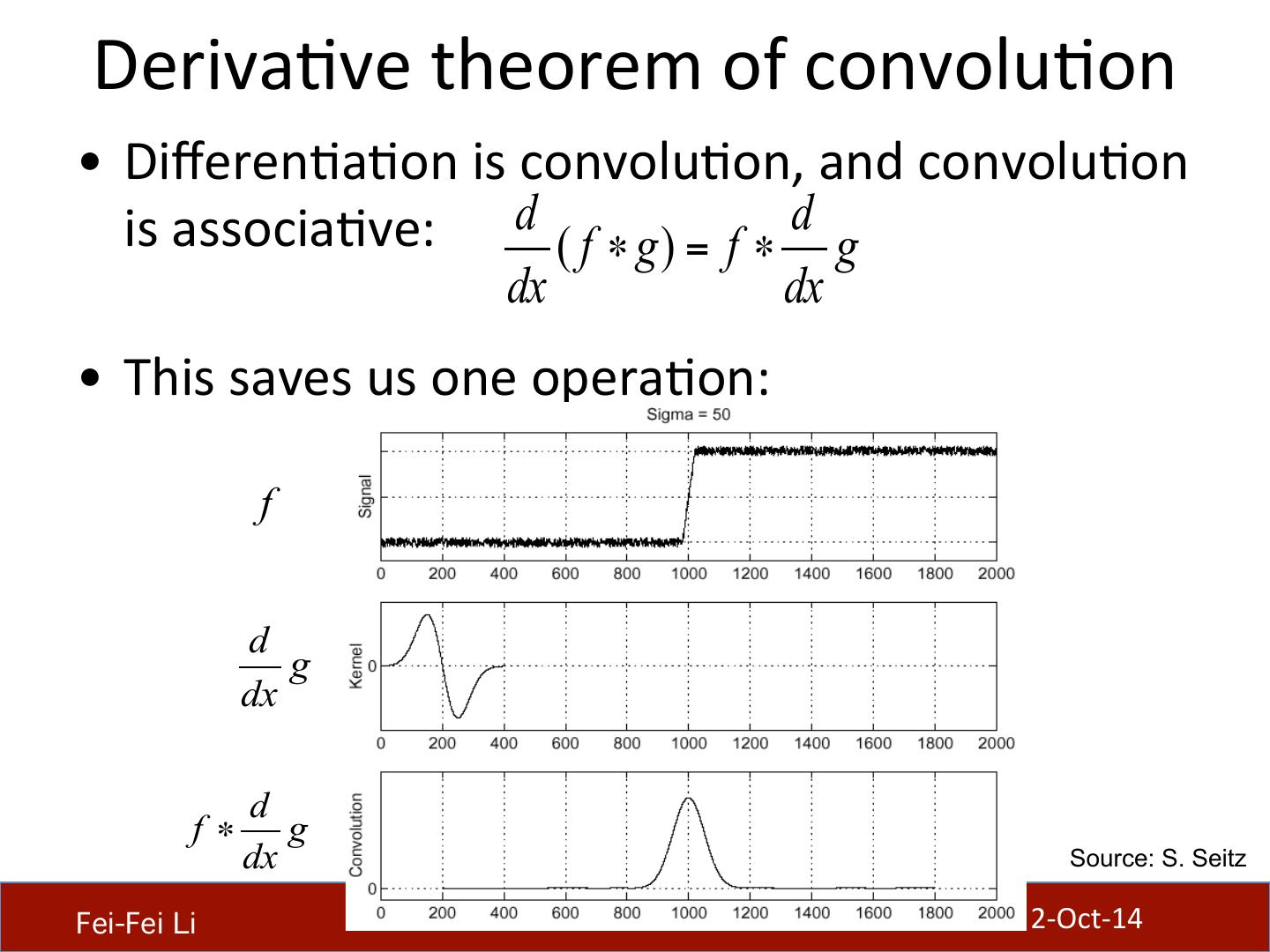
22 . Deriva.ve theorem of convolu.on • Differen.a.on is convolu.on, and convolu.on is associa.ve: d ( f ∗ g ) = f ∗ d g dx dx • This saves us one opera.on: f d g dx d f∗ g dx Source: S. Seitz Fei-Fei Li! Lecture 5 - !22 2-‐Oct-‐14
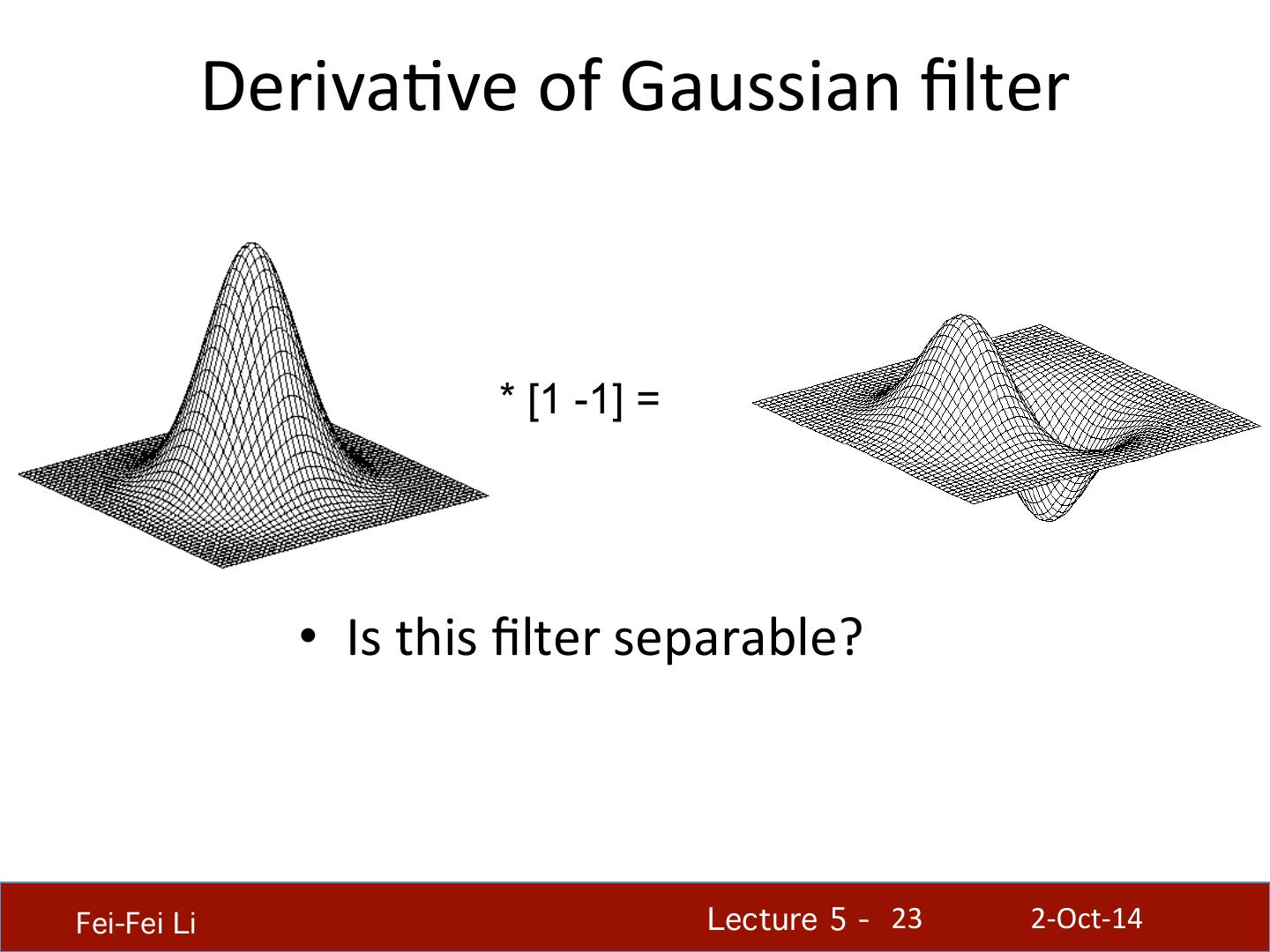
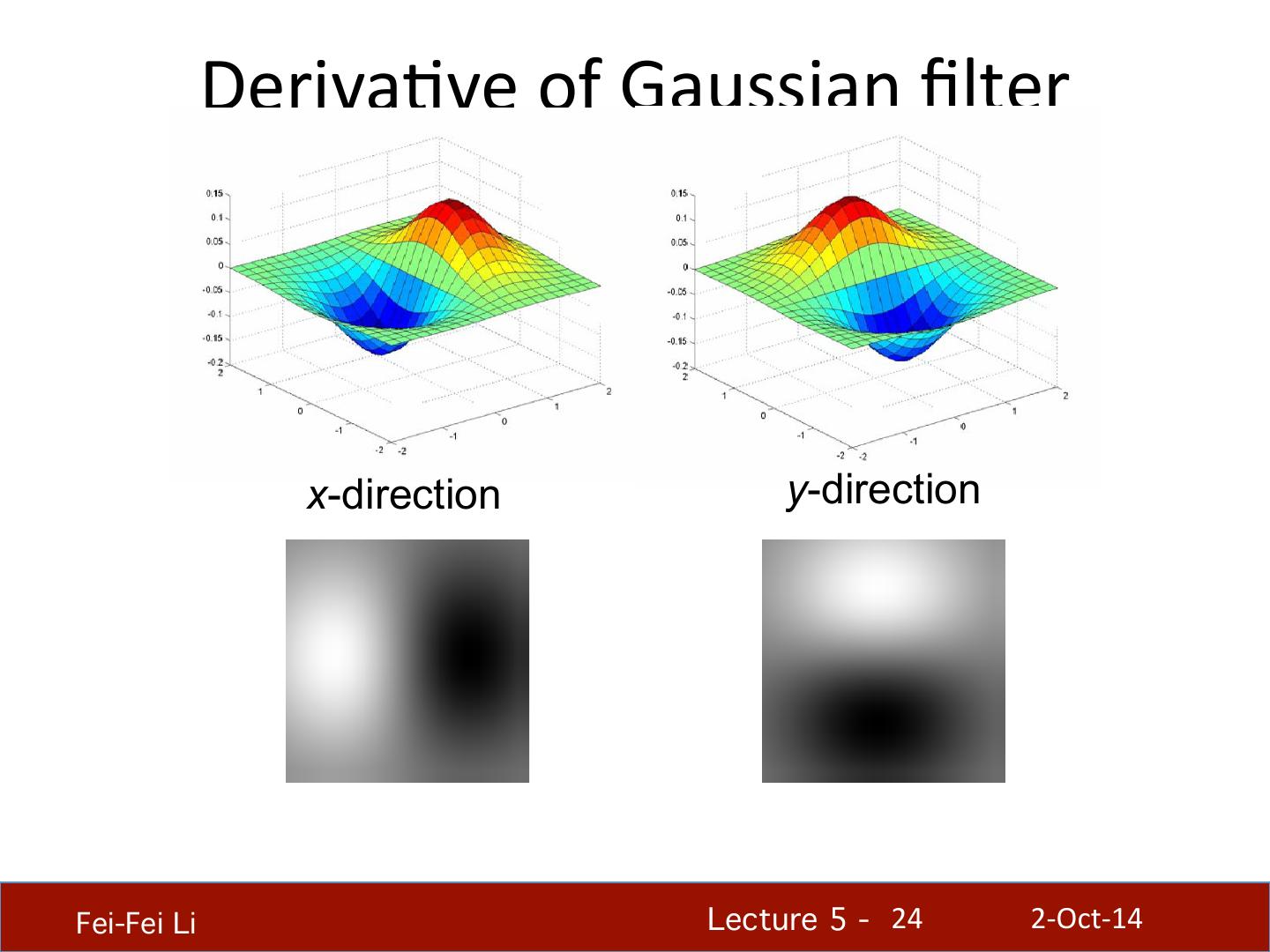
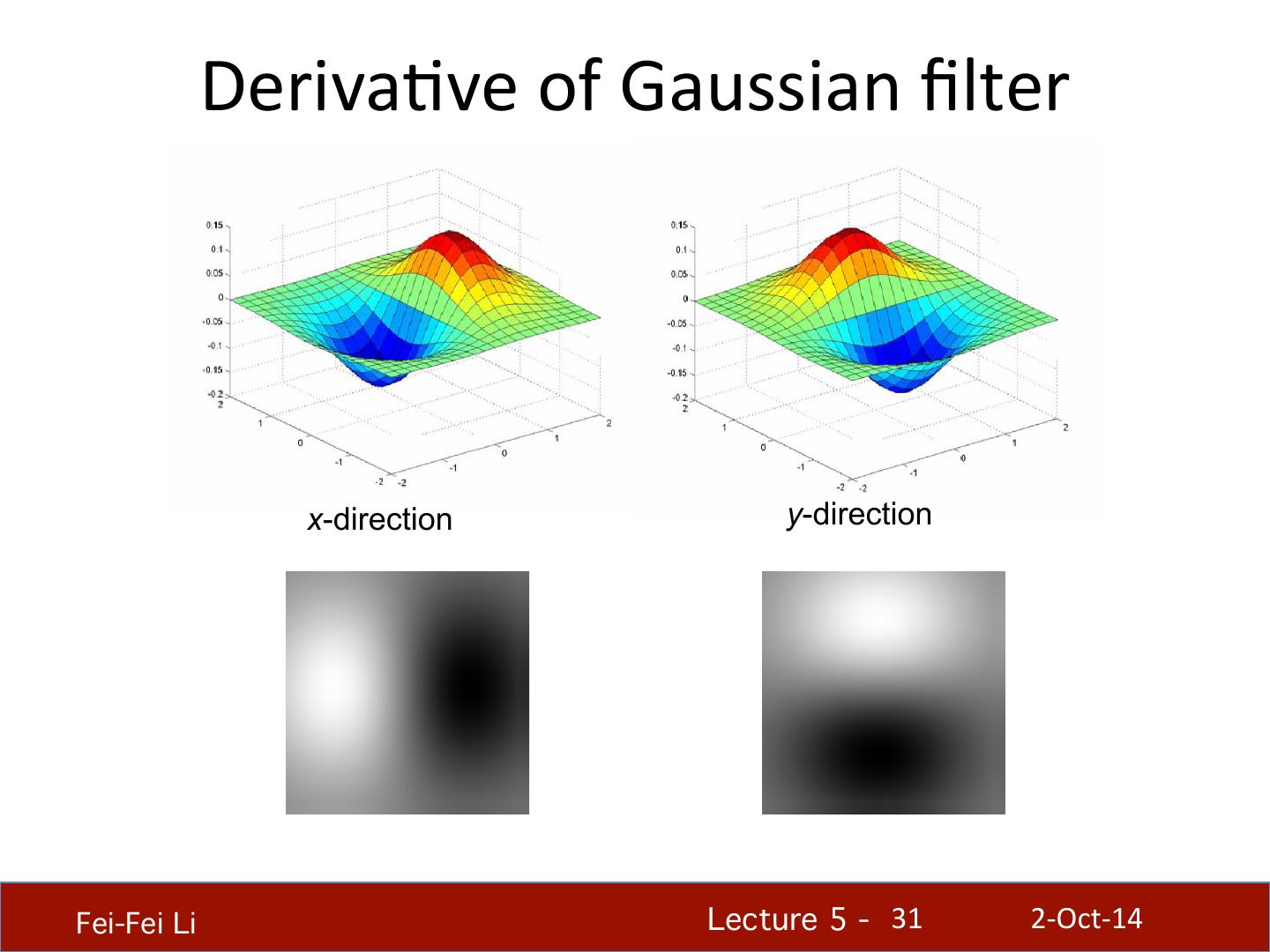
23 . Deriva.ve of Gaussian filter * [1 -1] = • Is this filter separable? Fei-Fei Li! Lecture 5 - !23 2-‐Oct-‐14
24 . Deriva.ve of Gaussian filter x-direction y-direction Fei-Fei Li! Lecture 5 - !24 2-‐Oct-‐14
25 . Tradeoff between smoothing and localiza.on 1 pixel 3 pixels 7 pixels • Smoothed deriva.ve removes noise, but blurs edge. Also finds edges at different “scales”. Source: D. Forsyth Fei-Fei Li! Lecture 5 - !25 2-‐Oct-‐14
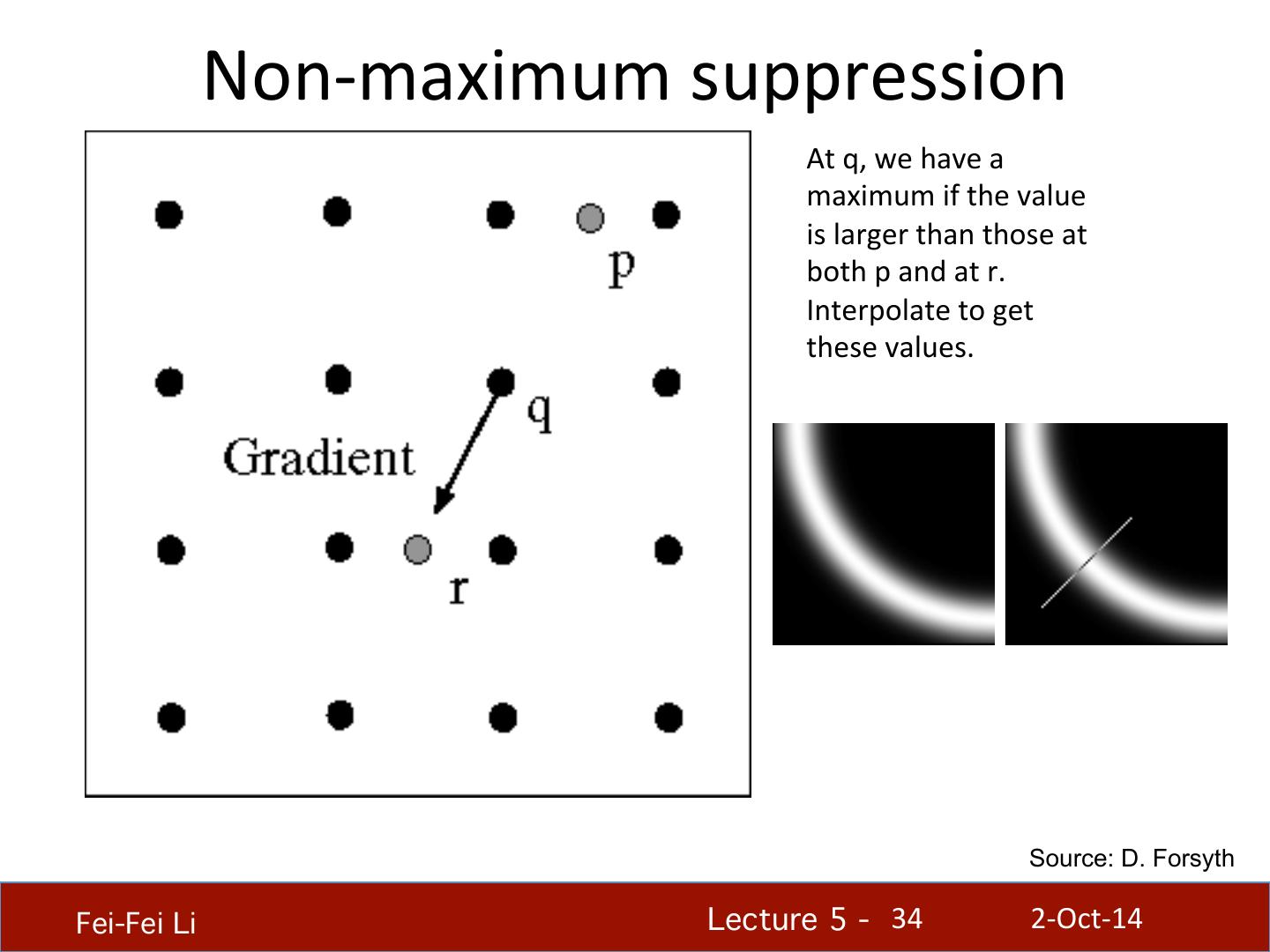
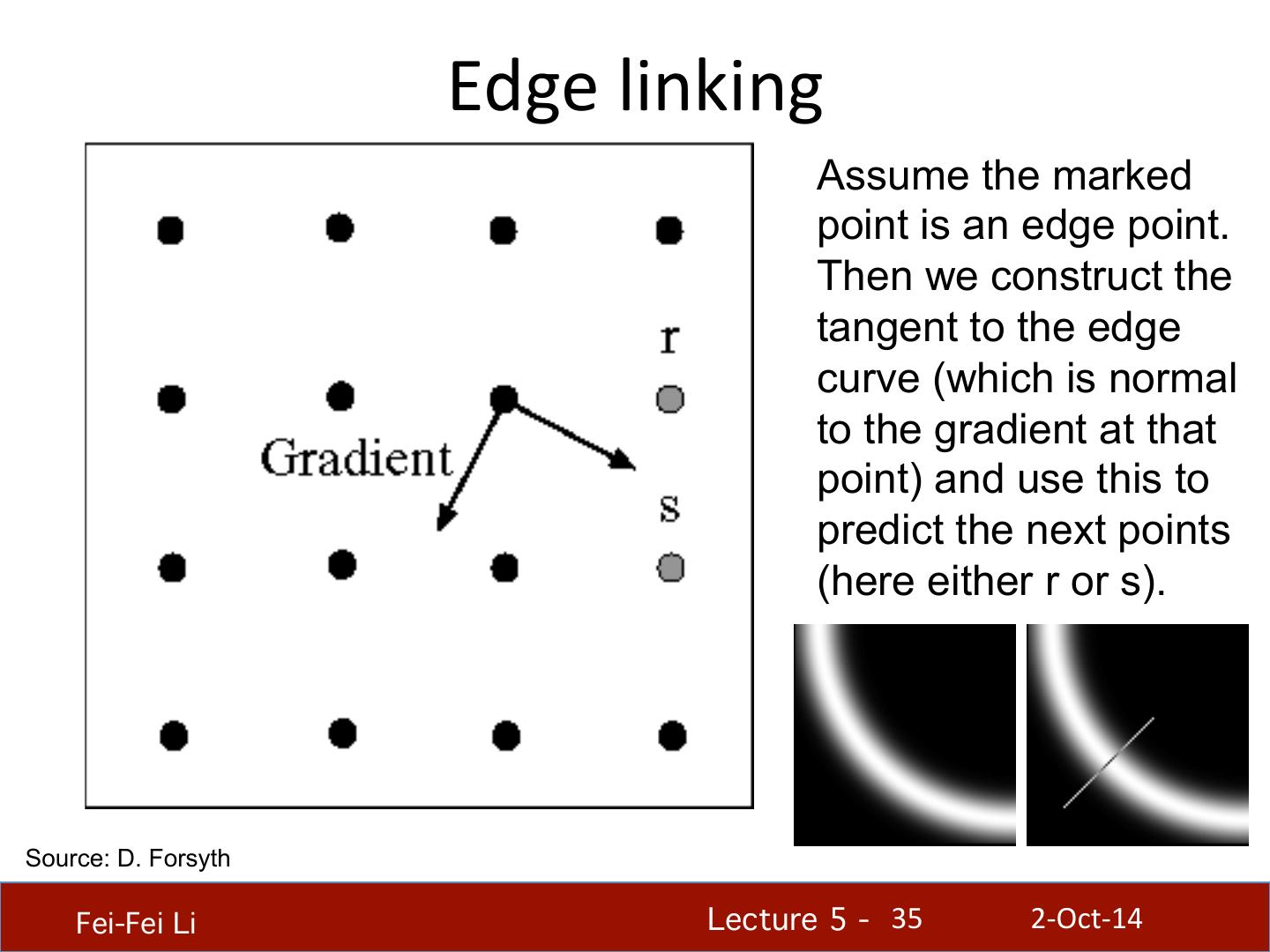
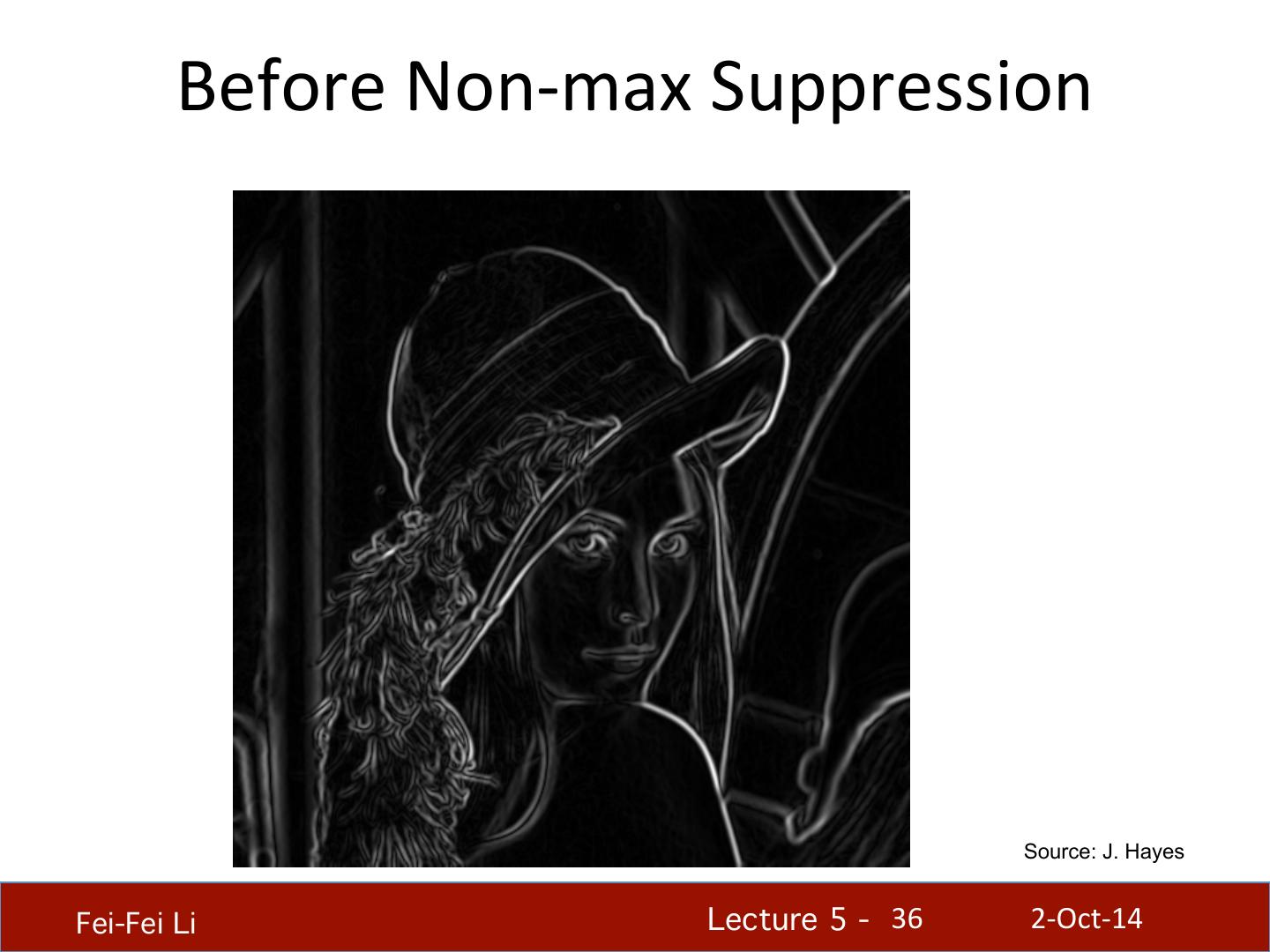
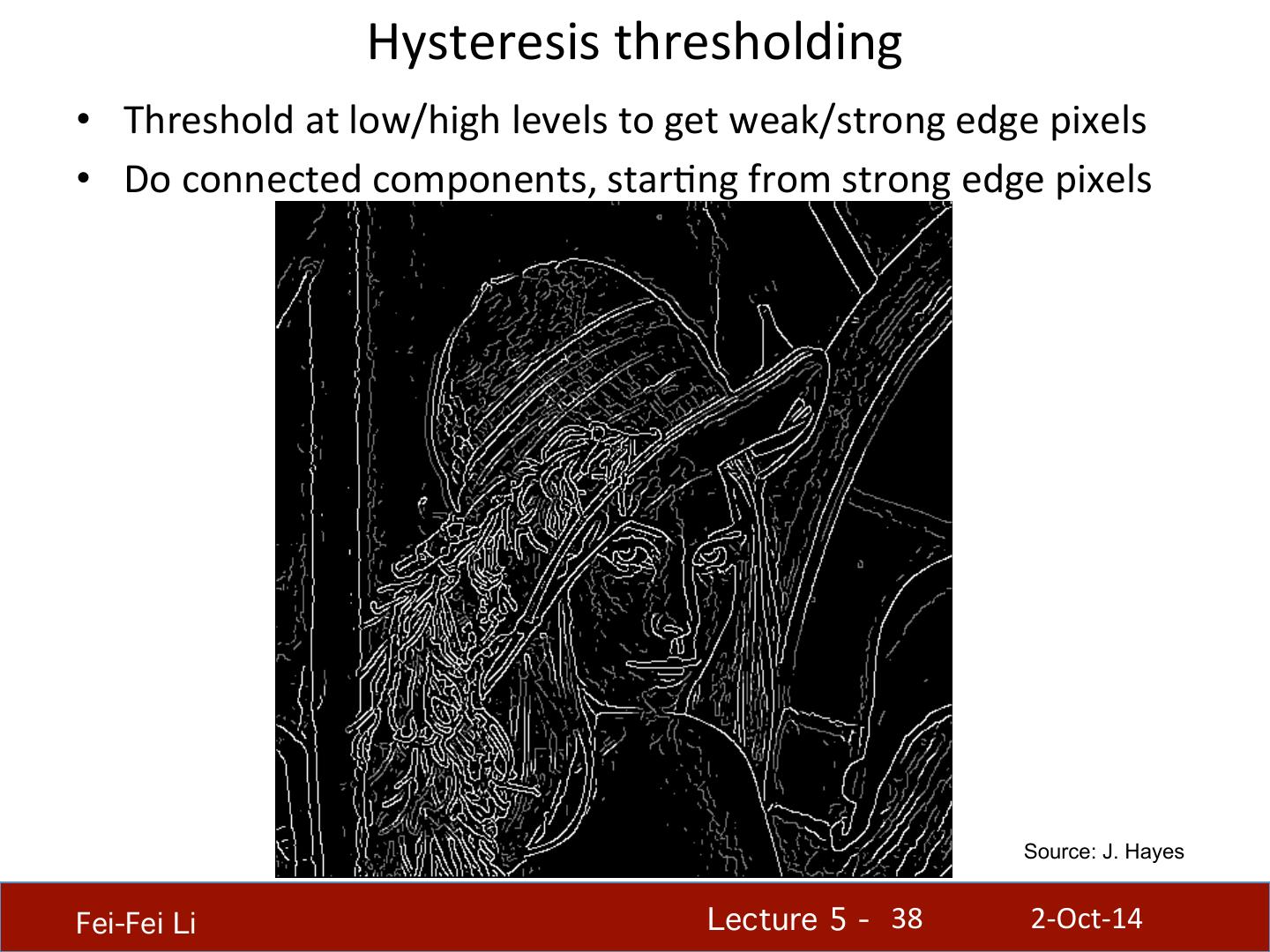
26 . Implementa.on issues • The gradient magnitude is large along a thick “trail” Source: D. Forsyth or “ridge,” so how do we iden.fy the actual edge points? • How do we link the edge points to form curves? Fei-Fei Li! Lecture 5 - !26 2-‐Oct-‐14
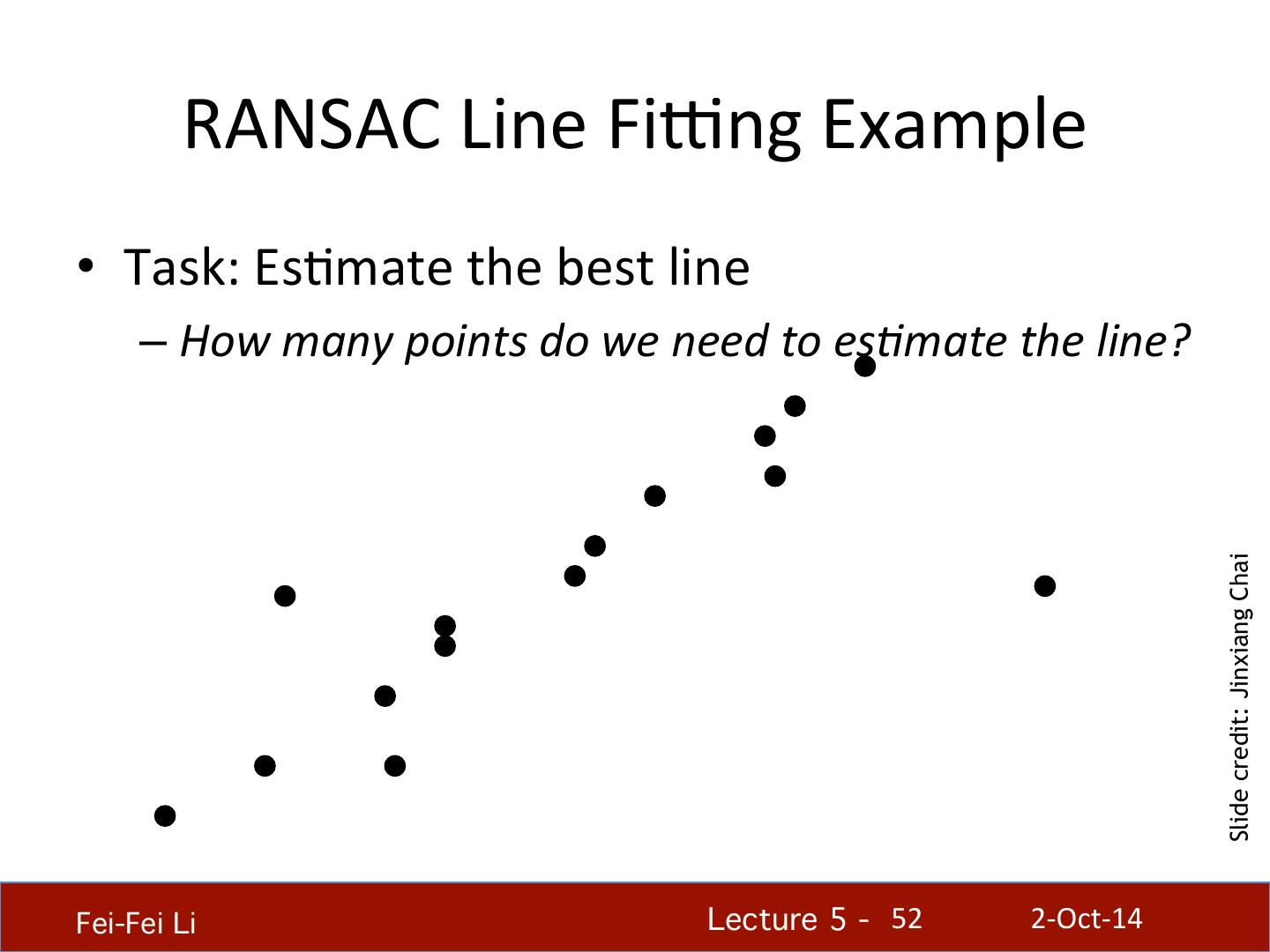
27 . Designing an edge detector • Criteria for an “op.mal” edge detector: – Good detec,on: the op.mal detector must minimize the probability of false posi.ves (detec.ng spurious edges caused by noise), as well as that of false nega.ves (missing real edges) – Good localiza,on: the edges detected must be as close as possible to the true edges – Single response: the detector must return one point only for each true edge point; that is, minimize the number of local maxima around the true edge Fei-Fei Li! Lecture 5 - !27 2-‐Oct-‐14
28 . What we will learn today • Edge detec.on • A simple edge detector • Canny edge detector • A model fiIng method for edge detec.on – RANSAC Fei-Fei Li! Lecture 5 - !28 2-‐Oct-‐14
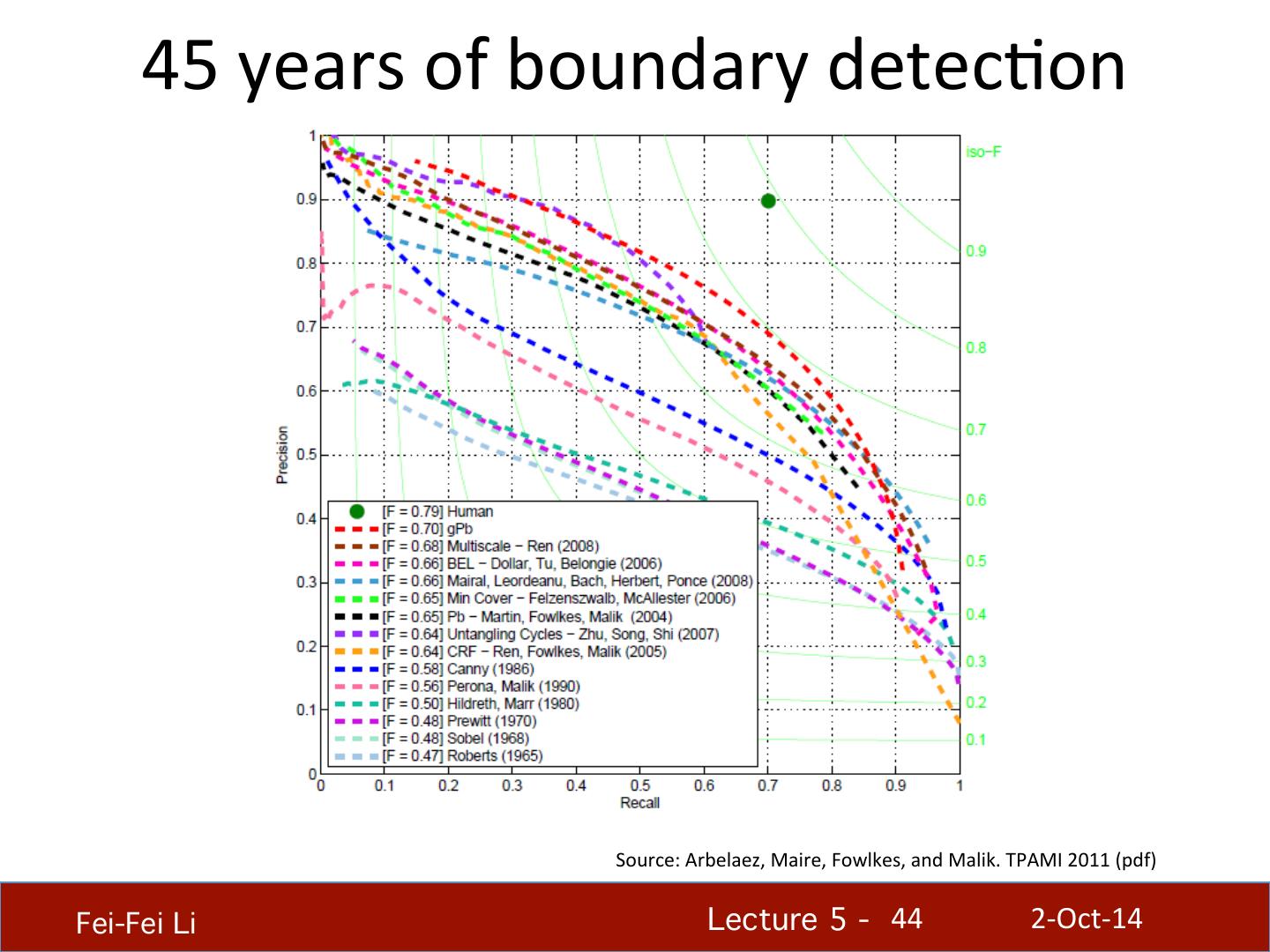
29 . Canny edge detector • This is probably the most widely used edge detector in computer vision • Theore.cal model: step-‐edges corrupted by addi.ve Gaussian noise • Canny has shown that the first deriva.ve of the Gaussian closely approximates the operator that op.mizes the product of signal-‐to-‐noise ra7o and localiza.on J. Canny, A Computa*onal Approach To Edge Detec*on, IEEE Trans. Pamern Analysis and Machine Intelligence, 8:679-‐714, 1986. Fei-Fei Li! Lecture 5 - !29 2-‐Oct-‐14