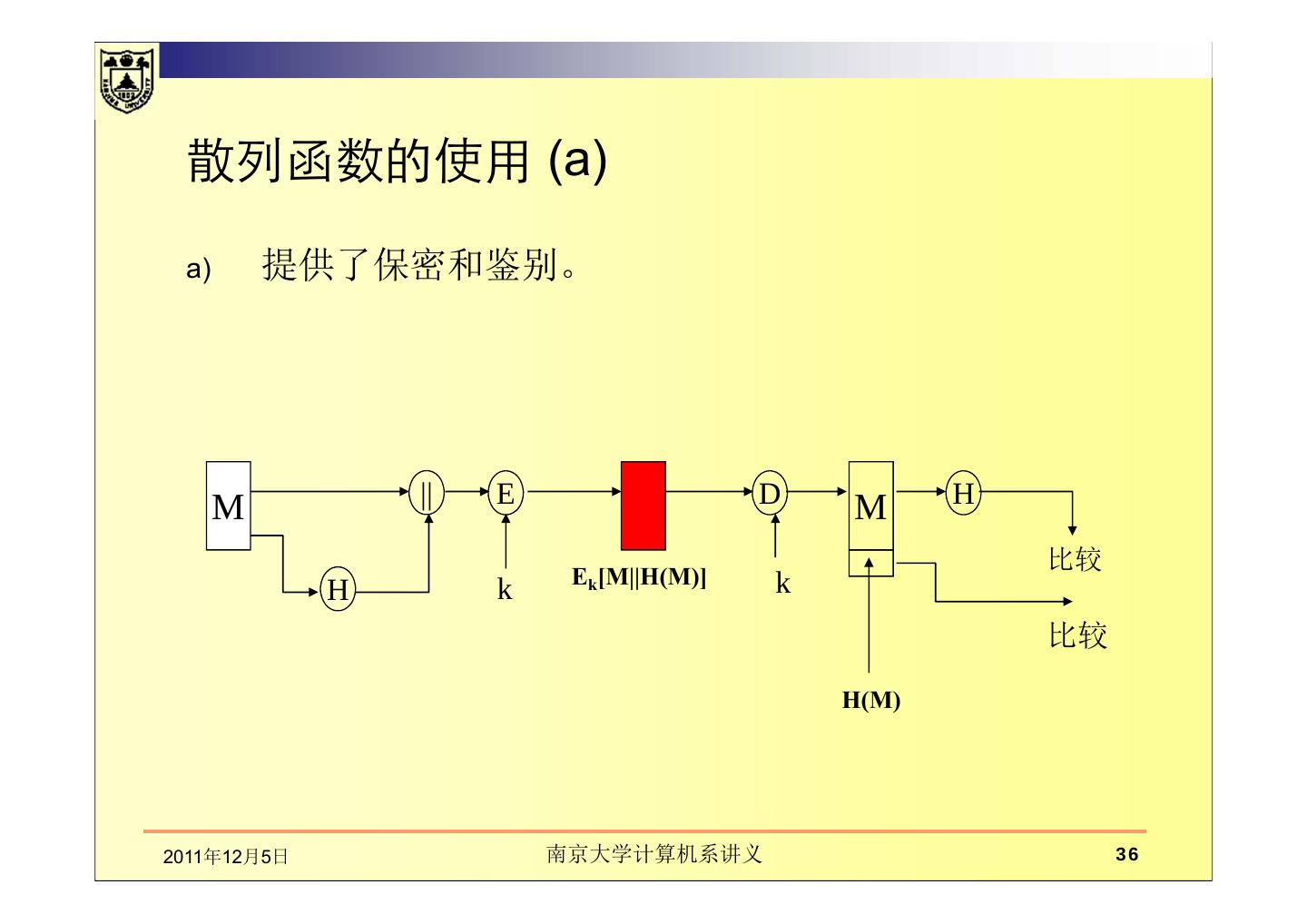
计算机系统信息安全：数据完整性及散列函数

1 .第3章 数据完整性与散列函数 南京大学计算机系黄皓教授 2011年10月19日星期三 

2 . 参考文献 1. Wenbo Mao(毛文波)，现代密码学理论与实践，电子 工业出版社，2004年7月。 2. W. Stallings（杨明等译），编码密码学与网络安全- 原理与实践，电子工业出版社。2001年4月。 2011年12月5日星期一 南京大学计算机系讲义 2 

3 . 内容 1. 数据完整性的基本概念； 2. 散列函数； 3. 密码散列报文鉴别码 2011年12月5日 南京大学计算机系讲义 3 

4 .1. 基本概念 

5 .1. 基本概念 数据完整性需求  我们关于开放通信网络的脆弱性做了一个理想的、标准 的假设： 所有的通信都经受一个称为Malice的攻击者，他可以随意地窃听、 截取、重发、修改、伪造或插入消息。 当Malice插入了修改过的或伪造的消息，他将试图欺骗目标接收 者，使其相信该消息来自某个其他合法的主体。 我们需要一种机制，使得消息的接收者可以验证该消息是否是来 自所声称的消息源，且在传输的过程中是否受到未授权方式修改。 数据完整性就是抗击对消息未授权修改的安全服务。 2011年12月5日 南京大学计算机系讲义 5 

6 .1. 基本概念 差错控制与数据完整性  检错码  检测由于通信的缺陷而导致消息发生错误的方法。  通过这种编码加入的冗余度使得消息的接收者可以采用极大似 然检测器来判定接收到的码字应该译为哪条消息。  数据完整性  消息的发送者通过编码为消息增加一些冗余来生成一个“校验 值”，并将该校验值附在消息之后；  消息的接收者根据与发送者协商好的一系列规则，利用附加的 校验值来检验所接收到的消息的正确性。  使得加入的校验值在整个校验值空间中尽可能地均匀分布，这 就使得攻击者伪造一个有效校验值的概率达到最小。 2011年12月5日 南京大学计算机系讲义 6 

7 .1. 基本概念 篡改检测码  设M是任意的信息，Ke为编码密钥，Kv是验证密钥，  篡改检测码的生成：MDC＝f(Ke, M) (Manipulation Detection Code)  篡改检测码的验证：  true, 概率为 1， 如果 MDC=f(Ke, M) G(Kv, M, MDC) =  false, 压倒性概率， 如果 MDC  f(Ke, M) 信源，附加值 信源变换 信宿验证 信源 Ke Kv 密钥生成 2011年12月5日 南京大学计算机系讲义 7 

8 .1. 基本概念 完整性的保护  完整性保护的应用  数据通信  数据存储  完整性保护的机制  对称技术  密码散列函数  密码函数  非对称技术：数字签名 2011年12月5日 南京大学计算机系讲义 8 

9 . 消息摘要 存储问题：  假定M是要存储的消息。  h是一个Hash函数，y=h(M)称为消息M的摘要。  安全地保存h，  我们希望如果消息M改变成了M’，则h(M) ≠h(M’)。  如果这样，我们可以用消息摘要h(M)来验证消息M是否被改变。 通信问题：  假定M是要发送的消息。  消息M的摘要y随着消息一起发送M||y，接收者验证y是否等于h(M)。  问题：M||h(M) → M’ || h(M’)，h是公开的，攻击者可以完成这 样的篡改，接收者无法发现消息的改变。  带密钥hash：y=h(k, M)。  攻击者无法完成篡改：M||h(k, M) → M’ || h(k, M’) ，因为没有密钥k。 2011年12月5日 南京大学计算机系讲义 9 

10 .1. 基本概念 密码散列函数  由对称密码技术生成的MDC常称为消息认证码(MAC， Message Authentication Code)。  散列函数h是一个确定的函数，它将任意长的比特串映射 为定长|h|比特串的杂凑值。  我们希望h具有以下性质：  混合变换 对于任意的输入x，输出的杂凑值h(x)应当和区间[ 0, 2|h| ]中均匀的二进制串在计算上是不可区分的。  抗碰撞攻击(强冲突) 找两个输入x和y，且x≠y，使得h(x)=h(y)， 在计算上应当是不可行 的。为使这个假设成立，要求h的输出 空间应当足够的大。|h|最小为128，而典型的值为160。 (例 如：合同欺骗)  抗原像攻击 (弱冲突) 已知一个杂凑值h，找一个输入串x，使 得h=h(x)，在计算上是不可行的。 (例如：篡改) 2011年12月5日 南京大学计算机系讲义 10 

11 . RSA签名体制  密钥建立  用户Alice的公钥为(N，e)，(N, p, q, d)为私钥。  其中N=pg，p和g是两个长度差不多的大素数，e是满足gcd( e， φ(N))=1的整数。整数d，满足ed = 1 mod (φ(N) )。  签名生成  消息的m的签名：  S = Signd (m) ← md mod (N)  签名验证  设Bob是验证者，他知道公钥(N，e)属于Alicec，给定一个消息 -签名对(m，s)。  Bob的验证过程为 Verify(N, e)(m, s) = True, 如果m=se (mod N) 2011年12月5日 南京大学计算机系讲义 11 

12 . EIGamal签名体制  生成密钥对  生成一个大的随机素数p和整数mod p的乘法群Zp* 的生成元α;  选取一个随机整数s (1≤ s ≤p-2), 计算β＝ αs (mod p);  公钥(p, α, β), 私钥s。  对信息m签名  选取一个随机整数 k (1≤k≤p-2)，计算X=αk mod p  从方程 m = (s · X + k · Y) mod (p-1) 中求解Y;  签名为(X,Y);  验证签名  验证等式： βX · XY ?= αm mod p  (αs )X· (αk )Y = αs · X + k · Y mod p = αm + t ·(p-1) mod p = αm · α t ·(p-1) mod p = αm mod p 2011年12月5日 南京大学计算机系讲义 12 

13 . 椭圆曲线密码体制 — 签名与验证ECSA 对信息m签名 验证签名(r, s) I. 将m表示成一个二进制串 I. 查找公钥(E(Fq),P,n,Q), II. 计算hash值 e= H(m); II. 计算点 (x1,y1)=sP+rQ III. 在区间[1，n-1]内选取一个随 III. 计算hash值 e= H(m); 机数k, IV. 计算R=(x1+e) mod q; IV. 计算点 (x1,y1):=k·P (k个P相 ） V. 如果R=r，则接受签名。 V. 计算r=(x1+e) mod q; VI. 利用私钥d计算 s=(k-d · r) mod n VII. 签名(r, s) 。 2011年12月5日 南京大学计算机系讲义 13 

14 .2. 散列函数 

15 . 散列函数的目标  散列函数的目的是为文件、报文或其他的分组数据产生 “指纹”。要用于报文鉴别，散列函数H必须具有如下性质： 1. H能用于任何大小的数据分组。 2. H产生定长输出。 3. 对任何给定的x，H(x)要相对易于计算，使得硬件和软件实现成为实 际可行。 4. 对任何给定的码H(x)，从H(x)计算x，在计算上是不可行的。这就是 所谓的单向性质。 5. 对任何给定的分组x，寻找不等于x的y，使得H(y)=H(x)在计算上是 不可行的。 6. 寻找对任何的(x,y)对使得H(x)=H(y)在计算上是不可行的。 2011年12月5日 南京大学计算机系讲义 15 

16 . 合同欺骗的例子  Alice准备一份合同的两个版本，一份对Bob有利，一份将使他破产；  Alice对这两种版本的每一份都作一个细微的改变（例如，在回车之 前加一个或二个空格，通过在n行中作修改，则可以得到2n种不同的 文件）。  Alice比较这两种版本的散列值，找出相匹配的一对(N,M)， 其中对 M对Bob有利,N将使他破产，并且H(M)=H(N)。  Alice请求Bob对合同M签名：M || E(KRBob, H(M) )  Alice 在适当的时候向法官证明Bob签署过合同： N || E(KRBob, H(N) ) ( = N || E(KRBob, H(M) ) ) 2011年12月5日 南京大学计算机系讲义 16 

17 . 构造意义相同的冲突报文 Dear Anthony, This letter is you to Mr. P. to introduce Alfred I am writing to you -- -- new chief Barton, the jewellery buyer for newly appointed senior 2011年12月5日 南京大学计算机系讲义 17 

18 . Alice 要作多少次修改？ 2011年12月5日 南京大学计算机系讲义 18 

19 . 生日攻击  给定x,y, H(x)=H(y)的概率为1/n;  假设一年365天， n=365 n为H的可能的函数值的个数；  k个人中没有人生日相同的概 如果H(x)是m位的整数，则n=2m。 率。 n(n-1)     （n－k+1)  给定H(x1), H(x2),…, H(xk), H(x1) p= 至少与某个H(xi) 相同的概率为 nk [ 1-（1-1/n) k] ≈k/n； ≈1- e –k(k-1)/2n  如果H(x)的可能的函数值个数为  p>1/2 的最小k是多少？ 2m，则H(x1)至少与某个H(xi) k=(2(ln2)n)1/2 (i=2,..,k) 相同的概率大于1/2的最 ≈1.18 n1/2 小的k值为2m/2。 ≈23 ( 如果n=365) 2011年12月5日 南京大学计算机系讲义 19 

20 . 散列函数的强行攻击  单向： 给定h， 求x使得H(x)=h; 2n  弱抗冲突：给定H(x)，求y使得H(y)=H(x); 2n  强抗冲突：求x, y， 使得H(y) = H(x); 2n-1 2011年12月5日 南京大学计算机系讲义 20 

21 . 散列函数的密码分析  着重分析压缩函数f的内部结构，寻找对单次运行后就能 产生冲突的高效技术； 2011年12月5日 南京大学计算机系讲义 21 

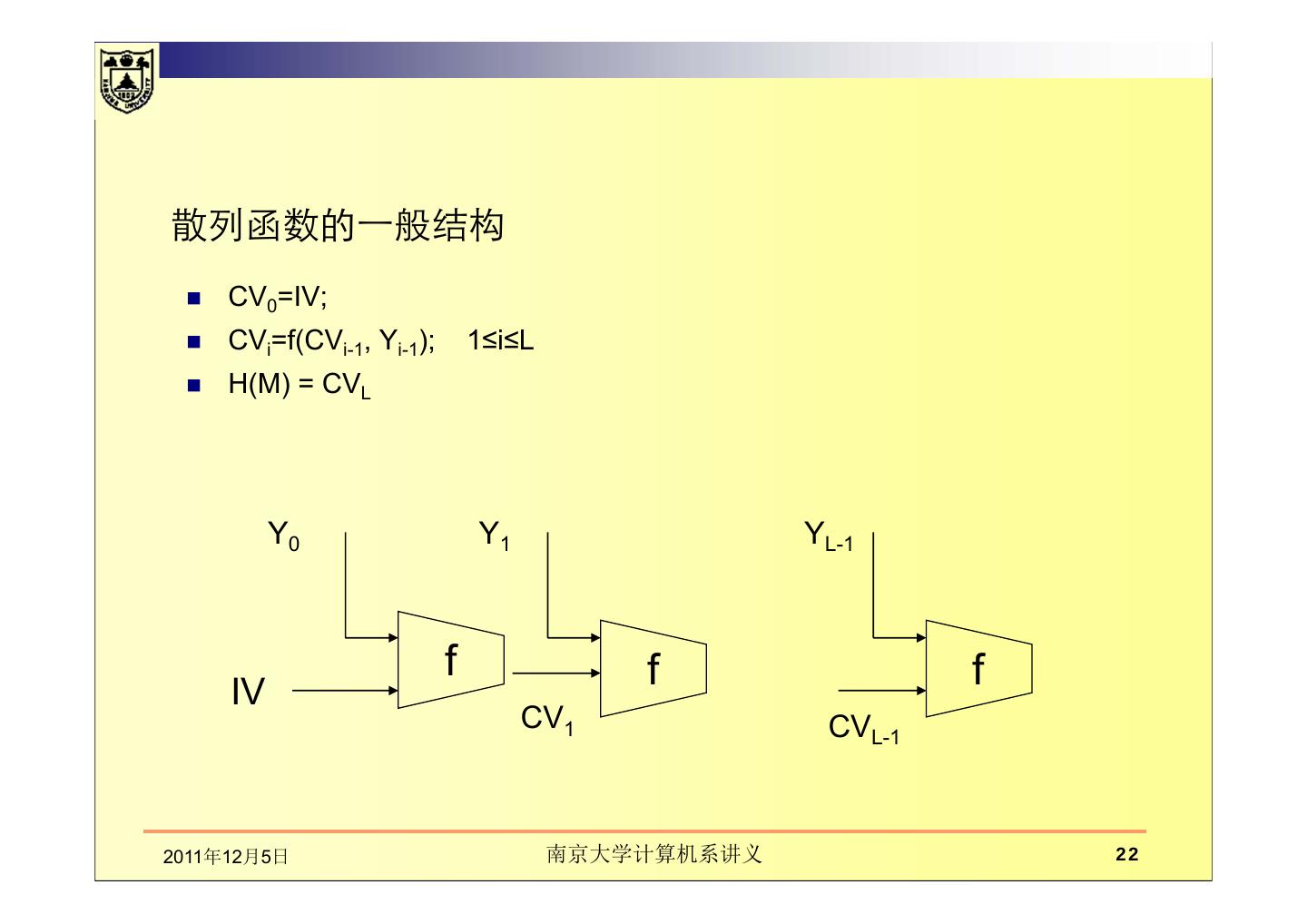
22 .散列函数的一般结构  CV0=IV;  CVi=f(CVi-1, Yi-1); 1≤i≤L  H(M) = CVL Y0 Y1 YL-1 f f f IV CV1 CVL-1 2011年12月5日 南京大学计算机系讲义 22 

23 . 2.2 MD5报文摘要算法 (Rivest， RFC1321) 填充 长度 报文 L*512-64-填充长度 1-512 64 Y0 512 Y1 512 · · · Yq 512 · · · YL-1 512 IV HMD5 HMD5 HMD5 HMD5 CV1 CVq CVL-1 128位摘要 2011年12月5日 南京大学计算机系讲义 23 

24 .  MD5: RFC1321  MD4: RFC1320  MD2: RFC1319 2011年12月5日 南京大学计算机系讲义 24 

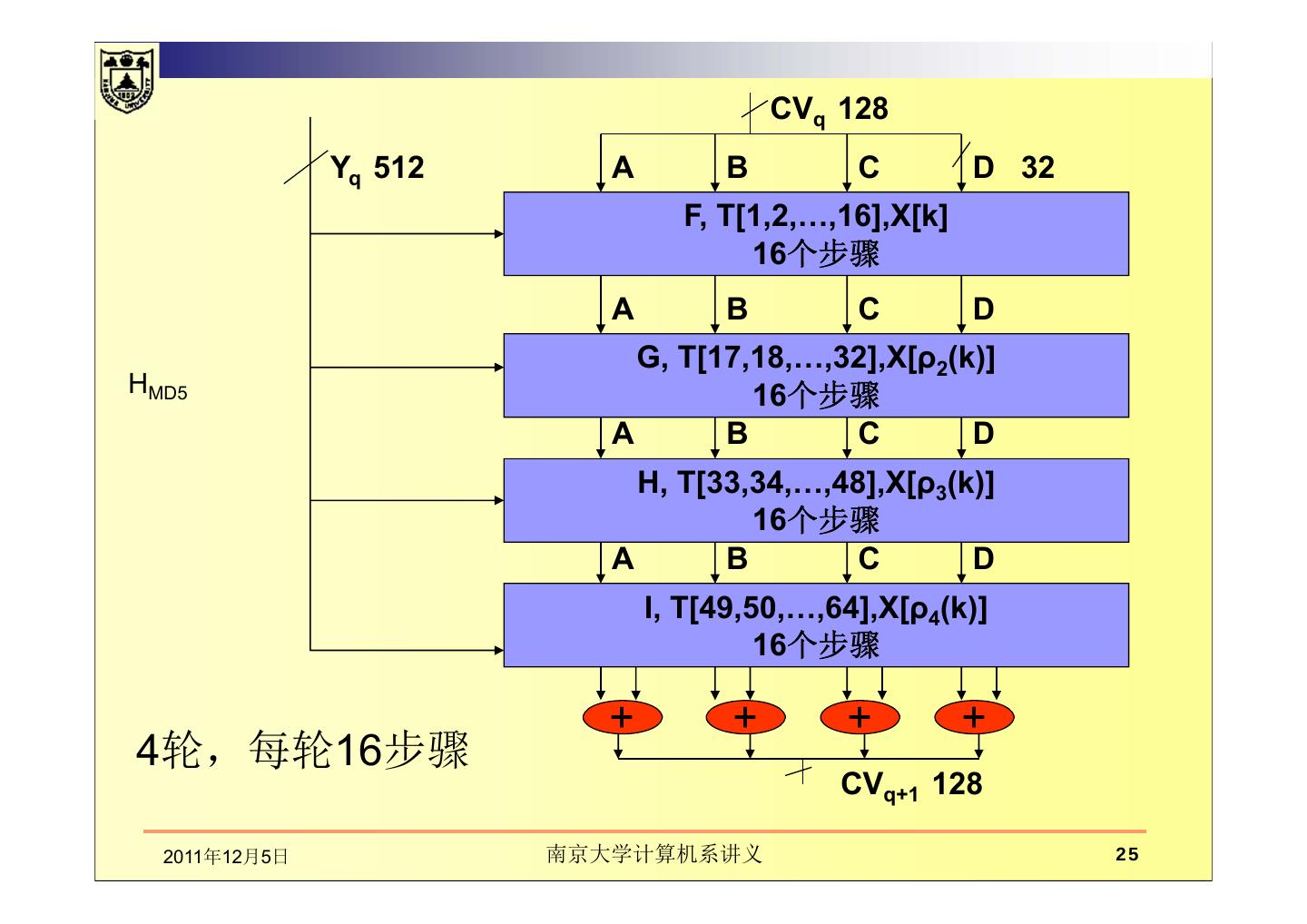
25 . CVq 128 Yq 512 A B C D 32 F, T[1,2,…,16],X[k] 16个步骤 A B C D G, T[17,18,…,32],X[ρ2(k)] HMD5 16个步骤 A B C D H, T[33,34,…,48],X[ρ3(k)] 16个步骤 A B C D I, T[49,50,…,64],X[ρ4(k)] 16个步骤 + + + + 4轮，每轮16步骤 CVq+1 128 2011年12月5日 南京大学计算机系讲义 25 

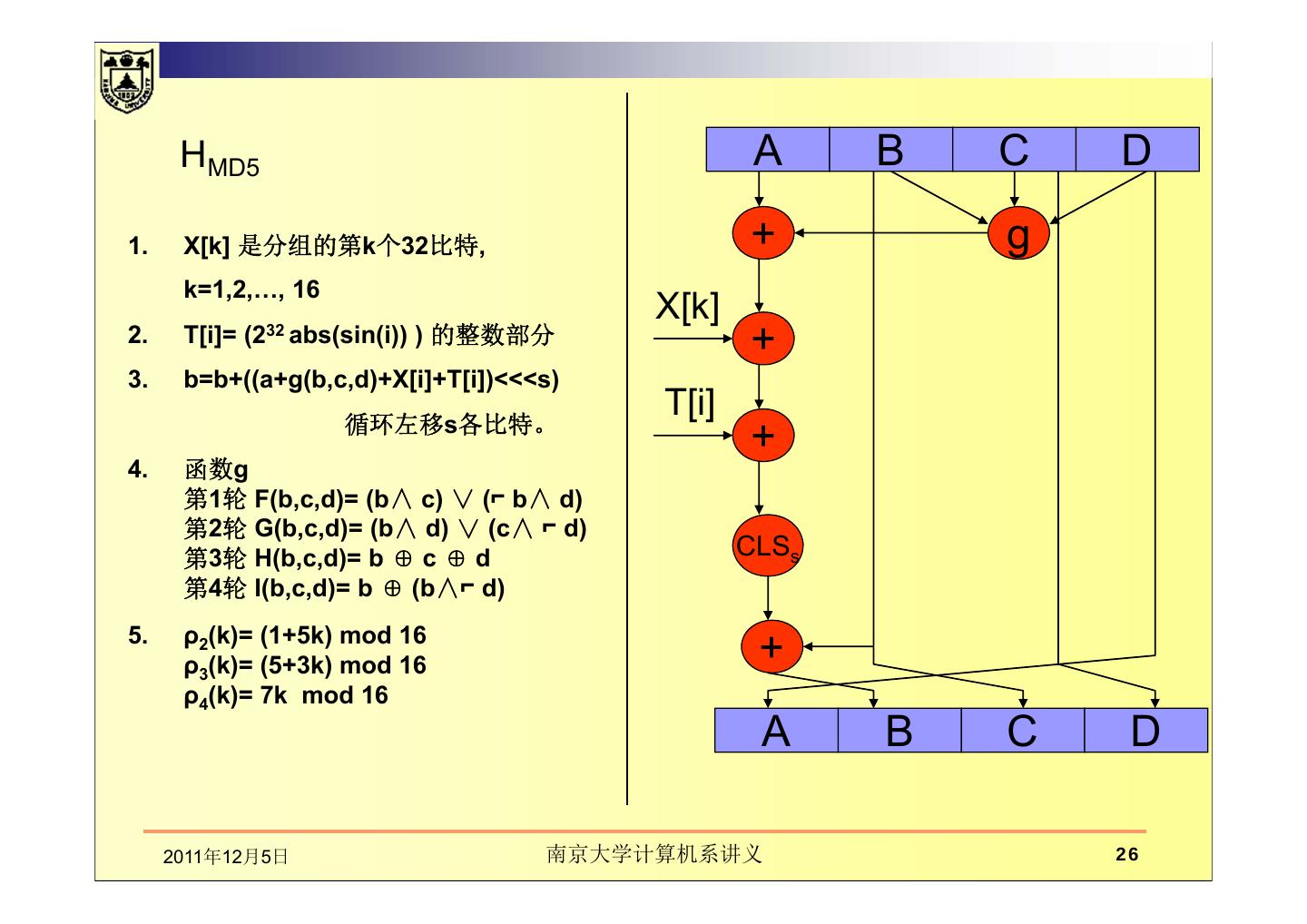
26 . HMD5 A B C D 1. X[k] 是分组的第k个32比特, + g k=1,2,…, 16 X[k] 2. T[i]= (232 abs(sin(i)) ) 的整数部分 + 3. b=b+((a+g(b,c,d)+X[i]+T[i])<<<s) 循环左移s各比特。 T[i] + 4. 函数g 第1轮 F(b,c,d)= (b∧ c) ∨ (⌐ b∧ d) 第2轮 G(b,c,d)= (b∧ d) ∨ (c∧ ⌐ d) 第3轮 H(b,c,d)= b ⊕ c ⊕ d CLSs 第4轮 I(b,c,d)= b ⊕ (b∧⌐ d) 5. ρ2(k)= (1+5k) mod 16 ρ3(k)= (5+3k) mod 16 + ρ4(k)= 7k mod 16 A B C D 2011年12月5日 南京大学计算机系讲义 26 

27 . MD5的强度  Rivest猜想MD5  给定H(x)，求y使得H(y)=H(x)需要2128数量级的操作  求x,y，使得H(y)=H(x)的操作，需要264数量级的操作  1996年Dobbertin 提出了针对MD5单轮压缩函数的攻击。  2004年8月17日在美国加州圣巴巴拉国际密码学会议(Crypto’2004) 上，山东大学王小云教授等报告了MD5的破解方法。 2011年12月5日 南京大学计算机系讲义 27 

28 . 2.3 SHA-1  安全散列算法(SHA)由美国国家标准和技术协会(NIST) 提出，作为联邦信息处理标准(FIPS PUB 180) 在1993 年公布。  1995年发布了一个修订版 FIPS PUB 180-1通常称为 SHA-1  SHA也是基于MD4的。  最大报文长度264-1，散列码长度160bit。  结构与MD5类似，抗攻击能力比MD5强； 2011年12月5日 南京大学计算机系讲义 28 

29 .2.4 RIPEMD-160  欧共体的RIPE项目研制的；  MD4的变种，为抵抗已知的关于MD4、MD5的攻击而设 计的；  摘要长度为160，报文长度不受限制; 2011年12月5日 南京大学计算机系讲义 29