LEO - DB2's LEarning Optimizer

1 . LEO – DB2’s LEarning Optimizer Michael Stillger3*, Guy Lohman1, Volker Markl1, Mokhtar Kandil2 1 2 3* IBM Almaden Research Center IBM Canada Ltd. Siebel Systems, Inc. 650 Harry Road, K55/B1 1150 Eglinton Ave. E. 2207 Bridgepointe Parkway San Jose, CA, 95139 Toronto, ON M3C 1H7 San Mateo, CA 94404 USA Canada USA mstilger@siebel.com, {lohman, marklv}@almaden.ibm.com, mkandil@ca.ibm.com Abstract 1. Introduction Most modern DBMS optimizers rely upon a cost model to choose the best query execution plan (QEP) for any Most modern query optimizers for relational database given query. Cost estimates are heavily dependent management systems (DBMSs) determine the best query upon the optimizer’s estimates for the number of rows execution plan (QEP) for executing an SQL query by that will result at each step of the QEP for complex mathematically modeling the execution cost for each plan queries involving many predicates and/or operations. and choosing the cheapest QEP. This execution cost is These estimates rely upon statistics on the database and largely dependent upon the number of rows that will be modeling assumptions that may or may not be true for a processed by each operator in the QEP. Estimating the given database. In this paper we introduce LEO, DB2's number of rows – or cardinality – after one or more LEarning Optimizer, as a comprehensive way to repair predicates have been applied has been the subject of much incorrect statistics and cardinality estimates of a query research for over 20 years [SAC+79, Gel93, SS94, execution plan. By monitoring previously executed ARM89, Lyn88]. Typically this estimate relies on queries, LEO compares the optimizer’s estimates with statistics of database characteristics, beginning with the actuals at each step in a QEP, and computes number of rows for each table, multiplied by a filter factor adjustments to cost estimates and statistics that may be – or selectivity – for each predicate, derived from the used during future query optimizations. This analysis number of distinct values and other statistics on columns. can be done either on-line or off-line on a separate The selectivity of a predicate P effectively represents the system, and either incrementally or in batches. In this probability that any row in the database will satisfy P. way, LEO introduces a feedback loop to query While query optimizers do a remarkably good job of optimization that enhances the available information on estimating both the cost and the cardinality of most the database where the most queries have occurred, queries, many assumptions underlie this mathematical allowing the optimizer to actually learn from its past model. Examples of these assumptions include: mistakes. Our technique is general and can be applied Currency of information: The statistics are assumed to any operation in a QEP, including joins, derived to reflect the current state of the database, i.e. that the results after several predicates have been applied, and database characteristics are relatively stable. even to DISTINCT and GROUP-BY operators. As Uniformity: Although histograms deal with skew in shown by performance measurements on a 10 GB TPC- values for “local” selection predicates (to a single table), H data set, the runtime overhead of LEO’s monitoring we are unaware of any available product that exploits is insignificant, whereas the potential benefit to them for joins. response time from more accurate cardinality and cost Independence of predicates: Selectivities for each estimates can be orders of magnitude. predicate are calculated individually and multiplied together, even though the underlying columns may be related, e.g. by a functional dependency. While multi- Permission to copy without fee all or part of this material is granted dimensional histograms address this problem for local provided that the copies are not made or distributed for direct predicates, again they have never been applied to join commercial advantage, the VLDB copyright notice and the title of the publication and its date appear, and notice is given that copying is by predicates, aggregation, etc. Applications common today permission of the Very Large Data Base Endowment. To copy have hundreds of columns in each table and thousands of otherwise, or to republish, requires a fee and/or special permission from tables, making it impossible to know on which subset(s) the Endowment of columns to maintain multi-dimensional histograms. Proceedings of the 27th VLDB Conference, Roma, Italy, 2001 * Work performed while the author was a post-doc at IBM ARC. 

2 . Principle of inclusion: The selectivity for a join predicates against those tables. Recent work has extended predicate X.a = Y.b is typically defined to be 1/max{|a|, one-dimensional equi-depth histograms to more |b|}, where |b| denotes the number of distinct values of sophisticated and accurate versions [PIHS96] and to column b. This implicitly assumes the “principle of multiple dimensions [PI97]. This classical work on inclusion”, i.e. that each value of the smaller domain has a histograms concentrated on the accuracy of histograms in match in the larger domain (which is frequently true for the presence of skewed data and correlations by scanning joins between foreign keys and primary keys). the base tables completely, at the price of high run-time When these assumptions are invalid, significant errors cost. The work in [GMP97] deals with the necessity of in the cardinality – and hence cost -- estimates result, keeping histograms up-to-date at very low cost. Instead of causing sub-optimal plans to be chosen. From the computing a histogram on the base table, it is authors’ experience, the primary cause of major modeling incrementally derived and updated from a backing sample errors is the cardinality estimate on which costs depend. of the table, which is always kept up-to-date. Updates of Cost estimates might be off by 10 or 15 percent, at most, the base table are propagated to the sample and can for a given cardinality, but cardinality estimates can be off trigger a partial re-computation of the histogram, but there by orders of magnitude when their underlying is no attempt to validate the estimates from these assumptions are invalid. Although there has been histograms against run-time actuals. considerable success in using histograms to detect and The work of [CR94] and [AC99] are the first to correct for data skew [IC91, PIHS96, PI97], and in using monitor cardinalities in query executions and exploit this sampling to gather up-to-date statistics [HS93, UFA98], information in future compilations. In [CR94] the result there has to date been no comprehensive approach to cardinalities of simple predicates after the execution of a correcting all modeling errors, regardless of origin. query are used to adapt the coefficients of a curve-fitting This paper introduces LEO, the LEarning Optimizer, formula. The formula approximates the value distribution which incorporates an effective and comprehensive of a column instead of employing histograms for technique for a query optimizer actually to learn from any selectivity estimates. In [AC99] the authors present a modeling mistake at any point in a QEP, by automatically query feedback loop, in which actual cardinalities gleaned validating its estimates against actuals for a query after it from executing a query are used to correct histograms. finishes executing, determining at what point in the plan Multiple predicates can be used to detect correlation and the significant errors occurred, and adjusting its model update multi-dimensional histograms. This approach dynamically to better optimize future queries. Over time, effectively deals with single-table predicates applied LEO amasses experiential information that augments and while accessing a base table, but the paper does not deal adjusts the database statistics for the part of the database with join predicates, aggregation, and other operators, nor that enjoys the most user activity. Not only does this does it specify how the user is supposed to know on information enhance the quality of the optimizer’s which columns multi-dimensional histograms should be estimates, but it also can suggest where statistics created. LEO’s approach extends and generalizes this gathering should be concentrated or even can supplant the pioneering work. It can learn from any modeling error at need for statistics collection. LEO has been prototyped any point in a QEP, including errors due to local on IBM’s DB2 Universal Data Base (UDB) on the predicates, expressions of base columns involving user- Windows, Unix, and OS/2 platforms (hereafter referred to defined functions, predicates involving parameter markers simply as “DB2”), and has proven to be very effective at or host variables, join predicates, keys created by the correcting cardinality estimation errors. DISTINCT or GROUP BY clauses, derived tables, and This paper is organized as follows. Section 2 explores any correlation between any of the above. Most of these the previous literature in relation to LEO. We give an operations that change cardinality in some way cannot be overview of LEO and an example of its execution in addressed by histograms. LEO can even adjust estimates Section 3. Section 4 details how LEO works, including of other parameters such as buffer utilization, sort heap the four major components of capturing the optimizer’s consumption, I/Os, or the actual running time -- the only plan, monitoring the execution, analyzing the actuals vs. real limitation to LEO’s approach is the overhead of estimates, and exploiting what is learned in the optimizer collecting the actuals for those estimates. for subsequent queries. In Section 5, we evaluate LEO’s Another research direction focuses on dynamically performance – both its overhead and benefit. Section 6 adjusting a QEP after the execution has begun, by discusses advanced topics and Section 7 contains our monitoring data statistics during the execution (dynamic conclusions and future work. optimization). In [KDeW98] the authors introduce a new statistic collector operator that is compiled into the plan. 2. Related Work The operator collects the row stream cardinality and size and decides whether to continue or to stop the execution Much of the prior literature on cardinality estimates has and re-optimize the remainder of the plan. Query utilized histograms to summarize the data distribution of scrambling in [UFA98] is geared towards the problem of columns in stored tables, for estimating the selectivity of distributed query execution in wide area networks with 

3 .uncertain data delivery. Here the time-out of a data- generation and optimization, code generation, and code shipping site is detected and the remaining data- execution. The gray shaded boxes show the changes made independent parts of the plan are re-scheduled until the to regular query processing to enable LEO’s feedback problem is solved. Both solutions deal with dynamic re- loop: for any query, the code generator dumps essential optimization of (parts of) a single query, but they do not information about the chosen QEP (a plan “skeleton”) save and exploit this knowledge for the next query into a special file that is later used by the LEO analysis optimization run. LEO is aimed primarily at using daemon. In the same way, the runtime system provides information gleaned from one or more query executions monitored information about cardinalities for each to discern trends that will benefit the optimization of operator in the QEP. Analyzing the plan skeletons and the future queries. This benefit is not limited to just the same runtime monitoring information, the LEO analysis query, because the exact same query is seldom re- daemon computes adjustments that are stored in the executed in modern data warehouses, data marts, and system catalog. The exploitation component closes the business intelligence applications. Any query with feedback loop by using the adjustments in the system predicates or aggregation on the same column(s) can catalog to provide adjustments to the query optimizer’s exploit LEO’s learning. LEO does not (yet) address the cardinality estimates. issue of changing in mid-stream the QEP of a running query, as did [KDeW98] and [UFA98], although it could. 64/ 4XHU\ SQL Compiler Doing this correctly in a real product needs to resolve Optimizer many hard issues not addressed by that work, such as 1. Preparation Phase compute filter factors determining points where such changes produce correct LEO Feedback results (i.e., where data is fully materialized, before any Exploitation 2. Planning Phase results are returned to the user), and reliably predicting Opt. estimate cardinalities 6\VWHP &DWDORJ the times to re-optimize and execute a new plan so that Plan Code Generator Adjustments they can be traded off against the time to complete the LEO /(2 Skeleton original plan. 6HFWLRQV QEP Skeleton File $QDO\VLV 'DHPRQ 1. analyze plan skeletons Runtime System and monitor file 3. A Learning Optimizer LEO Execution Monitor File 2. compute adjustments 3. update/append Monitor system catalog This section gives an overview of LEO’s design, a 4XHU\ 5HVXOW simplified example of how it learns, and some of the practical issues that it must deal with. Figure 1: LEO Architecture 3.1 An Overview of LEO 3.2 Monitoring and Learning: An Example LEO exploits empirical results from actual executions of In the following we use as an example the SQL query: queries to validate the optimizer’s model incrementally, SELECT * FROM X, Y, Z deduce what part of the optimizer’s model is in error, and WHERE X.Price >= 100 AND Z.City = ‘Denver’ compute adjustments to the optimizer’s model. AND Y.Month = ‘Dec’ AND X.ID = Y.ID LEO is comprised of four components: a component AND Y.NR = Z.NR to save the optimizer’s plan, a monitoring component, an GROUP BY A analysis component, and a feedback exploitation Figure 2 shows the skeleton of a QEP for this statement, component. The analysis component is a standalone including the statistical information and the optimizer’s process that may be run separately from the DB2 server, cardinality estimates. In addition, the figure also shows and even on another system. The remaining three the actual cardinalities that the monitoring component of components are modifications to the DB2 server: plans LEO determined during query execution. are captured at compile time by an addition to the code In the Figure, cylinders indicate base table access generator, monitoring is part of the run-time system, and operators such as index scan (IXSCAN) or table scan feedback exploitation is integrated into the optimizer. (TBSCAN), ellipses indicate other operators, such as The four components can operate independently, but nested loop joins (NLJOIN) and grouping (GROUP BY). form a consecutive sequence that constitutes a continuous “Stat” denotes the base table cardinality, as stored in the learning mechanism by incrementally capturing plans, system catalog, and “Est:” denotes the optimizer’s monitoring their execution, analyzing the monitor output, estimate for the result cardinality of each table access and computing adjustments to be used for future query operator. after application of any predicates (e.g., X.Price compilations. >= 100), as well as for each of the nested-loop join operators. During query execution, the LEO monitoring Figure 1 shows how LEO is integrated into the component measures the comparable actual cardinality architecture of DB2. The left part of the figure shows the (“Act”) for each operator. usual query processing flow with query compilation, QEP 

4 . Est: 10 Act: 117 appropriately. This two-layered approach has several advantages. First, we have the option of disabling GROUP BY learning, by simply ignoring the adjustments. This may be Est: 513 Act: 1007 needed for debugging purposes or as a fallback strategy in case the system generated wrong adjustments or the new NL-JOIN optimal plan shows undesired side effects. Second, we can store the specific adjustment value with any plan that Est: 1120 Act: 2112 Est: 149 Act: 133 uses it, so that we know by how much selectivities have NL-JOIN Z.City = "Denver“ already been adjusted and avoid incorrect re-adjustments Est: 1149 Est: 290 IXSCAN Z (no “deltas of deltas”). Lastly, since we keep the Act: 2283 Act: 500 Stat: 23410 Act: 23599 adjustments as catalog tables, we introduce an easily X.Price > 100 Y.Month = “Dec” accessible mechanism for tuning the selectivities of query TBSCAN X ,;6&$1 < Stat: 2100 predicates that could be updated manually by experienced Stat: 7200 Act: 7623 Act: 5949 users, if necessary. Figure 2: Optimal QEP (Skeleton) Consistency between Statistics Comparing actual and estimated cardinalities enables DB2 collects statistics for base tables, columns, indexes, LEO to give feedback to the statistics that were used for functions, and tablespaces, many of which are mutually obtaining the base table cardinalities, as well as to the interdependent. DB2 allows for incremental generation of cardinality model that was used for computing the statistics and checks inconsistencies for user-updateable estimates. This feedback may be a positive reinforcement, statistics. LEO also must ensure the consistency of these e.g., for the table statistics of Z, where the table access interdependent statistics. For example, the number of operator returned an actual cardinality for Z that is very rows of a table determines the number of disk pages used close to that stored in the system catalog statistics. The for storing these rows. When adjusting the number of same holds for the output cardinalities of each operator, rows of a table, LEO consequently also has to ensure such as a positive feedback for the estimate of the consistency with the number of pages of that table -- e.g., restriction on Z that also very closely matches the actual by adjusting this figure as well -- or else plan choices will number. However, it may also be a negative feedback – as be biased. Similarly, the consistency between index and for the table access operator of Y, where the statistics table statistics has to be preserved: If the cardinality of a suggest a number almost three times lower than the actual column that is (a prefix of) an index key is adjusted in the cardinality – or for the join estimates of the nested-loop table statistics, this may also affect the corresponding join between X and Y. In addition, correlations can be index statistics. detected, if the estimates for the individual predicates are known to be accurate but some combination of them is Currency vs. Accuracy not. In all of the above, “predicates” can actually be Creating statistics is a costly process, since it requires generalized to any operation that changes the cardinality scanning an entire table or even the entire database. For of the result. For example, the creation of keys by a this reason, database statistics are often not existent or not DISTINCT or GROUP BY clause reduces the number of accurate enough to help the optimizer to pick the best rows. LEO uses this feedback to help the optimizer to access plan. If statistics are expected to be outdated due to learn to better estimate cardinalities the next time a query later changes of the database or if no statistics are present, involving these tables, predicates, joins, or other operators DB2 fabricates statistics from the base parameters of the is issued against the database. table (file size from the operating system and individual column sizes). The presence of adjustments and fabricated 3.3 Practical Considerations statistics creates a decision problem for the optimizer -- it In the process of implementing LEO, several practical must decide whether to believe possibly outdated considerations became evident that prior work had not adjustments and statistics, or fuzzy but current fabricated addressed. We now discuss some of these general statistics. considerations, and how they affected LEO’s design. When statistics are updated, many of the adjustments calculated by LEO no longer remain valid. Since the set Modifying Statistics vs. Adjusting Selectivities of adjustments that LEO maintains is not just a subset of A key design decision is that LEO never updates the the statistics provided by RUNSTATS, removing all original catalog statistics. Instead, it constructs a second adjustments during an update of the statistics might result set of statistics that will be used to adjust (i.e. repair) the in a loss of information. Therefore any update of the first, original layer. The adjustments are stored as special statistics should re-adjust the adjustments appropriately, tables in the system catalog. The compilation of new in order to not loose information like actual join queries reads these adjustments, as well as the base selectivities and retain consistency with the new statistics. statistics, and adjusts the optimizer’s estimates 

5 .LEO vs. Database Statistics incremented each time an operator processes a row, and LEO is not a replacement for statistics, but a rather a saved after the query completes. LEO can be most complement: LEO gives the most improvement to the effective if this monitoring is on all the time, analyzing modeling of queries that are either repetitive or are similar the execution of every query in the workload. For this to to earlier queries, i.e., queries for which the optimizer’s be practical, LEO’s monitoring component must impose model exploits the same statistical information. LEO minimal overhead on regular query execution extends the capabilities of the RUNSTATS utility by performance. The overhead for incrementing these gathering information on derived tables (e.g., the result of counters has been measured and shown to be minimal, as several joins) and gathering more detailed information discussed in Section 5.1. than RUNSTATS might. Over time, the optimizer’s 4.3 Analyzing Actuals and Estimates estimates will improve most in regions of the database that are queried most (as compared to statistics, which are The analysis component of LEO may be run off-line as a collected uniformly across the database, to be ready for batch process, perhaps even on a completely separate any possible query). However, for correctly costing system, or on-line and incrementally as queries complete previously unanticipated queries, the statistics collected execution. The latter provides more responsive feedback by RUNSTATS are necessary even in the presence of to the optimizer, but is harder to engineer correctly. To LEO. have minimal impact on query execution performance, the analysis component is designed to be run as a low-priority background process that opportunistically seizes “spare 4. The LEO Feedback Loop cycles” to perform its work “post mortem”. Any The following sections describe the details of how LEO mechanism can be used to trigger or continue its performs the four steps of capturing the plan for a query execution, preferably an automated scheduler that and its cardinality estimates, monitoring queries during supervises the workload of the system. Since this means execution, analyzing the estimates versus the actuals, and LEO can be interrupted by the scheduler at any point in the exploitation of the adjustments in the optimization of time, it is designed to analyze and to produce feedback subsequent queries. data on a per-query basis. It is not necessary to accumulate the monitored data of a large set of queries to 4.1 Retaining the Plan and its Estimates produce feedback results. During query compilation in DB2, a code generator To compare the actuals collected by monitoring with component derives an executable program from the the optimizer’s estimates for that query, the analysis optimal QEP. This program, called a section, can be component of LEO must first find the corresponding plan executed immediately (dynamic SQL) or stored in the skeleton for that query. Each plan skeleton is hashed into database for later, repetitive execution of the same query memory. Then for each entry in the monitor dump file (static SQL). The optimal QEP is not retained with the (representing a query execution), it finds the matching section; only the section is available at run-time. The skeleton by probing into the skeletons hash table. Once a section contains one or more threads, which are match is located, LEO needs to map the monitor counters sequences of operators that are interpreted at run-time. for each section operator back to the appropriate QEP Some of the section’s operators, such as a table access, operator in the skeleton. This is not as straightforward as closely resemble similar operators in the QEP. Others, it sounds, because there is not a one-to-one relationship such as those performing predicate evaluation, are much between the section’s operators and the QEP’s operators. more detailed. Though in principle it is possible to In addition, certain performance-oriented optimizations “reverse engineer” a section to obtain the QEP from will bypass operators in the section if possible, thus also which it was derived, in practice that is quite complicated. bypassing incrementing their counters. LEO must detect To facilitate the interpretation of the monitor output for and compensate for this. LEO, we chose to save at compile-time a “skeleton” analyze_main(skeleton root) { subset of the optimal QEP for each query, as an analysis preprocess (root); error = OK; “road map”. This plan skeleton is a subset of the much // construct global state and // pushdown node properties more complete QEP information that may optionally be for (i = 0; i < children(root); i++) obtained by a user through an EXPLAIN of the query, and // for each child contains only the basic information needed by LEO’s {error |= analyze_main(root->child[i]); } // analyze analysis, including the cumulative cardinality estimates if (error) return error; for each QEP operator, as shown in Figure 2. // if error in any child: return error switch (root->opcode) // analyze operator 4.2 Monitoring Query Execution case IXSCAN: return analyze_ixscan(root) case TBSCAN: return analyze_tbscan(root) LEO captures the actual number of rows processed by case … each operator in the section by carefully instrumenting the section with run-time counters. These counters are Figure 3: LEO algorithm 

6 . The analysis of the skeleton tree is a recursive post- the adjustment factors for the table cardinality and the order traversal (see Figure 3). Before actually descending predicate. The cardinality adjustment factor is 7632/7200 down the tree, a preprocessing of the node and its = 1.06. The estimated selectivity of the predicate was immediate children is necessary to construct global state 1149/7200 = 0.1595 while the actual selectivity is information and to push down node properties. The 2283/7632 = 0.2994. The adjustment factor for the skeleton is analyzed bottom up, where the analysis of a corresponding Price < 100 -predicate is (1 - 0.2994) * 1.0 branch stops after an error occurred in the child. Upon / (1 -0.1595) = 0.8335. The optimizer will compute the returning from all children, the analysis function of the selectivity for this predicate in the future to be 1 – 0.8335 particular operator is called. * (1 – 0.1595) = 0.2994. The adjusted table cardinality of the TBSCAN (1.06*7200) times the adjusted predicate Calculating the Adjustments selectivity 0.2994 computes the correct, new estimate of Each operator type (TBSCAN, IXSCAN, FETCH, FILTER, the output cardinality of the TBSCAN operator (2283). GROUP BY, NLJOIN, HSJOIN, etc.) can carry multiple However, different types of section operators can be predicates of different kinds (start/stop keys, pushed used to execute a particular predicate such as ‘Price >= down, join). According to the processing order of the 100’. If the Price column is in the index key, the table predicates within the operator, LEO will find the actual access method could be an IXSCAN-FETCH monitor data (input and output cardinalities of the data combination. If Price is the leading column of the index stream for the predicate) and analyze the predicate. By key, the predicate can be executed as a start/stop key in comparing the actual selectivity of the predicate with the the IXSCAN operator. Then IXSCAN delivers only those estimated selectivity that was stored with the skeleton, rows (with its row identifier or RID) that fulfill the key LEO deduces an adjustment factor such that the DB2 predicate. FETCH uses each RID to retrieve the row from optimizer can later compute the correct selectivity factor the base table. If the predicate on Price cannot be applied from the old estimate and the new adjustment factor. This as a start/stop key, it is executed as a push-down predicate adjustment factor is immediately stored in the database in on every row returned from the start/stop key search. new LEO tables. Note that LEO does not need to re-scan When using a start/stop key predicate, we scan neither the the DB2 catalog tables to get the original statistics, index nor the base table completely, and hence cannot because the estimates that are based on these statistics are determine the actual base table cardinality. In order to stored with the skeleton. determine the real selectivity of an index start/stop key LEO computes an adjustment such that the product of predicate, we can only approximate the needed input the adjustment factor and the estimated selectivity derived cardinality by using the old cardinality estimates, if a from the DB2 statistics yields the correct selectivity. To previously computed table adjustment factor was used1 achieve that, LEO uses the following variables that were The merge-join algorithm demonstrates a similar saved in the skeleton or monitor result: problem that we have named implicit early out. Recall old_est: the estimated selectivity from the optimizer that both inputs of the merge join are sorted data streams. old_adj: an old adjustment factor that was possibly Each row will be matched with the other side until a used to compute old_est higher-valued row or no row at all is found. Reaching the act: The actual selectivity that is computed from the end of the data stream on one side immediately stops the monitor data algorithm. Thus any remaining rows from the other side After detecting an error ( | old_est – act | / act > 0.05 ) will never be asked for, and hence are not seen or counted for the predicate col < X, LEO computes the adjustment by the monitor. As a result, any monitor number for factor so that the new estimate equals the actual value merge-join input streams is unreliable unless we have (act) computed from the monitor: est = actual = stats*adj; encountered a “dam” operator such as SORT or TEMP, where stats is the original selectivity as derived from the which by materializing all rows ensures the complete scan catalog. The old estimate (old_est) is either equivalent to and count of the data stream prior to the merge join. the original statistic estimate (stats) or was computed with an old adjustment factor (old_adj). Hence this old Storing the Adjustments adjustment factor needs to be factored out. (adj = act / For storing the adjustments, the new tables stats = act/(old_est/old_adj) = act*(old_adj/old_est). LEO_TABLES, LEO_COLUMNS and LEO_JOINS have Since the selectivity for the predicate (col >= X) is 1 – been introduced into the DB2 system catalog. selectivity(col < X), we invert the computation of the Take as an example the column adjustment catalog as estimate and the adjustment factor for this type of stored in LEO_COLUMNS. The columns (tablespaceID, predicate. Note that we derive an adjustment factor for the tableID, columnID) uniquely identify a column (i.e. < -operator from the results of the > -operator, and we X.Price), while the Adj_factor = 0.8335 and Col_Value = apply the adjustment factor of a < -operator for the computation of the > -operator. 1 Using the example from Figure 2 and a TBSCAN on The existence of an adjustment factor indicates that we have seen a complete table scan earlier and successfully repaired an table X with the predicate Price >= 100, we can compute older statistic. 

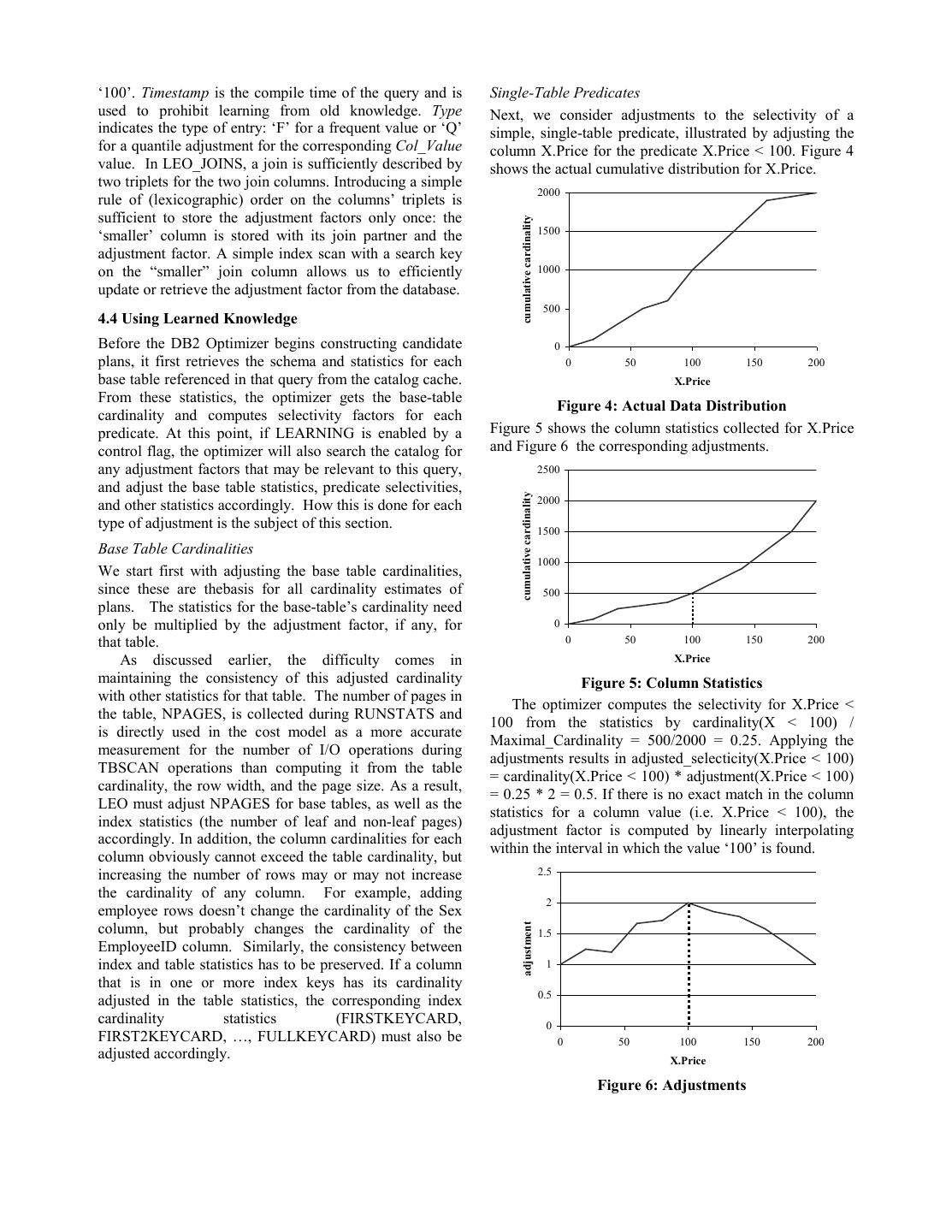
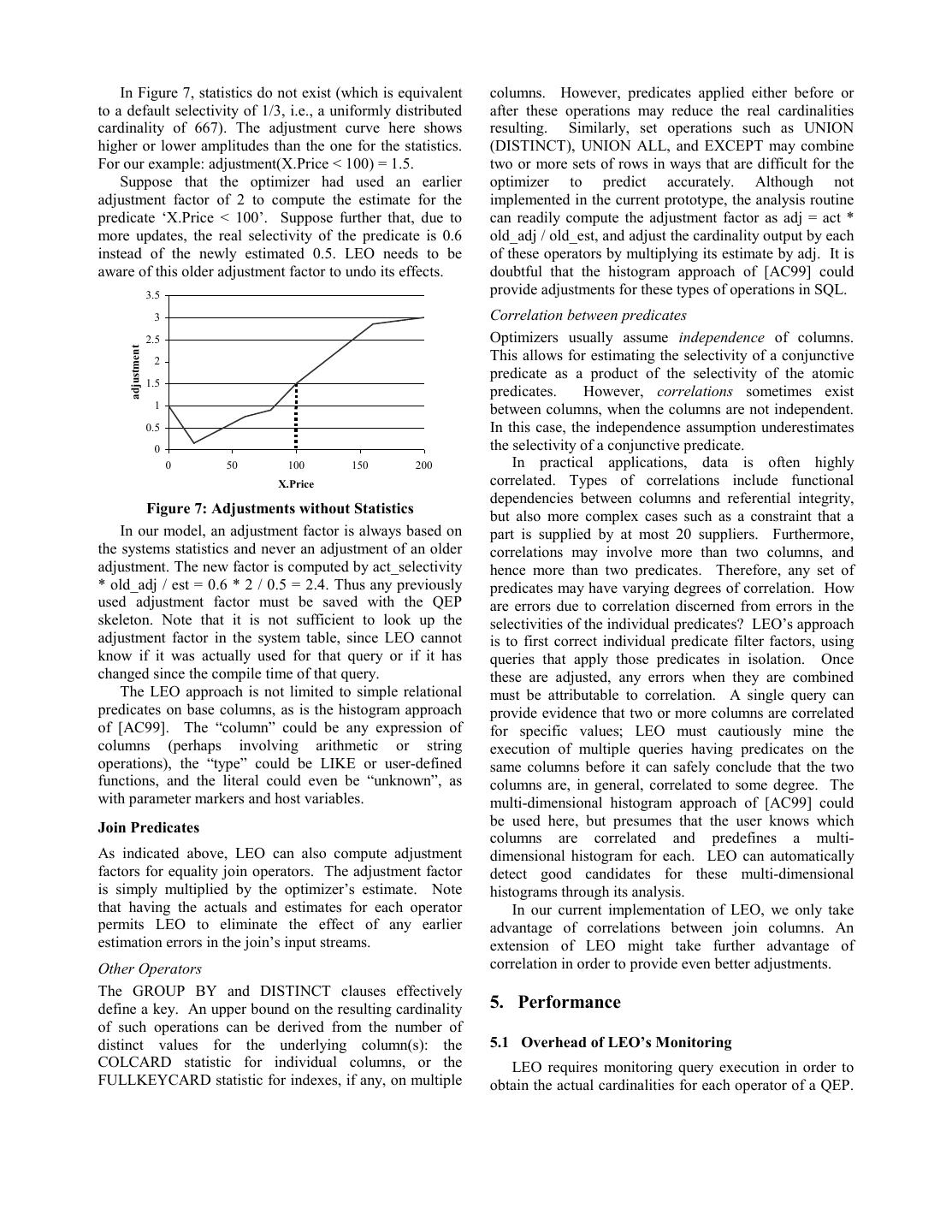
7 .‘100’. Timestamp is the compile time of the query and is Single-Table Predicates used to prohibit learning from old knowledge. Type Next, we consider adjustments to the selectivity of a indicates the type of entry: ‘F’ for a frequent value or ‘Q’ simple, single-table predicate, illustrated by adjusting the for a quantile adjustment for the corresponding Col_Value column X.Price for the predicate X.Price < 100. Figure 4 value. In LEO_JOINS, a join is sufficiently described by shows the actual cumulative distribution for X.Price. two triplets for the two join columns. Introducing a simple 2000 rule of (lexicographic) order on the columns’ triplets is sufficient to store the adjustment factors only once: the cumulative cardinality 1500 ‘smaller’ column is stored with its join partner and the adjustment factor. A simple index scan with a search key on the “smaller” join column allows us to efficiently 1000 update or retrieve the adjustment factor from the database. 500 4.4 Using Learned Knowledge Before the DB2 Optimizer begins constructing candidate 0 plans, it first retrieves the schema and statistics for each 0 50 100 150 200 base table referenced in that query from the catalog cache. X.Price From these statistics, the optimizer gets the base-table Figure 4: Actual Data Distribution cardinality and computes selectivity factors for each predicate. At this point, if LEARNING is enabled by a Figure 5 shows the column statistics collected for X.Price control flag, the optimizer will also search the catalog for and Figure 6 the corresponding adjustments. any adjustment factors that may be relevant to this query, 2500 and adjust the base table statistics, predicate selectivities, cumulative cardinality and other statistics accordingly. How this is done for each 2000 type of adjustment is the subject of this section. 1500 Base Table Cardinalities 1000 We start first with adjusting the base table cardinalities, since these are thebasis for all cardinality estimates of 500 plans. The statistics for the base-table’s cardinality need only be multiplied by the adjustment factor, if any, for 0 that table. 0 50 100 150 200 As discussed earlier, the difficulty comes in X.Price maintaining the consistency of this adjusted cardinality Figure 5: Column Statistics with other statistics for that table. The number of pages in The optimizer computes the selectivity for X.Price < the table, NPAGES, is collected during RUNSTATS and 100 from the statistics by cardinality(X < 100) / is directly used in the cost model as a more accurate Maximal_Cardinality = 500/2000 = 0.25. Applying the measurement for the number of I/O operations during adjustments results in adjusted_selecticity(X.Price < 100) TBSCAN operations than computing it from the table = cardinality(X.Price < 100) * adjustment(X.Price < 100) cardinality, the row width, and the page size. As a result, = 0.25 * 2 = 0.5. If there is no exact match in the column LEO must adjust NPAGES for base tables, as well as the statistics for a column value (i.e. X.Price < 100), the index statistics (the number of leaf and non-leaf pages) adjustment factor is computed by linearly interpolating accordingly. In addition, the column cardinalities for each within the interval in which the value ‘100’ is found. column obviously cannot exceed the table cardinality, but increasing the number of rows may or may not increase 2.5 the cardinality of any column. For example, adding 2 employee rows doesn’t change the cardinality of the Sex column, but probably changes the cardinality of the adjustment 1.5 EmployeeID column. Similarly, the consistency between index and table statistics has to be preserved. If a column 1 that is in one or more index keys has its cardinality 0.5 adjusted in the table statistics, the corresponding index cardinality statistics (FIRSTKEYCARD, 0 FIRST2KEYCARD, …, FULLKEYCARD) must also be 0 50 100 150 200 adjusted accordingly. X.Price Figure 6: Adjustments 

8 . In Figure 7, statistics do not exist (which is equivalent columns. However, predicates applied either before or to a default selectivity of 1/3, i.e., a uniformly distributed after these operations may reduce the real cardinalities cardinality of 667). The adjustment curve here shows resulting. Similarly, set operations such as UNION higher or lower amplitudes than the one for the statistics. (DISTINCT), UNION ALL, and EXCEPT may combine For our example: adjustment(X.Price < 100) = 1.5. two or more sets of rows in ways that are difficult for the Suppose that the optimizer had used an earlier optimizer to predict accurately. Although not adjustment factor of 2 to compute the estimate for the implemented in the current prototype, the analysis routine predicate ‘X.Price < 100’. Suppose further that, due to can readily compute the adjustment factor as adj = act * more updates, the real selectivity of the predicate is 0.6 old_adj / old_est, and adjust the cardinality output by each instead of the newly estimated 0.5. LEO needs to be of these operators by multiplying its estimate by adj. It is aware of this older adjustment factor to undo its effects. doubtful that the histogram approach of [AC99] could 3.5 provide adjustments for these types of operations in SQL. 3 Correlation between predicates 2.5 Optimizers usually assume independence of columns. adjustment 2 This allows for estimating the selectivity of a conjunctive predicate as a product of the selectivity of the atomic 1.5 predicates. However, correlations sometimes exist 1 between columns, when the columns are not independent. 0.5 In this case, the independence assumption underestimates 0 the selectivity of a conjunctive predicate. 0 50 100 150 200 In practical applications, data is often highly X.Price correlated. Types of correlations include functional dependencies between columns and referential integrity, Figure 7: Adjustments without Statistics but also more complex cases such as a constraint that a In our model, an adjustment factor is always based on part is supplied by at most 20 suppliers. Furthermore, the systems statistics and never an adjustment of an older correlations may involve more than two columns, and adjustment. The new factor is computed by act_selectivity hence more than two predicates. Therefore, any set of * old_adj / est = 0.6 * 2 / 0.5 = 2.4. Thus any previously predicates may have varying degrees of correlation. How used adjustment factor must be saved with the QEP are errors due to correlation discerned from errors in the skeleton. Note that it is not sufficient to look up the selectivities of the individual predicates? LEO’s approach adjustment factor in the system table, since LEO cannot is to first correct individual predicate filter factors, using know if it was actually used for that query or if it has queries that apply those predicates in isolation. Once changed since the compile time of that query. these are adjusted, any errors when they are combined The LEO approach is not limited to simple relational must be attributable to correlation. A single query can predicates on base columns, as is the histogram approach provide evidence that two or more columns are correlated of [AC99]. The “column” could be any expression of for specific values; LEO must cautiously mine the columns (perhaps involving arithmetic or string execution of multiple queries having predicates on the operations), the “type” could be LIKE or user-defined same columns before it can safely conclude that the two functions, and the literal could even be “unknown”, as columns are, in general, correlated to some degree. The with parameter markers and host variables. multi-dimensional histogram approach of [AC99] could Join Predicates be used here, but presumes that the user knows which columns are correlated and predefines a multi- As indicated above, LEO can also compute adjustment dimensional histogram for each. LEO can automatically factors for equality join operators. The adjustment factor detect good candidates for these multi-dimensional is simply multiplied by the optimizer’s estimate. Note histograms through its analysis. that having the actuals and estimates for each operator In our current implementation of LEO, we only take permits LEO to eliminate the effect of any earlier advantage of correlations between join columns. An estimation errors in the join’s input streams. extension of LEO might take further advantage of Other Operators correlation in order to provide even better adjustments. The GROUP BY and DISTINCT clauses effectively define a key. An upper bound on the resulting cardinality 5. Performance of such operations can be derived from the number of distinct values for the underlying column(s): the 5.1 Overhead of LEO’s Monitoring COLCARD statistic for individual columns, or the LEO requires monitoring query execution in order to FULLKEYCARD statistic for indexes, if any, on multiple obtain the actual cardinalities for each operator of a QEP. 

9 .Our performance measurements on a 10 GB TPC-H providing LEO with some adjustments. Figure 9 shows database [TPC00] show that for our prototype of LEO the how LEO changes the query execution plan for the query monitoring overhead is below 5% of the total query of Section 3.2 after these changes. The optimizer now execution time, and therefore may be neglected for most chooses to use a bulk method for joining X and Y for this applications. query, thus replacing the nested-loop join with a hash 4.00% join. Note that the index scan on Y was also replaced by a Serial table scan, due to the adjustments. This new plan resulted SMP in an actual execution speed-up of more than one order of 3.00% magnitude over the earlier plan executing on the same data. Est: 10 2.00% Act: 119 GROUP BY 1.00% Est: 528 Act: 1317 0.00% NL-JOIN Q2 Q14 Est: 2023 Est: 149 Figure 8: Monitoring Overhead for a 10 GB TPC-H Act: 3295 Act: 133 Database HS-JOIN Z.City = "Denver“ Est: 1149 Est: 290 IXSCAN Z Figure 8 shows the actual measurement results for the Adj. Est: 12487 Act: 12487 Adj. Est: 11083 Act: 11083 Stat: 23410 Act: 23599 overhead for TPC-H queries Q2 and Q14, measured both Y.Month = “Dec” X.Price > 100 on a single-CPU (serial) and on an SMP machine. These TBSCAN X 7%6&$1 < overheads were measured on a LEO prototype. For the Stat: 7200 Act: 21623 Stat: 2100 Act: 17949 product version, further optimizations of the monitoring code will reduce the monitoring overhead even further. Figure 9: Optimal QEP after Learning Our architecture permits dynamically enabling and Our experiments on two highly dynamic test databases disabling monitoring, on a per-query basis. If time-critical (artificial and TPC-H) showed that the adjustments applications cannot accept even this small overhead for enabled the optimizer to choose a QEP that performed up monitoring, and thus turn monitoring off, they can still to 14 times better than the QEP without adjustments, benefit from LEO, as long as other – uncritical – while LEO consumed an insignificant runtime overhead, applications monitor their query execution and thus as shown in Section 5.1. Of course, speed-ups can be even provide LEO with sufficient information. more drastic, since LEO’s adjustments can cause virtually any physical operator of a QEP to change, and may even 5.2 Benefit of Learning alter the structure of the QEP. The most prominent Adjusting outdated or incorrect information may allow the changes are table access operators (IXSCAN, TBSCAN), optimizer to choose a better QEP for a given query. join method (NLJOIN, HSJOIN, MGJOIN), and changing Depending on the difference between the new and the old the join order for multi-way joins. QEP, LEO may drastically speed-up query execution Suppose now that the database in our example has 6. Advanced Topics changed significantly since the collection of statistics: the Sales stored in table Y increased drastically in December 6.1 When to Re-Optimize and the inventory stored in table X received many updates and inserts, where most new items had a price greater than A static query is bound to a plan that the optimizer has 100. This results in an overall cardinality of more than determined during query compilation. With LEO, the plan 21623 records for X and 17949 records for Y. Suppose for a static query may change over time, since the further that these changes also introduce a skew in the adjustments might suggest an alternative plan to be better data distribution, changing the selectivities of the than the plan that is currently used for that query. The predicates X.Price > 100 and Y.Month = ‘Dec’. Finally, same holds for dynamic queries, since DB2 stores the suppose that a query referencing table X with the optimized plan for a dynamic query in a statement cache. predicate X.Price > 1502, and another query referencing Y Currently we do not support rebinding of static queries with the predicate Y.Month =’Dec’, have been executed, or flushing the statement cache because of learned knowledge. It remains future work to investigate whether and when re-optimization of a query should take place. 2 Note that it is not necessary to run a query with exactly the The trade-off between re-optimization and improved predicate X.Price > 100, since LEO performs interpolation for runtime must be weighed in order to be sure that re- histograms. Thus an adjustment for X.Price >150 is also be optimization will result in improved query performance. useful for a query X.Price > 100. 

10 .6.2 Learning Other Information LEO’s adjustments to change a query’s plan dynamically Learning and adapting to a dynamic environment is not during its execution in a robust, industrial-strength way. restricted to cardinalities and selectivities. Using a Acknowledgements feedback loop, many configuration parameters of a DBMS can be made self-tuning. If, for instance, the The authors thank Kwai Wong for her help with the DBMS detects by query feedback that a sort operation measurements of the LEO runtime overhead, and could not be performed in main memory, the sort heap Ashutosh Singh and Eric Louie for systems support. size could be adjusted in order to avoid external sorting for future sort operations. In the same way, buffer pools Bibliography for indexes or tables could be increased or decreased AC99 A. Aboulnaga and S. Chaudhuri, Self-tuning according to a previously seen workload. This is Histograms: Building Histograms Without Looking especially interesting for resources that are assigned on a at Data, SIGMOD, 1999 per-user basis: Instead of assuming uniformity, buffer ARM89 R. Ahad, K.V.B. Rao, and D. McLeod, On pools or sort heaps could be maintained individually per Estimating the Cardinality of the Projection of a user. If dynamic adaptation is possible even during Database Relation, TODS 14(1), pp. 28-40. connections, open but inactive connections could transfer CR94 C. M. Chen and N. Roussopoulos, Adaptive Selectivity Estimation Using Query Feedback, resources to highly active connections. SIGMOD, 1994 Another application of adjustments is to “debug” the Gel93 A. Van Gelder, Multiple Join Size Estimation by cost model of the query optimizer: If – despite correct Virtual Domains, PODS, pp. 180-189. base statistics – the cost prediction for a query is way off, GMP97 P. B. Gibbon, Y. Matias and V. Poosala, Fast analyzing the adjustment factors permits locating which Incremental Maintenance of Approximate of the assumptions of the cost model are violated. Histograms, VLDB, 1999 Physical parameters such as the network rate, disk HS93 P. Haas and A. Swami, Sampling-Based Selectivity access time, or disk transfer rate are usually considered to Estimation for Joins - Using Augmented Frequent be constant after an initial set-up. However, monitoring Value Statistics, IBM Research Report, 1993 IBM00 DB2 Universal Data Base V7 Administration and adjusting the speed of disks and networks enables the Guide, IBM Corp., 2000 optimizer to adjust dynamically to the actual workload IC91 Y.E. Ioannidis and S. Christodoulakis. On the and use the effective rate. Propagation of Errors in the Size of Join Results, SIGMOD, 1991 7 Conclusions KdeW98 N. Kabra and D. DeWitt, Efficient Mid-Query Re- Optimization of Sub-Optimal Query Execution LEO provides a general mechanism for an optimizer Plans, SIGMOD, 1998 to actually learn from its mistakes by adjusting its Lyn88 C. Lynch, Selectivity Estimation and Query cardinality and other estimates using the actuals from the Optimization in Large Databases with Highly execution of previous queries having similar predicates. Skewed Distributions of Column Values, VLDB, Regardless of the source of error – old statistics, invalid 1988 assumptions, inadequate modeling, unknown literals, etc. PI97 V. Poosala and Y. Ioannidis, Selectivity Estimation without the attribute value independence – LEO can detect and correct the mistake for any kind of assumption, VLDB, 1997 operation that changes the cardinality, at any point in a PIHS96 V. Poosala, Y. Ioannidis, P. Haas, and E. Shekita, plan. This is a far more general mechanism than multi- Improved histograms for selectivity estimation of dimensional histograms, which are limited to local range predicates, SIGMOD. 1996, pp. 294-305 predicates on columns of a base table. Our performance SAC+79 P.G. Selinger, M. M. Astrahan, D. D. Chamberlin, measurements have demonstrated that LEO can improve R. A. Lorie, T. G. Price, Access Path Selection in a cardinality estimates by orders of magnitude, changing Relational Database Management System, plans to improve performance by orders of magnitude, SIGMOD 1979, pp. 23-34 while adding less than 5% overhead to execution time SS94 A. N. Swami, K. B. Schiefer, On the Estimation of Join Result Sizes, EDBT 1994, pp. 287-300 when monitoring actuals. We feel that LEO provides a TPC00 Transaction Processing Council, TPC-H Rev. 1.2.1 major step forward in improving the quality of query specification, 2000 optimization and reducing the need for “tuning” of UFA98 T. Urhan, M.J. Franklin and L. Amsaleg, Cost- problem queries, a major contributor to cost of ownership. based Query Scrambling for Initial Delays, Our future work includes completing the SIGMOD, 1998 implementation of LEO’s adjustments for all types of predicates, measuring the benefit on a realistic set of user queries, finding conclusive ways to discern correlation among predicates, applying LEO’s approach to parameters other than cardinality, and possibly using