07数据结构---图

1 . 第七章 图 东南大学计算机学院 方效林 方效林 本课件借鉴了清华大学殷人昆老师 和哈尔滨工业大学张岩老师的课件 

2 . 本章主要内容  图的基本概念  图的存储表示  图的遍历与连通性  最小生成树  最短路径 2 

3 . 图的基本概念  定义  图是由顶点及顶点之间的关系集合组成的数据结构 Graph = ( V, E )  V 是顶点的有穷非空集， V={x | x∈ 某个对象 }  E 是顶点之间关系，称为边 (edge) 的有穷非穷 集， E={(x,y) | x,y∈V} 3 

4 . 图的基本概念  有向图与无向图  有向图中，顶点对 (x,y) 是有序的  无向图中，顶点对 (x,y) 是无序的  完全图  n 个顶点的无向图有 n(n-1)/2 条边 , 该图为完全图  n 个顶点的有向图有 n(n-1) 条边 , 该图为完全有向 0 图 0 0 1 2 6 8 1 2 1 3 4 5 6 2 7 3 完全无向图 4 无向图 ( 自由树 ) 有向图 完全有向图 

5 . 图的基本概念  邻接顶点  (u, v) 是 E 中的一条边，则称 u 与 v 互为邻接顶点  子图  设有两个图 G ＝ (V, E) 和 G’ ＝ (V’, E’) 。若 若 V’ V 且 E’E, 则称 G’ 是 G 的子图 0 0 0 子图 1 2 1 1 2 1 2 3 3 3 3  权：边附带的权重，称这样的图称为带权图 5 

6 . 图的基本概念  顶点 v 的度  与 v 为端点的边条数，记作 D(v)  入度：有向图中 , 以 v 为终点的边的条数 , 记作 ID(v)  出度：有向图中 , 以 v 为始点的边的条数 , 记作 OD(v)  有向图中 v 的度为入度与出度的和  路径  图 G ＝ (V, E) 中 , 从顶点 vi 出发 , 沿一些边经过一些 顶点 vp1, vp2, …, vpm ，到达顶点 vj 。若 则称顶点序列 (vi vp1 vp2 ... vpm vj) 为从顶点 vi 到顶点 vj 的路径。若 它经过的 边 (vi, vp1) 、 (vp1, vp2) 、 ... 、 (vpm, vj) 应是属于 E 的边 。若 6 

7 . 图的基本概念  路径长度  非带权图的路径长度是指此路径上边的条数  带权图的路径长度是指路径上各边的权之和  简单路径  路径上各顶点 v1,v2,...,vm 均不互相重复  回路  路径上第一个顶点 v1 与最后一个顶点 vm 重合 7 

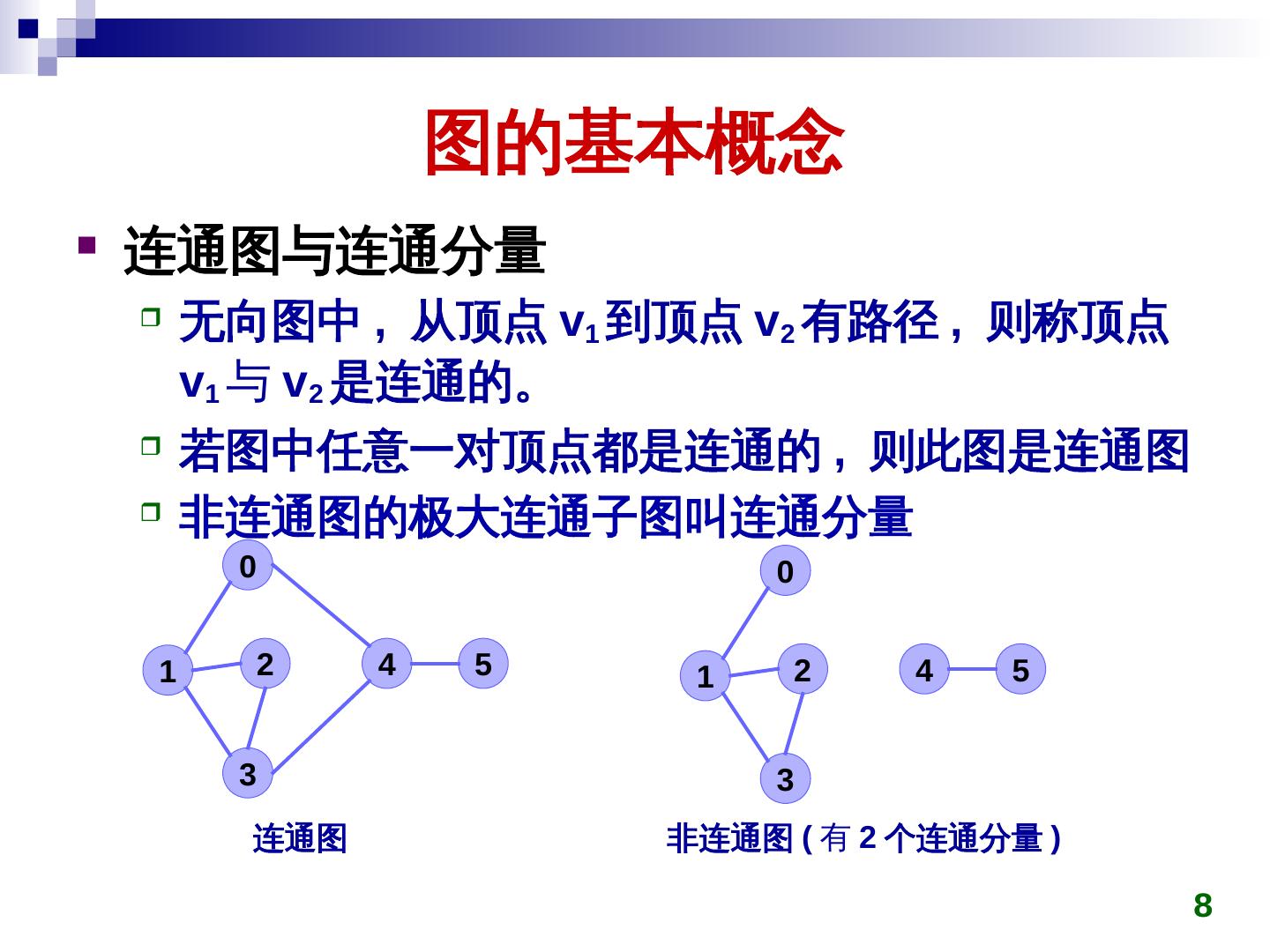
8 . 图的基本概念  连通图与连通分量  无向图中 , 从顶点 v1 到顶点 v2 有路径 , 则称顶点 v1 与 v2 是连通的。若  若图中任意一对顶点都是连通的 , 则此图是连通图  非连通图的极大连通子图叫连通分量 0 0 1 2 4 5 1 2 4 5 3 3 连通图 非连通图 ( 有 2 个连通分量 ) 8 

9 . 图的基本概念  强连通图与强连通分量  在有向图中 , 若对于每一对顶点 vi 和 vj, 都存在一 条从 vi 到 vj 和从 vj 到 vi 的路径 , 则称此图是强连 通图  非强连通图的极大强连通子图叫做强连通分量  生成树  一个连通图的生成树是其极小连通子图，在 n 个 顶点的情形下，有 n-1 条边。若 9 

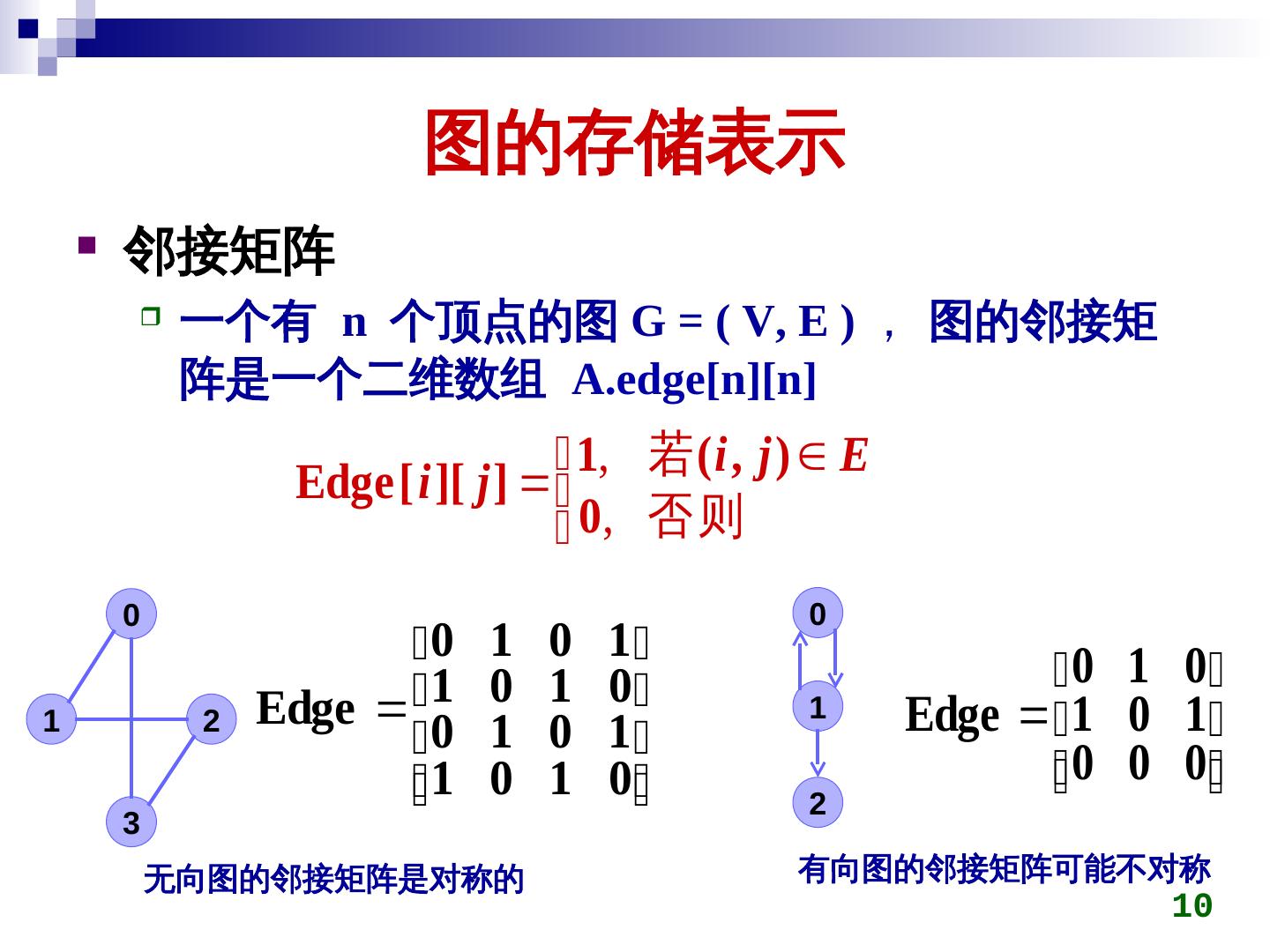
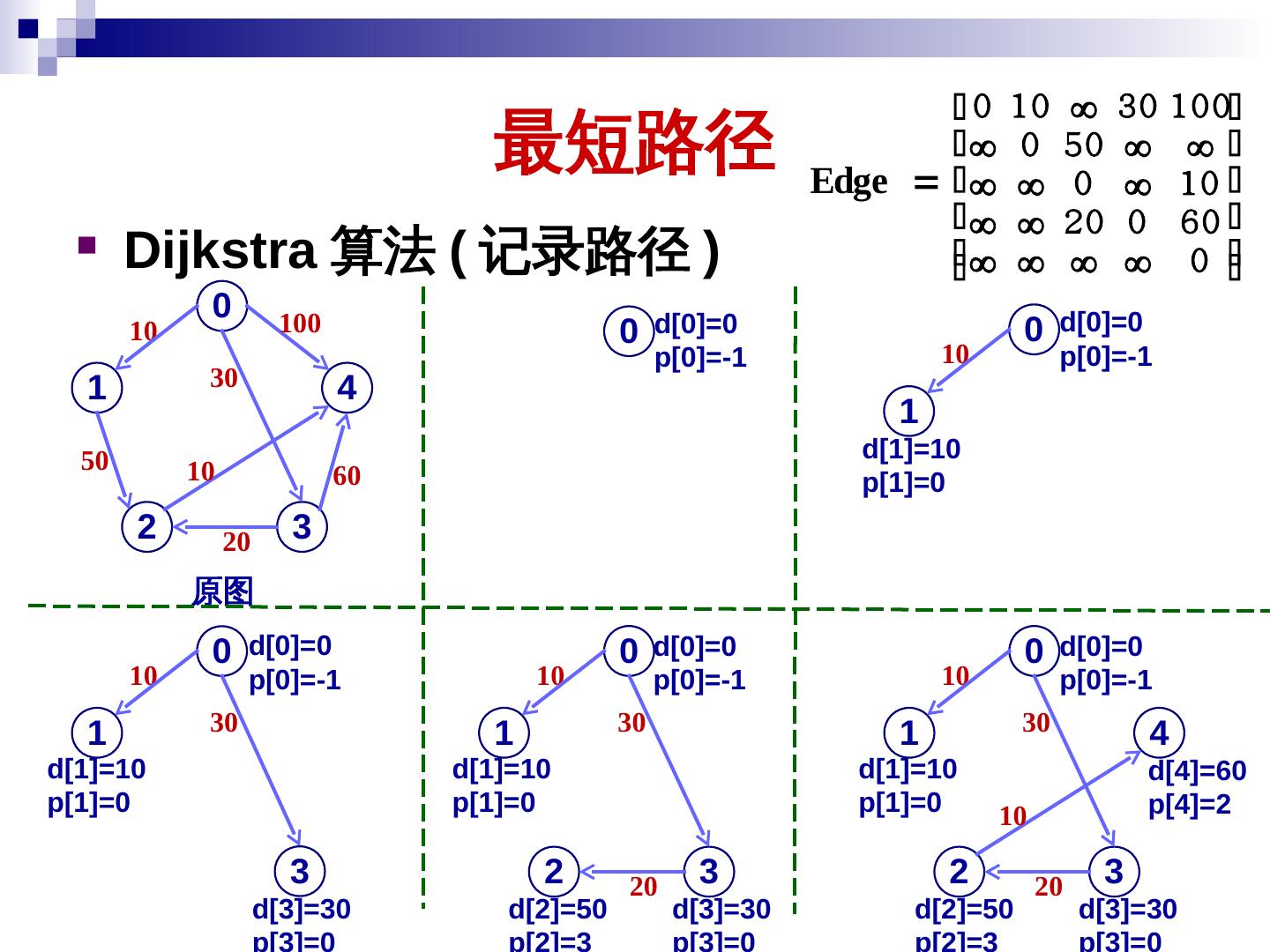
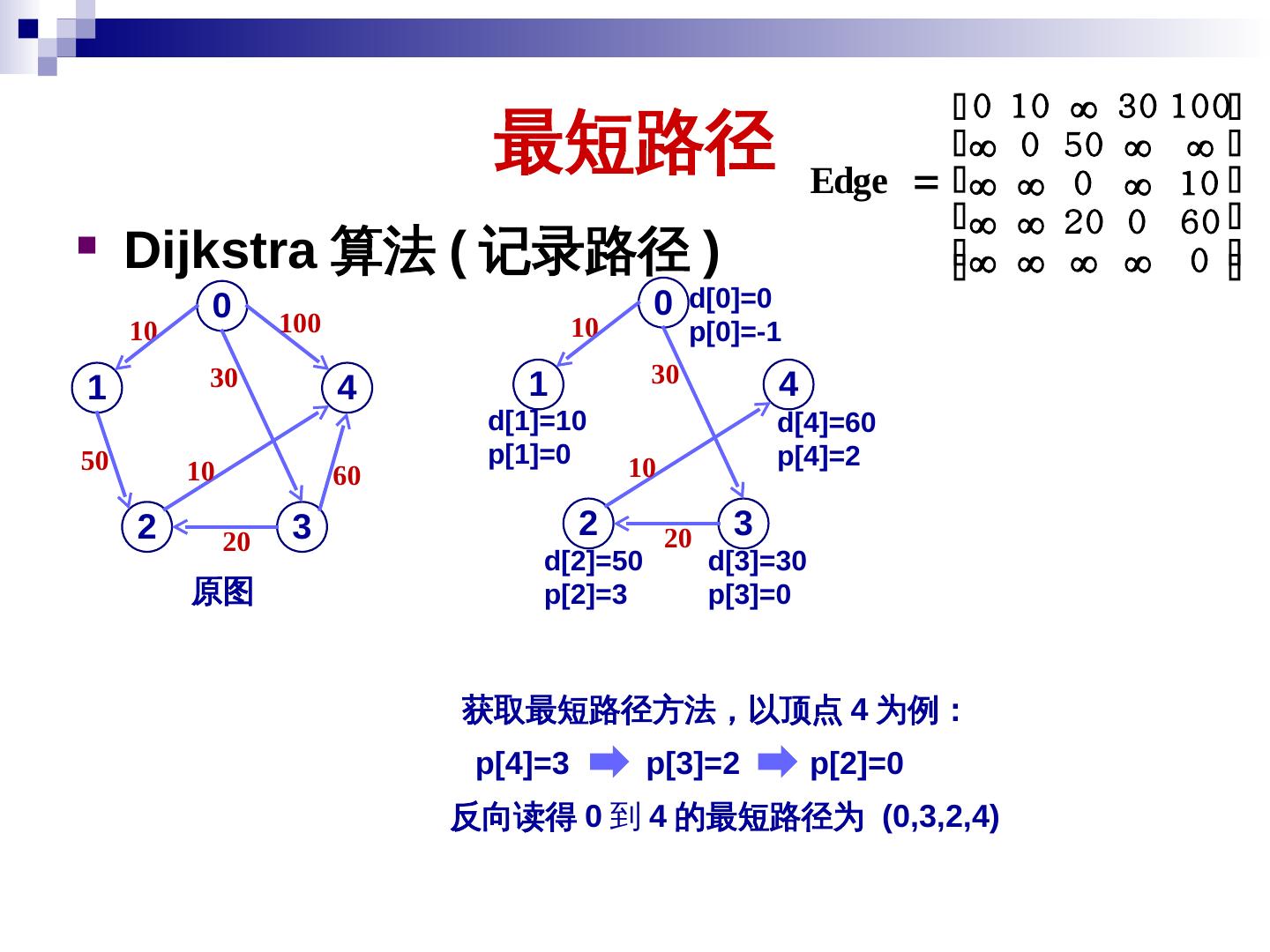
10 . 图的存储表示  邻接矩阵  一个有 n 个顶点的图 G = ( V, E ) ， 图的邻接矩 阵是一个二维数组 A.edge[n][n]  1, 若 ( i , j )  E Edge[ i ][ j ]    0, 否 则 0 0 0 1 0 1 0 1 0 1 2 Edge 10 0 1 1 0 0 1 1 Edge 1 0 1   1 0 1 0 0 0 0 2 3 无向图的邻接矩阵是对称的 有向图的邻接矩阵可能不对称 10 

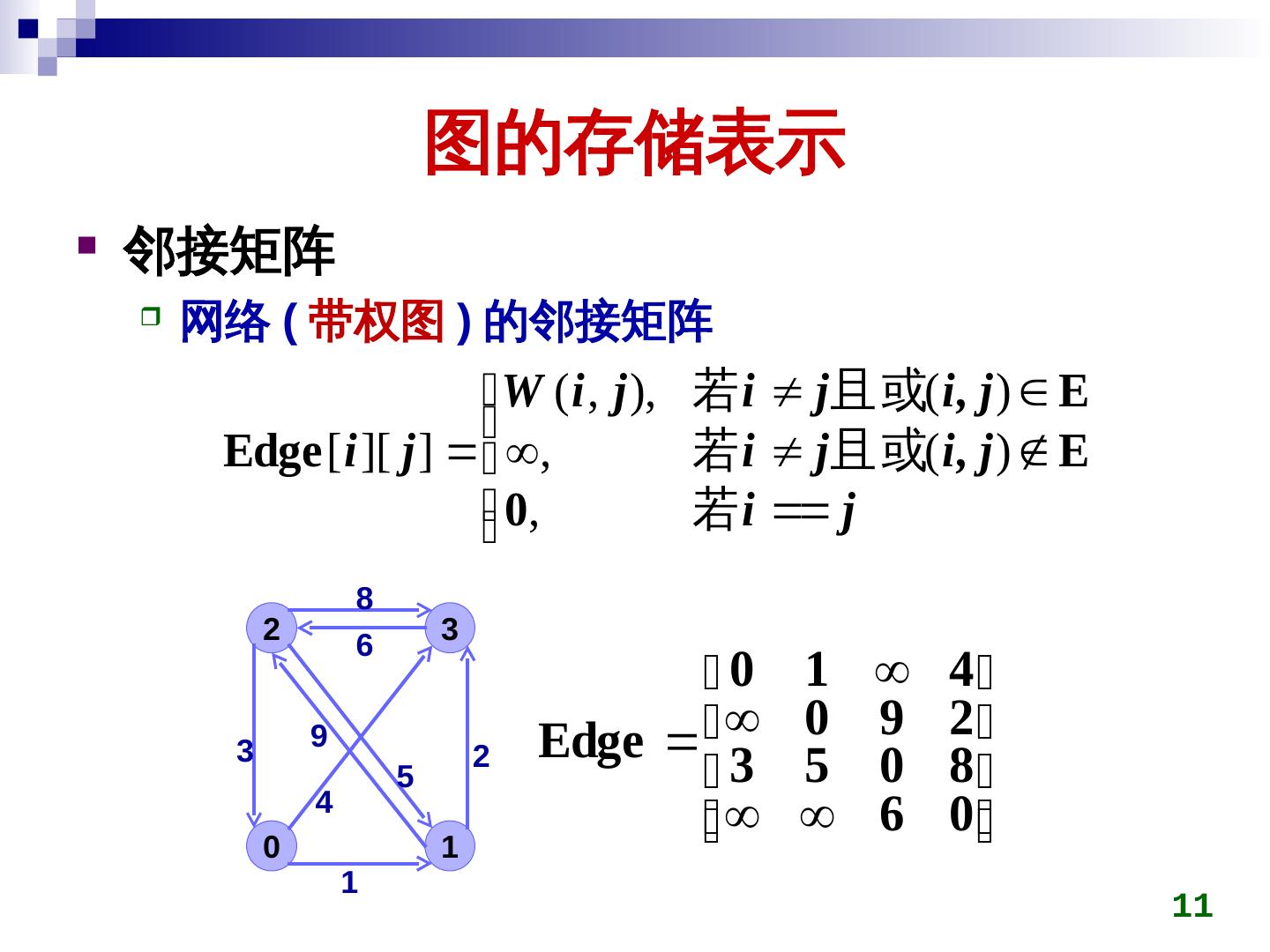
11 . 图的存储表示  邻接矩阵  网络 ( 带权图 ) 的邻接矩阵  W ( i , j ), 若 i  j且 或( i, j )  E  Edge [ i ][ j ]  , 若 i  j且 或( i, j )  E  0, 若 i  j 8 2 6 3 0 1  4 3 9 Edge   0 9 2 5 2 3 5 0 8 0 4 1   6 0 1 11 

12 . 图的存储表示  邻接表  无向图的邻接表 dest link dest link A data link 1 2  0 A 0 3  B D 1 B 2 C 0  C 3 D 1  顶点数组 链接结点 dest 保存的是邻接顶点的下标 12 

13 . 图的存储表示  邻接表  有向图的邻接表和逆邻接表 data link dest link A 1  0 A dest link 1 B 0 2  B 2 C  C 邻接表 ( 出边表 ) data link dest link 0 A 1  1 B 0  2 C 2  13 逆邻接表 ( 入边表 ) 

14 . 图的存储表示 8 D C  网络 ( 带权图 ) 的邻接表 6 9 3 2 5 4 A B dest cost link dest cost link 1 data link 1 1 2 4  0 A 2 2 3 9  1 B 2 C 3 6  3 D 0 3 1 5 2 8  邻接表 ( 出边表 ) 14 

15 . 图的遍历  从给定顶点出发，沿某些边遍历图中所有顶点 一次且仅一次  使用辅助数组 visited[ ] 标识顶点是否被访问 过  visited[ ] 初始为 0  访问过后标识为 1 15 

16 . 图的遍历  遍历方式  深度优先遍历 DFS (Depth First Search)  广度优先遍历 BFS (Breadth First Search) 16 

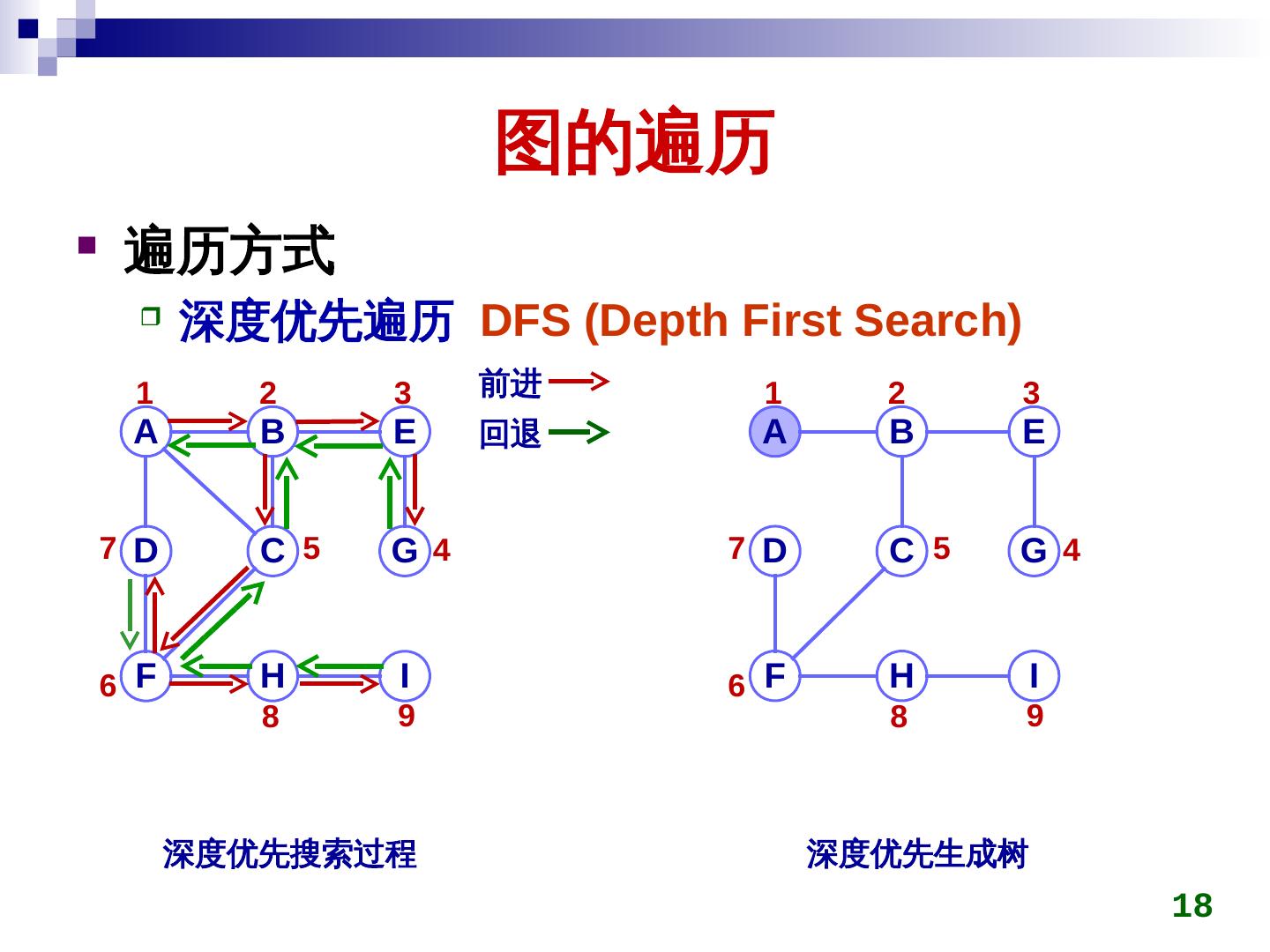
17 . 图的遍历  遍历方式  深度优先遍历 DFS (Depth First Search)  从顶点 v1 出发，访问任一未被访问的邻接顶点 v2;  再从顶点 v2 出发，访问任一未被访问的邻接顶点 v3;  再从顶点 v3 出发，… ，如此进行下去，直到所有邻 接顶点都被访问过为止  退回一步到刚被访问的顶点，看是否有未被访问的邻 接顶点。若  若有，则继续访问  否则，再退回一步  直到所有顶点都被访问 17 

18 . 图的遍历  遍历方式  深度优先遍历 DFS (Depth First Search) 1 2 3 前进 1 2 3 A B E 回退 A B E 7 D C 5 G 4 7 D C 5 G 4 6 F H I 6 F H I 8 9 8 9 深度优先搜索过程 深度优先生成树 18 

19 . 图的遍历  遍历方式  广度优先遍历 BFS (Breadth First Search)  从起始顶点 v 出发，依次访问 v 的未被访问的邻接顶 点 w 1, w 2, … , w m  顺序访问 w1, w2, … , wm 的所有未被访问的邻接顶点 , 以此类推，直到所有顶点都被访问 19 

20 . 图的遍历  遍历方式  广度优先遍历 BFS (Breadth First Search) 1 2 5 1 2 5 A B E A B E 4 D 3 C G 7 4 D 3 C G 5 6 F H I 6 F H I 8 9 8 9 广度优先搜索过程 广度优先生成树 20 

21 .作业： n 个顶点无向图，邻接矩阵形式存储在矩阵 Edge[N][N] ， 用 visited 记录是否访问过，初始时 visited[N]={0} 写出深度优先遍历程序： DFS(0, Edge[][]) { } 写出广度优先遍历程序： BFS(0, Edge[][]) { } 21 

22 . 图的遍历  遍历方式  深度优先遍历 DFS (Depth First Search)  回溯算法  广度优先遍历 BFS (Breadth First Search)  分层算法 22 

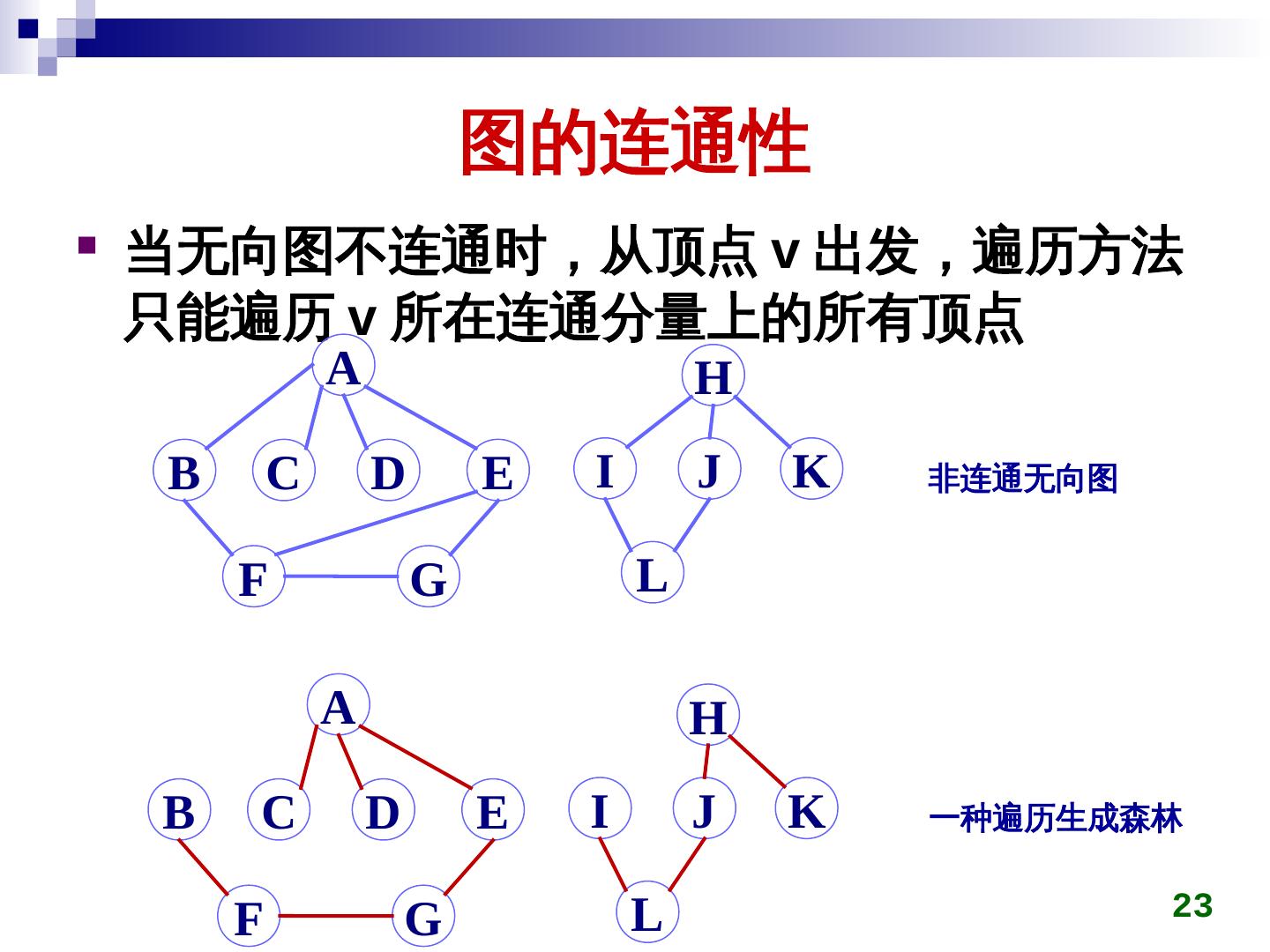
23 . 图的连通性  当无向图不连通时，从顶点 v 出发，遍历方法 只能遍历 v 所在连通分量上的所有顶点 A H B C D E I J K 非连通无向图 F G L A H B C D E I J K 一种遍历生成森林 F G L 23 

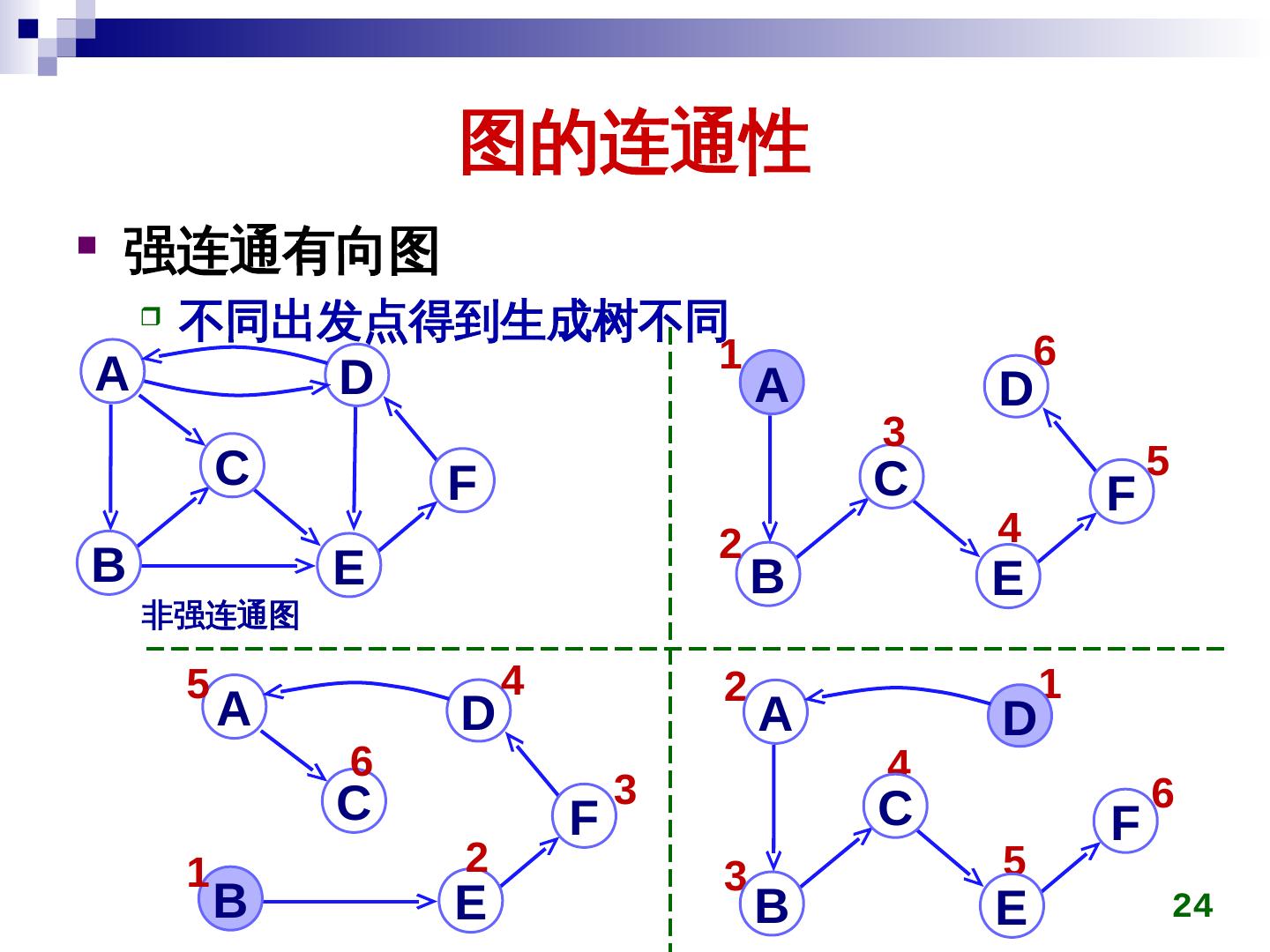
24 . 图的连通性  强连通有向图  不同出发点得到生成树不同 1 6 A D A D 3 C C 5 F F 2 4 B E B E 非强连通图 5 4 2 1 A D A D 6 4 C 3 C 6 F F 1 2 3 5 B E B E 24 

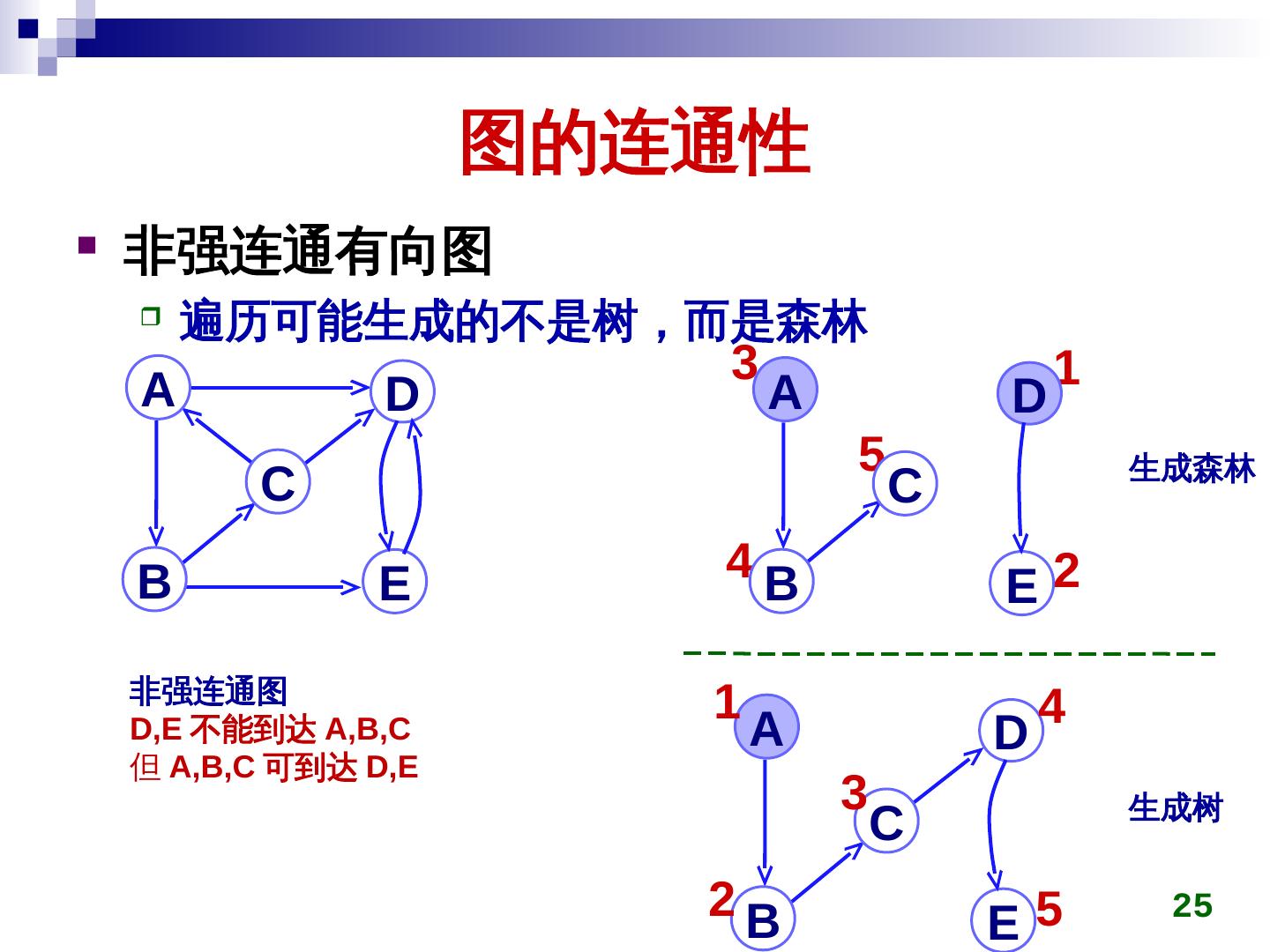
25 . 图的连通性  非强连通有向图  遍历可能生成的不是树，而是森林 3 1 A D A D 5 生成森林 C C 4B B E E2 非强连通图 1 4 D,E 不能到达 A,B,C A D 但 A,B,C 可到达 D,E 3 生成树 C 2B E5 25 

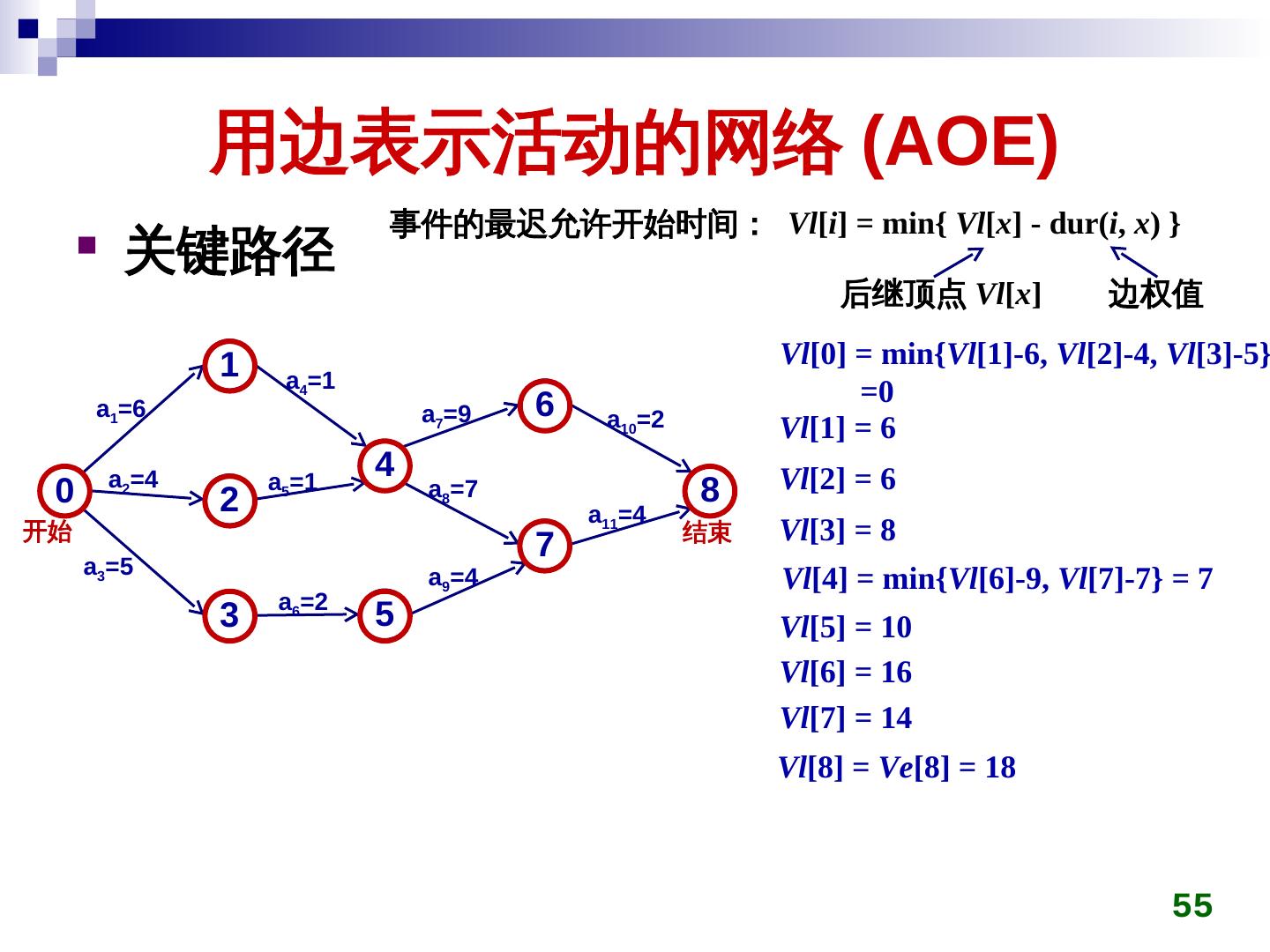
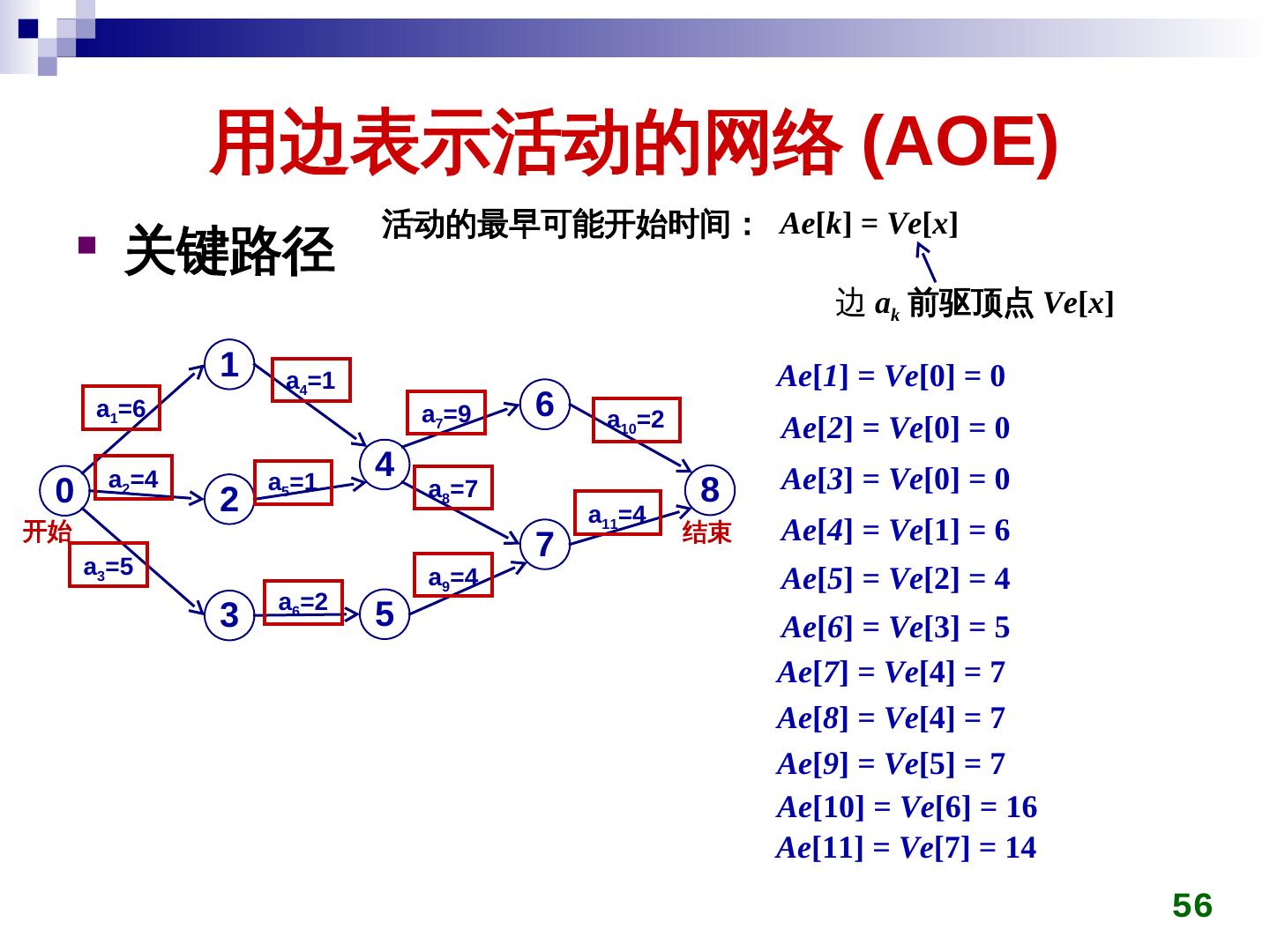
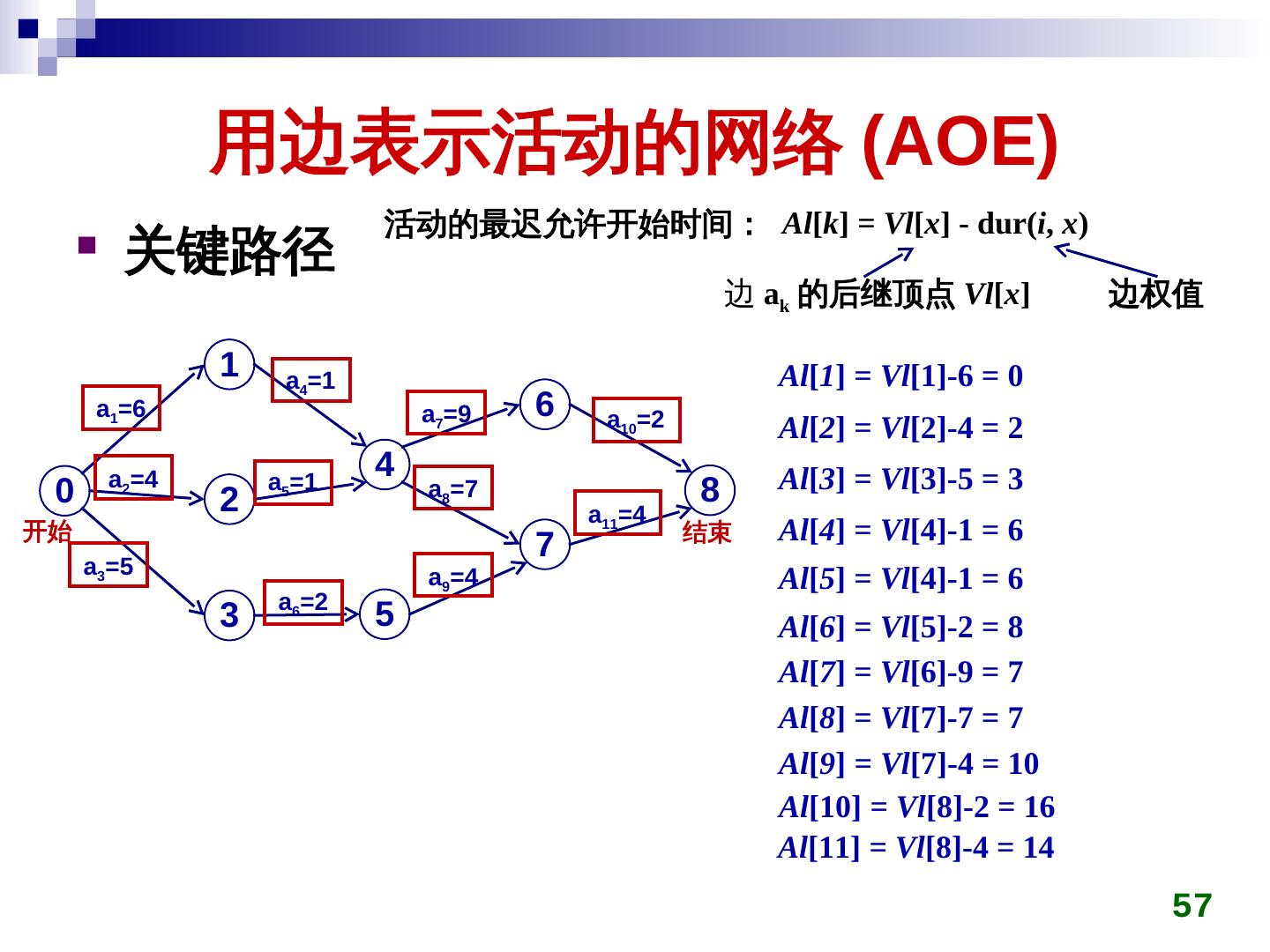
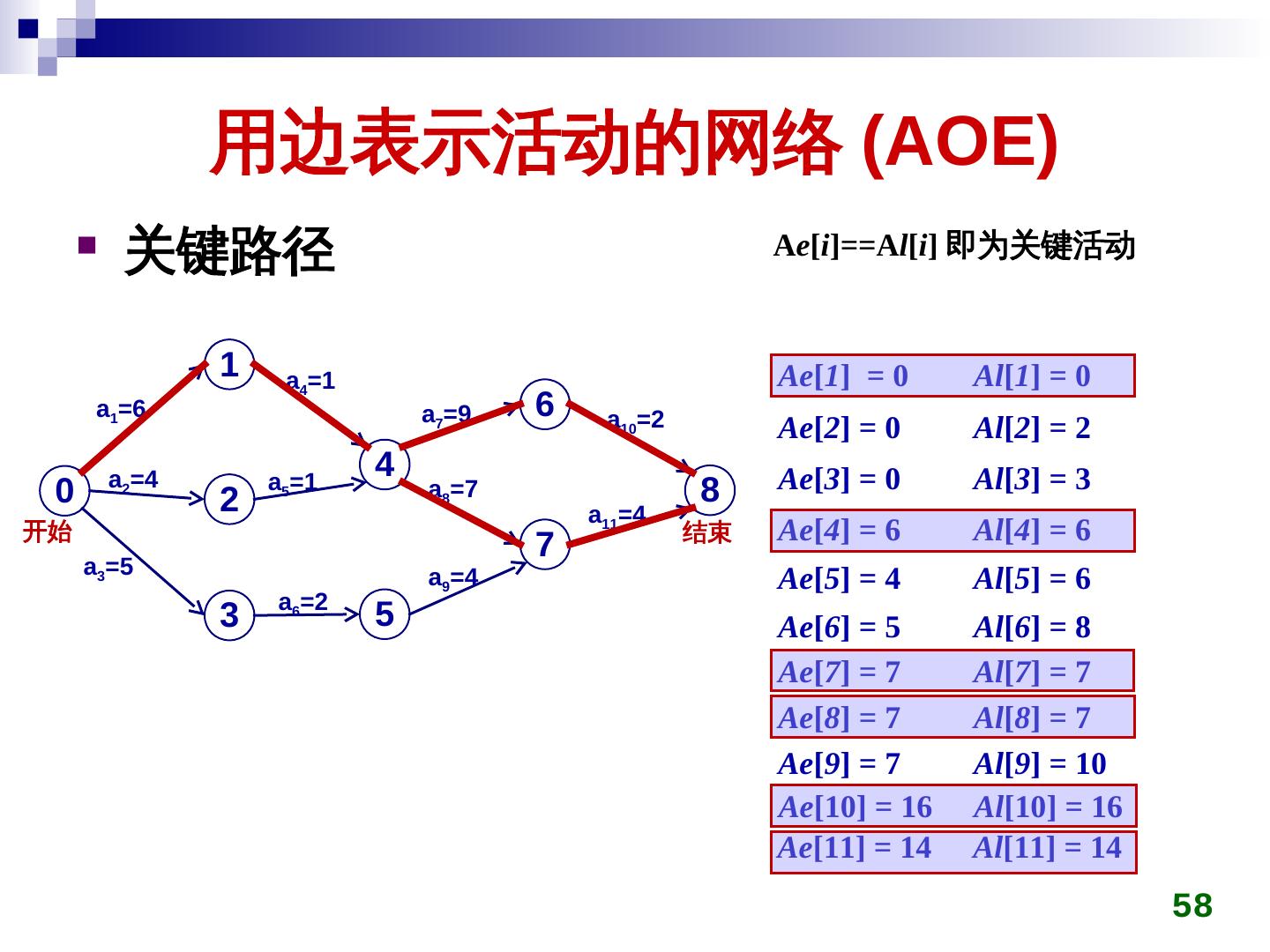
26 . 最小生成树  在连通带权图上构造一棵生成树，使得该树上 边权值的总和最小  连通带权图  生成树 (n 个顶点， n-1 条边，无回路 )  边的权值总和最小 26 

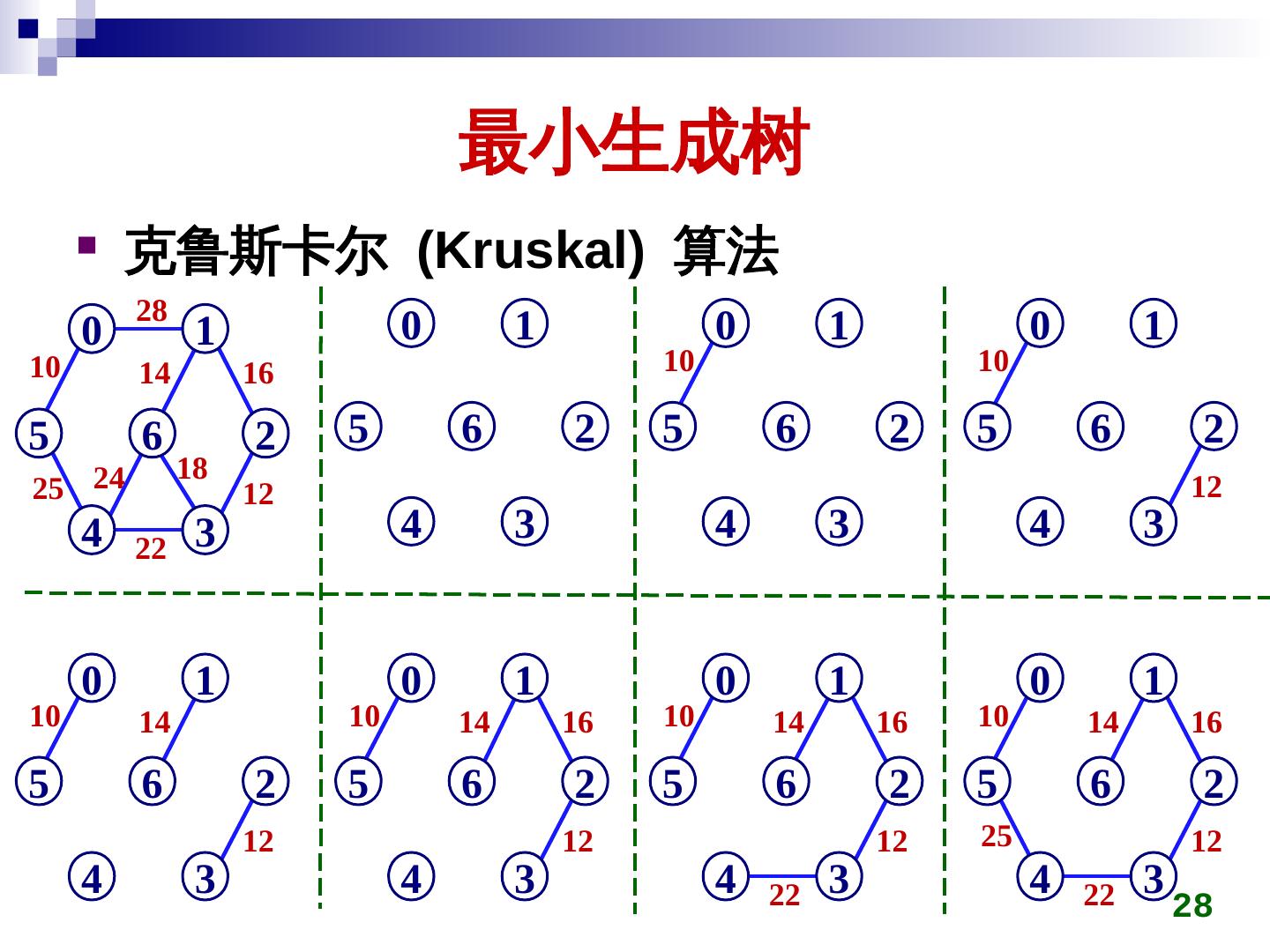
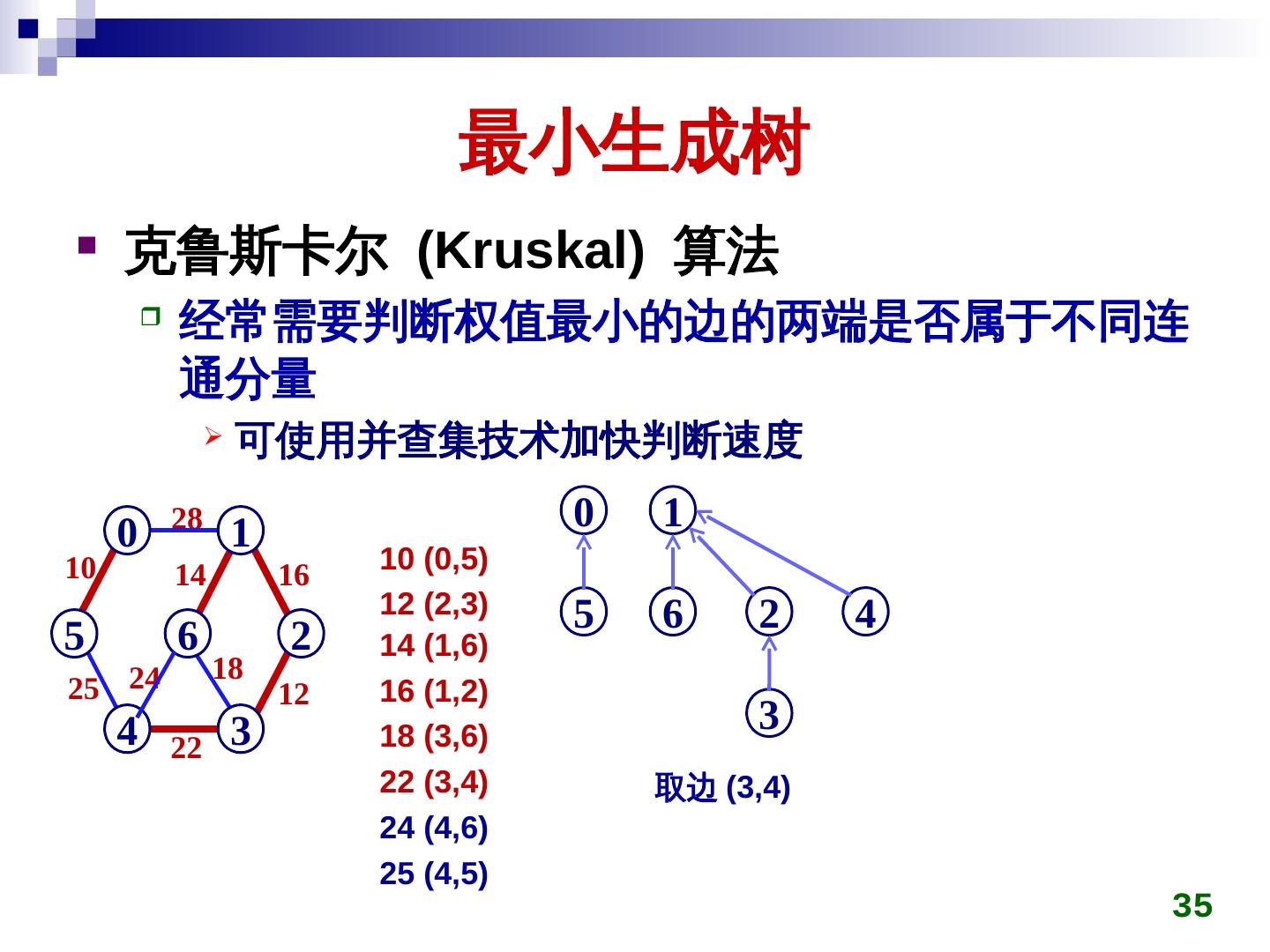
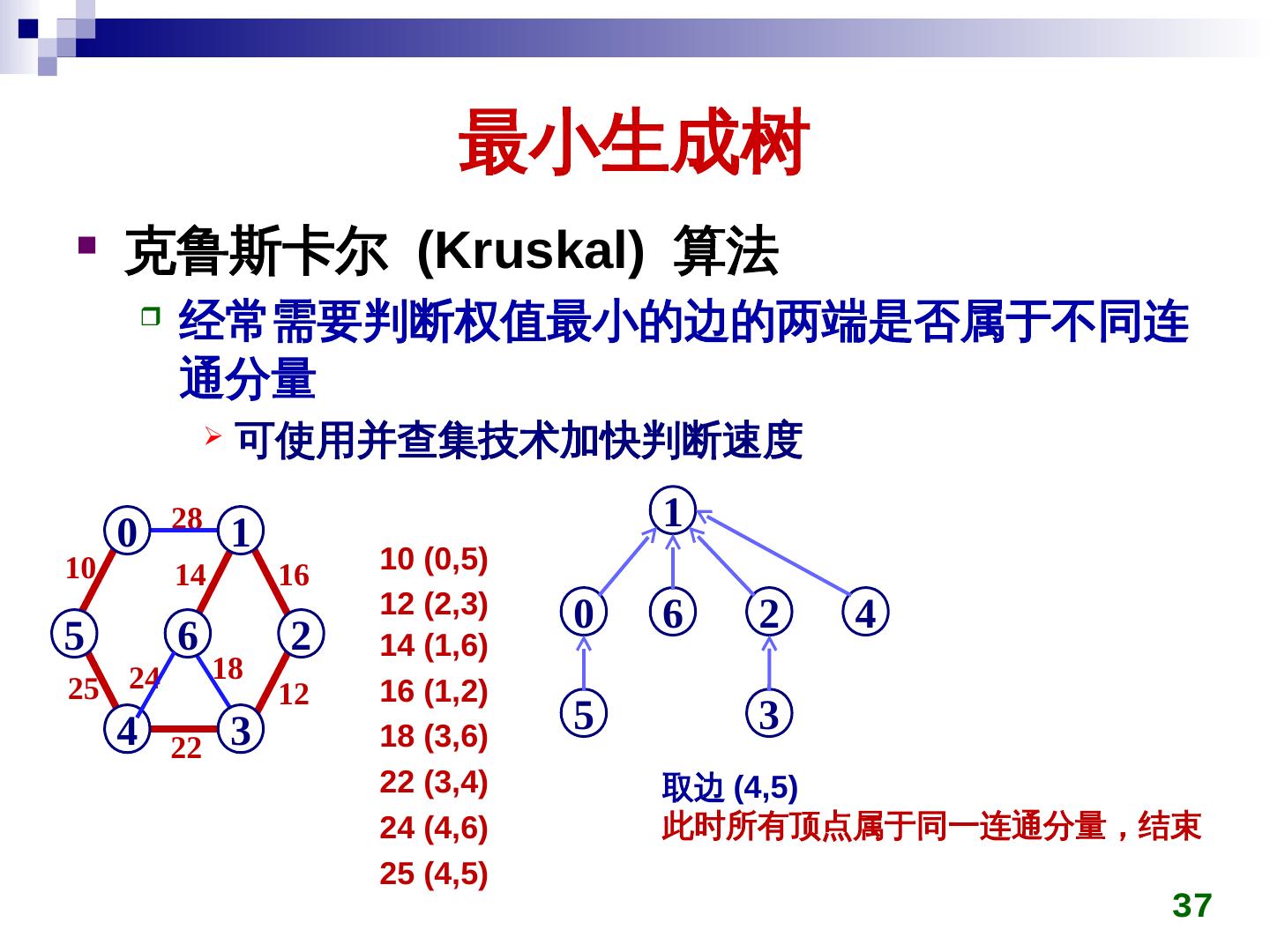
27 . 最小生成树  克鲁斯卡尔 (Kruskal) 算法  初始时所有顶点自成一连通分量  在图上选权值最小的边 emin ，判断 emin 两端点是否 属于不同连通分量 ci,cj  若是，将 ci,cj 用 emin 连接成同一个连通分量  否则，舍弃 emin  重复上一过程，直到所有顶点在同一连通分量 27 

28 . 最小生成树  克鲁斯卡尔 (Kruskal) 算法 28 0 1 0 1 0 1 0 1 10 14 16 10 10 5 6 2 5 6 2 5 6 2 5 6 2 18 25 24 12 12 4 3 4 3 4 3 4 3 22 0 1 0 1 0 1 0 1 10 14 10 14 16 10 14 16 10 14 16 5 6 2 5 6 2 5 6 2 5 6 2 12 12 12 25 12 4 3 4 3 4 22 3 4 22 3 28 

29 . 最小生成树  克鲁斯卡尔 (Kruskal) 算法  经常需要判断权值最小的边的两端是否属于不同连 通分量  可使用并查集技术加快判断速度 28 0 1 2 3 4 5 6 0 1 10 10 (0,5) 14 16 初始时 12 (2,3) 5 6 2 14 (1,6) 18 25 24 12 16 (1,2) 4 22 3 18 (3,6) 22 (3,4) 24 (4,6) 25 (4,5) 29