- 快召唤伙伴们来围观吧
- 微博 QQ QQ空间 贴吧
- 文档嵌入链接
- 复制
- 微信扫一扫分享
- 已成功复制到剪贴板
02算法设计与分析---算法分析的数学基础
展开查看详情
1 .东南大学计算机学院 方效林 第一章 算法分析的数学基础
2 .本章内容 复杂性函数的阶 和的估计与界限 递归方程 2
3 .一些记号 表示小于等于 的最大整数 表示大于等于 的最小整数 , 3
4 .复杂性函数的阶 渐近复杂性 当输入规模趋于极限情形时 ( 相当大 ) 的复杂性 表示复杂性 阶 的三个记号 T(n)=O(f(n)) 若存在 c > 0 ,和正整数 n 0 ≥1 ,使得当 n≥n 0 时,有 T(n)≤c*f(n) 成立 。 给出算法复杂度的上界,不可能比 c*f(n) 更大 e.g. T(n)=3n 3 +2n 2 ,取 c=5 , n 0 =1 , f(n)=n 3 ,则当 n≥n 0 (=1) 时,有 3n 3 +2n 2 ≤5n 3 . ∴T(n)= O(n 3 ) 4
5 .复杂性 函数 的 阶 渐近复杂性 当输入规模趋于极限情形时 ( 相当大 ) 的复杂性 表示复杂性 阶 的三个记号 T(n)=Ω(f(n)) 若存在 c > 0 ,和正整数 n 0 ≥1 ,使得当 n≥n 0 时, 有 T(n)≥c*f(n) 成立。 给出算法复杂度的下界,不可能比 c*f(n) 更小 e.g. T(n)=3n 3 +2n 2 ,取 c=3 , n 0 =1 , f(n)=n 3 ,则当 n≥n 0 (=1) 时,有 3n 3 +2n 2 ≥3n 3 , ∴T(n)=Ω(n 3 ) 5
6 .复杂性 函数 的 阶 渐近复杂性 当输入规模趋于极限情形时 ( 相当大 ) 的复杂性 表示复杂性 阶 的三个记号 T(n)= (f(n)) 若存在 c 1 ,c 2 >0 ,和正整数 n 0 ≥1 ,使得当 n≥n 0 时,总有 T(n)≤c 1 *f(n) 且 T(n)≥c 2 *f(n) 成立,即 T(n)=O(f(n)) 与 T(n)=Ω(f(n)) 都成立。 给出了算法时间复杂度的上界 和 下界 e.g.T (n)= 3n 3 +2n 2 , c 1 =5 ,取 c 2 =3 , n 0 =1 , f(n)=n 3 ,则当 n≥n 0 (=1) 时,有 3n 3 +2n 2 ≤5n 3 及 3n 3 +2n 2 ≥3n 3 (无穷多个), ∴T(n)= (n 3 ) 6
7 .多项式时间与指数时间 设每秒可做某基本运算 10 9 次, n=60 两个结论 多项式时间的算法互相之间虽有差距,一般可接受 指数量级时间的算法对于较大的 n 无实用价值 7 算法 1 算法 2 算法 3 算法 4 算法 5 算法 6 复杂度 n n 2 n 3 n 5 2 n 3 n 运算时 6*10 -8 s 3.6*10 -6 s 2.16*10 -4 s 0.013min 3.66 世纪 1.3*10 13 世纪
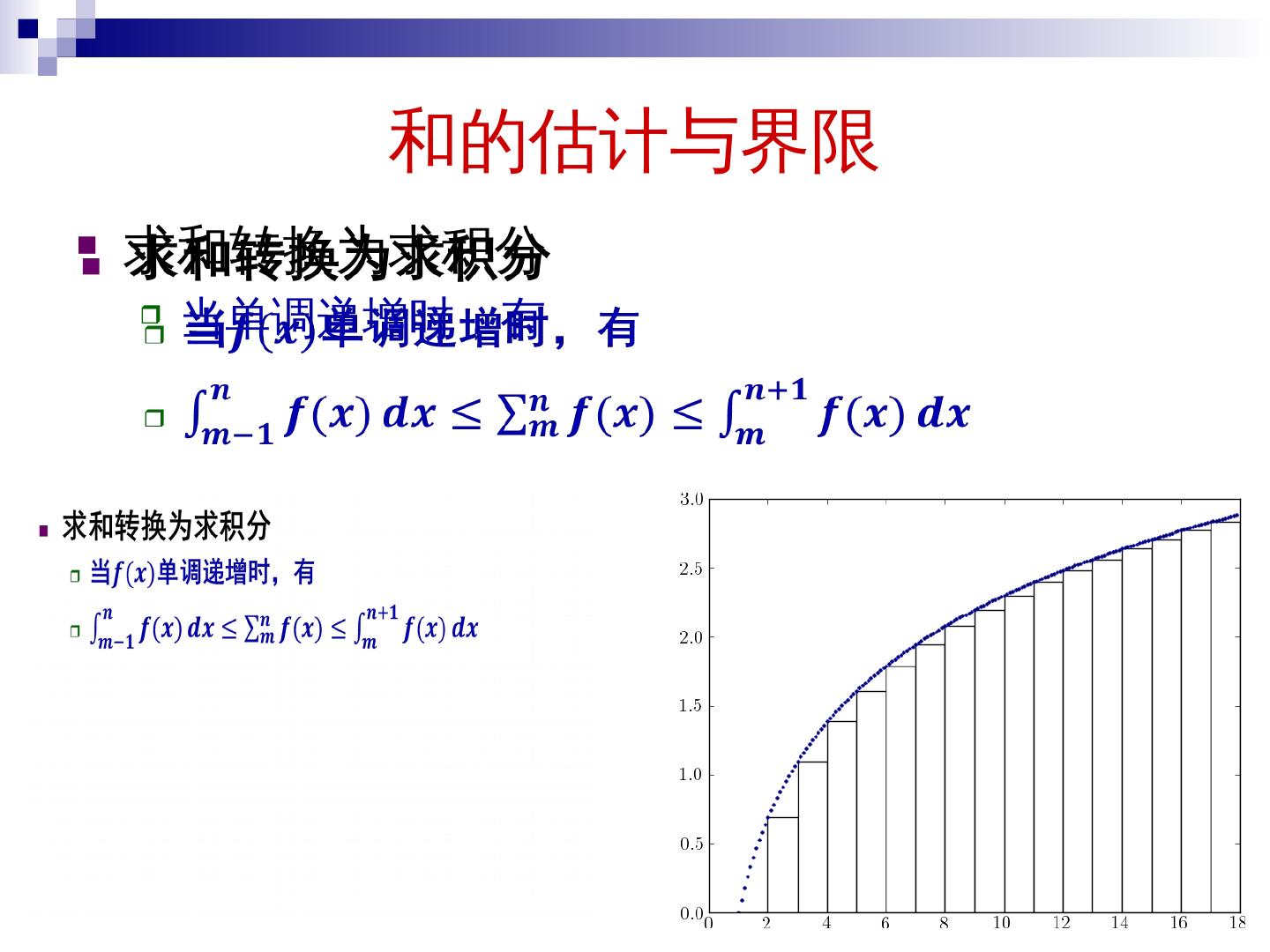
8 .和的估计与界限 直接求和的界限 8
9 .和的估计与界限 直接求和的界限 9
10 .和的估计与界限 直接求和的界限 对于所有 ,有 ,求 上界 … 10
11 .和的估计与界限 直接求和的界限 对于所有 ,有 ,求 上界 求 上界 11
12 .和的估计与界限 直接求和的界限 对于所有 ,有 ,求 上界 求 上界 当 时,有 12
13 .和的估计与界限 求和转换为求积分 曲线 之下面积 ∴ ∵ ∴ 13
14 .和的估计与界限 求和转换为求积分 曲线之下面积 ∵ ∴ 14
15 .和的估计与界限 求和转换为求积分 当 单调递增时,有 15
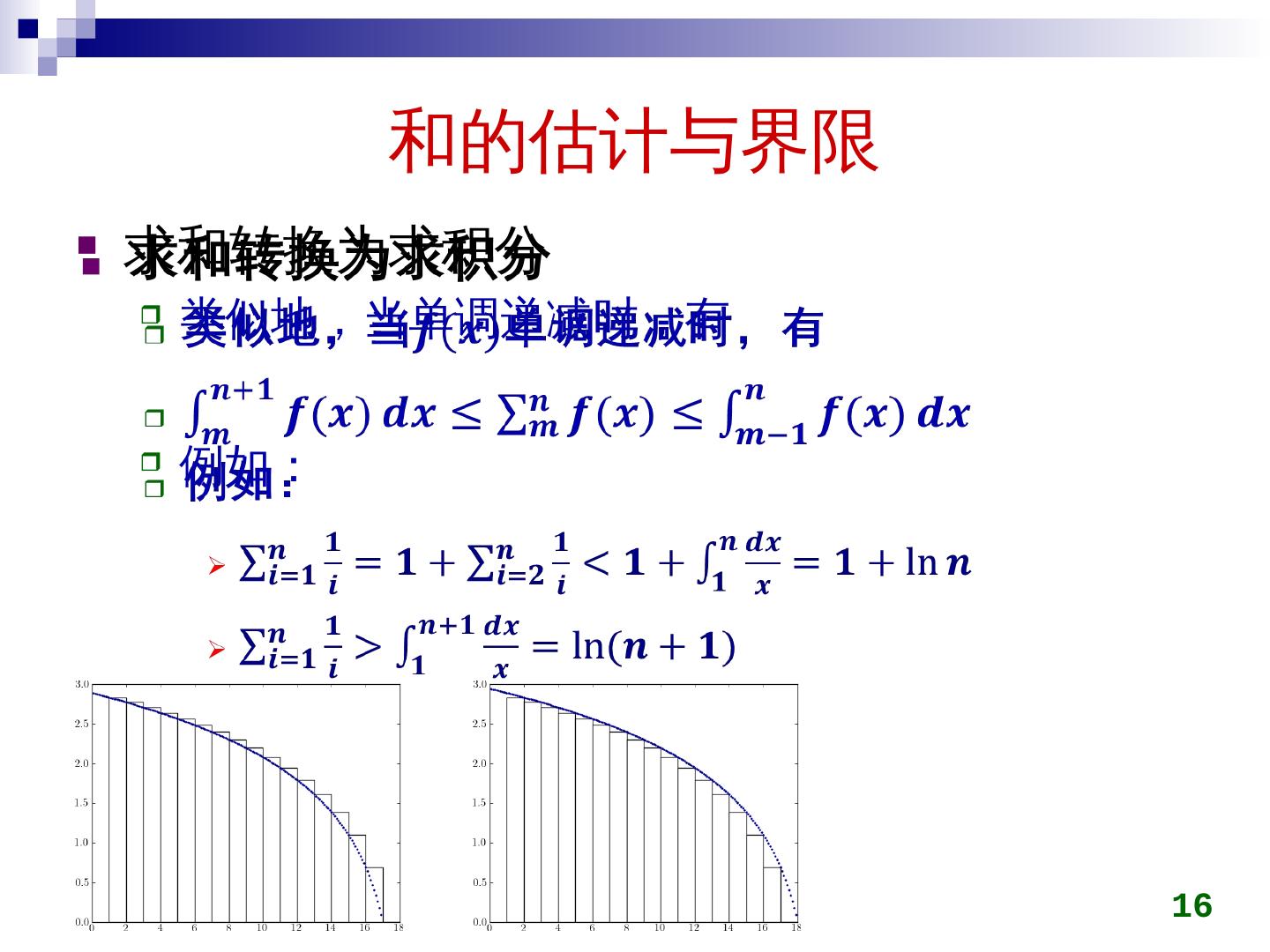
16 .和的估计与界限 求和转换为求积分 类似地,当 单调递减时,有 例如: 16
17 .递归方程 例: Merge-sort 排序算法的复杂性 方程 17
18 .递归方程 递归逐层展开求解 深度 ,最底层有 个 18
19 .递归方程 变量替换法求解 令 ,则 , 令 ,则 于是 显然 则 19
20 .递归方程 Master 定理求解 求解 型递归方程,其中 , 是常数, 是正函数 记住三种情况,可快速求解 20
21 .递归方程 Master 定理求解 求解 型递归方程,其中 , 是常数, 是正函数 若 , 是常数,则有 若 , 是常数 , 则 有 若 , 是常数 ,且对所有充分大的 有 , 是常数,则 有 21
22 .递归方程 Master 定理(直观理解,一般情况) 用 与 的阶比较, 若 更大,则 若 ,即 与 同阶, 则 有 若 更大,则 22 对于红色部分, Master 定理无能为力
23 .递归方程 Master 定理(更进一步理解) 用 与 的阶比较, 第一种情况, 不仅小于 ,而且要小于 ,即 第三种情况 , 不仅大 于 , 而且要大于 ,即 23 对于红色部分, Master 定理无能为力
24 .递归方程 Master 定理 (例子) 求解 , , , ∵ , 即 ∴ 24
25 .递归方程 Master 定理 (例子) 求解 , , , ∵ , ∴ 25
26 .递归方程 Master 定理 (例子) 求解 , , , ∵ , 对所有 n 有 ∴ 26
27 .递归方程 Master 定理 (例子) 求解 , , , 虽然 , 但是 渐近小于 27 落于此区域
28 .Master 定理证明 证明思路 对 展开可得 , 令 28
29 .Master 定理证明 证明思路 若 , 是常数,则有 ∴ 29