概率论与数理统计第十章---点估计

1 . 第十章 点估计  估计问题  估计方法  点估计的优良 性 

2 . 第十章 点估计 在实际问题中，经常遇到随机变量 X （即总体即总体 X ）的分布的分布 函数的形式已知，但它的一个或者多个参数未知的情形， 此时写不出确切的概率密度函数 . 若通过简单随机抽样，得 到总体 X 的一个样本观测值，我们自然会想到利用这一组数 据来估计这一个或多个未知参数 . 诸如此类，利用样本去估 计总体未知参数的问题，称为参数估计问题 . 参数估计问题有两类，分别是点估计和区间估计 . 而参 数估计是统计推断的一个重要组成部分，可以这样说统计 推断的基本问题可以分为两大类 : 一是参数估计问题， 二 是假设检验问题。 

3 . 数理统计问题：如何选取样本来对总体的种种统计 特征作出判断。 参数估计问题：知道随机变量（总体）的分布类型， 但确切的形式不知道，根据样本来估计总体的参数，这 类问题称为参数估计（ paramentric estimation ）。 参数估计的类型——点估计、区间估计 

4 . 第七章 点估计 参 点估计 估计未知参数的值 数 估  估计未知参数的取值范围， 计 区间估计 并使此范围包含未知参数的 真值的概率为给定的值 

5 . 第一节 点估计问题 　设总体 X 的分布函数 F （ x ， θ ）是已知的 ， θ 是未知的 分布参数，参数 θ 的所有可能取值组成的集合称为参数空间， 常用 Θ 表示，参数估计问题就是根据样本对上述未知参数做出 估计。当 X 为离散时， F （ x ， θ ）为分布律；当 X 为连续时 ， F （ x ， θ ）为密度函数． 　　设 X 1 , X 2 , , X n 是来自总体Ｘ 的一个样本，所谓统计模 X 1 , X 2 , , X n 型，即样本　　　　　的联合分布。由于样本是独立同分布 的．故可一般地表述统计模型为： F ( x1 ; )  F ( xn ; )    

6 . 第一节 点估计问题 例１　某种同型号产品Ｎ个，其合格率Ｎ个，其合格率个，其合格率 θ 未知，对该批 产品Ｎ个，其合格率作质量检验，从中随机抽取ｎ件（ｎ件（即总体ｎ件（ｎ << Ｎ个，其合格率）的分布．当 第ｉ次抽到的产品为合格时，记Ｘ次抽到的产品Ｎ个，其合格率为合格时，记ＸＸｉ次抽到的产品为合格时，记Ｘ＝１，反之记ＸＸｉ次抽到的产品为合格时，记Ｘ＝  i 1,, n  ０　　　　　．则　　　　　就是样本．总体分布为二 X 1 , X 2 ,, X n B 1,   点分布　　　，参数空间　　　　，容易得到统计模型   0,1 n  xi n  i1 1     ,    0,1 n xi i 1 例２　一批灯管寿命服从指数分布 E(λ), λ>0 未知，从 中随机抽取 n 支， X 1 , X 2 , , X n 为其寿命，则统计模型 n 为  xi  en i 1 ,    0,  其中 x1 , x2 ,, xn 只取大于 0 的实数值 

7 . 第一节 点估计问题 在统计模型 (1) 中，若知道 θ ，就完全知道了总体的分 布，因此在模型 (1) 下，统计推断的对象或者说各种统计 推断问题都是同这个未知参数 θ 有关。 假设模型 (1) 及有一个同 θ 有关的指标 η ， η=g(g(θ) , η 可以是向量值。我们的问题是：基于样本 X 1 , X 2 ,, X n ， 估计 g(θ) 。 注意： 虽然 g(·) 已知的函数，但 θ 未知，因而函数值 g(θ) 是未知的 

8 . 第一节 点估计问题 例 3 ：对某地区中学生做身高调查，假定身高 X 服 从正态分布 N(μ,σ2), 其 μ ,σ2 中均未知，调查目的是 为了了解该地区中学生的平均身高 . 今从中抽取 n 个人。测得其身高X 1 , X 2 , , X n ，由此估计 X , X ,  , X 平均身高 μ, 该问题的模型是 : n  1   1  n   exp  2   X i     ,   2  2    2 i 1  其中参数 θ(μ,σ2), 参数空间    ,  2   R,  2  0 ，估    计对象是 θ 中的一个分量 μ ，令 g (θ )= μ ，是一个定义在 Θ 上的已知函数，问题是：基于 X 1 , X 2 ,  , X ，由此估n 计未知函数值 g(θ) . 

9 . 第一节 点估计问题 例 4( 续例 3) 要在该地区中学生中挑选生排球队员 , 标准是其身高必须高于 1.90m. 问题是估计中选率 η. 由正态分布性质 , 可将 η 表示成如下的的已知函 数形式 :  1.90     P X  1.90 1       其中     是标准正态分布函数 , 这个函数在未知参 数    ,  2 处的值 η 正是要估计的对象 . 

10 . 第一节 点估计问题 点估计的思想方法： 　　设总体Ｘ的分布函数的形式已知，但含有一或多个未 知参数：　　　　　。设　　　　　　为总体的一个样 1 ,  2 ,,  k X 1 , X 2 ,, X n 本，构造ｋ个统计量ｋ个统计量个统计量 1  X 1 , X 2 , X n    2  X 1 , X 2 , X n    　随机变量     k  X 1 , X 2 , X n   

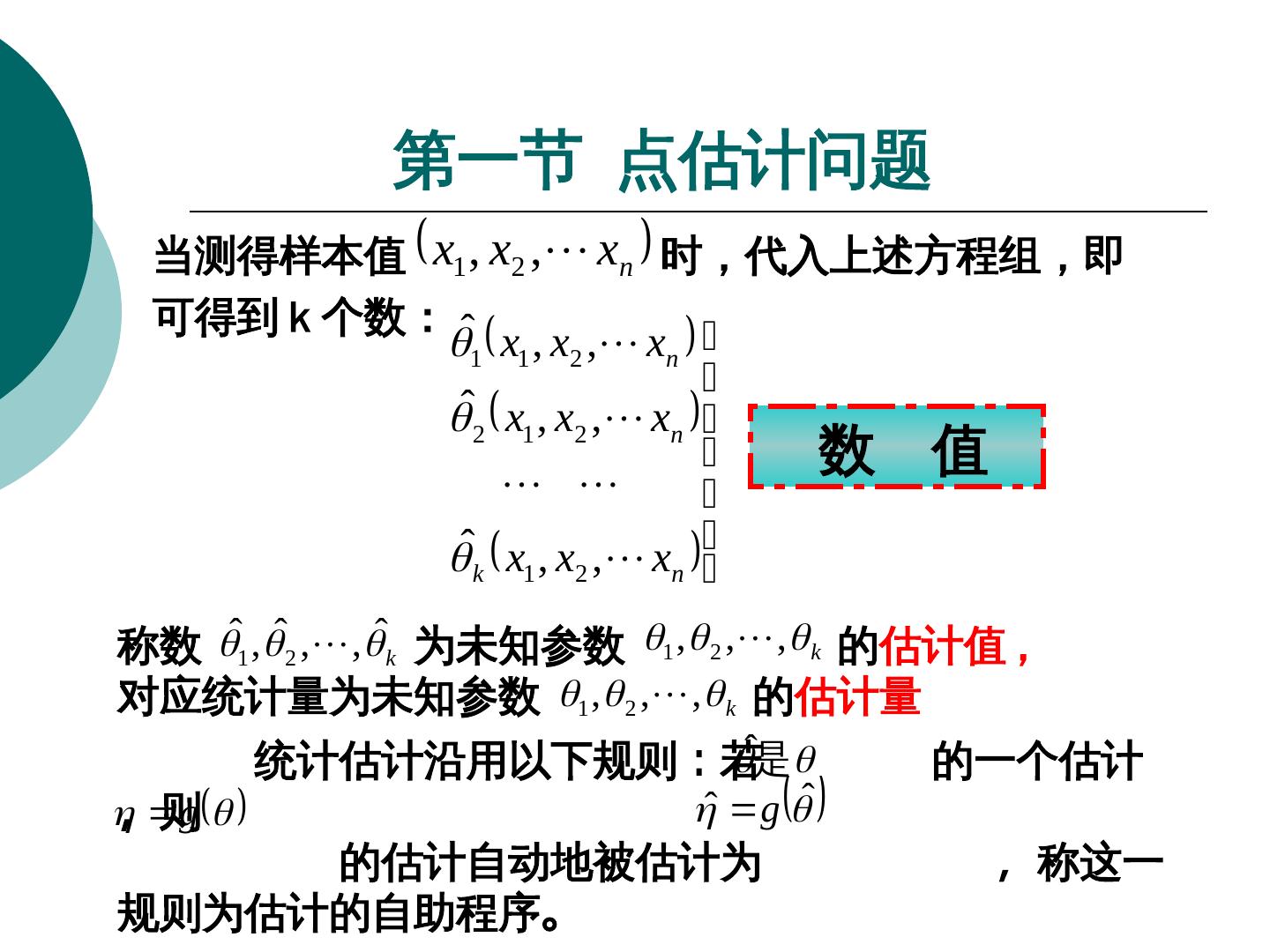
11 . 　　　第一节 点估计问题  x1 , x2 , xn  当测得样本值　　　　　　时，代入上述方程组，即 可得到ｋ个数：ｋ个数：个数： ˆ 1  x1 , x2 ,  xn    ˆ2  x1 , x2 ,  xn    　数　值      k  x1 , x2 ,  xn   ˆ ˆ1 , ˆ2 , , ˆk 称数　　　　　为未知参数　　　　　的估计值 1 ,  2 , ,  k , 对应统计量为未知参数　　　　　的估计量　 1 , 2 ,  , k 统计估计沿用以下规则：若 ˆ是 的一个估计  g   ，则 ˆ  g ˆ  的估计自动地被估计为 ，称这一 规则为估计的自助程序。 

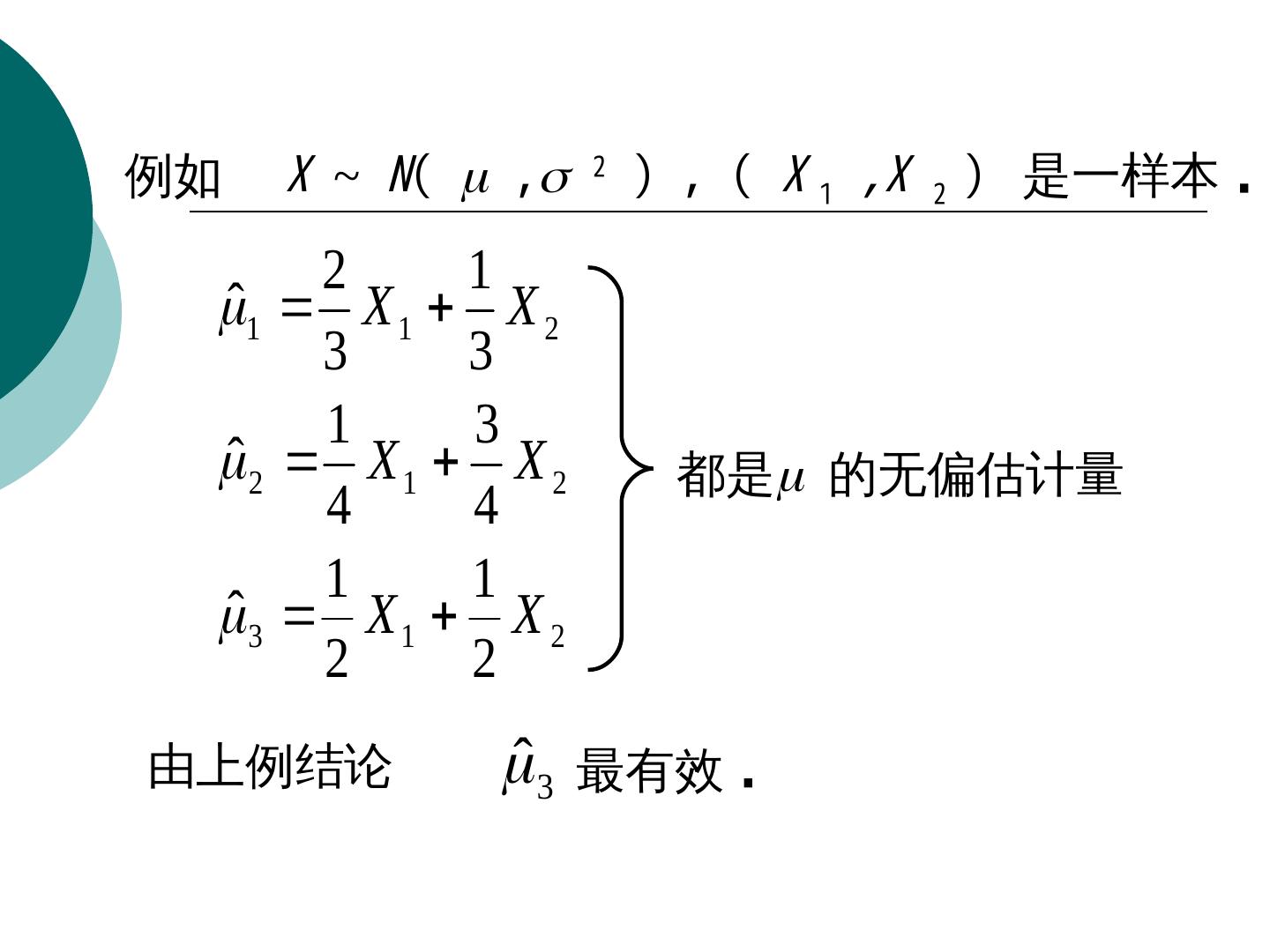
12 . 第一节 点估计问题 例如在例 4 中  1.90     P X  1.90 1       μ 的估计为 X ,σ 的估计为 S , 则 η 的估计是  1.90  X   P  X  1.90 1    说明 :  S  1. 给出 , 等同于给出 θ 的一种估计规则 ( 估计程 的估计量 ˆ . 序 ), 有了观 察数据 , 如何算出估计值 2. 估计量不必唯一 , 同一参数可以构造ｋ个统计量不同的统计量用以估计 . 因此有一个估计量好环的比较——评价估计量好环的准则 . 

13 . 第二节　估计方法 两种常用的构造ｋ个统计量估计量的方法： 矩估计法 极大似然估计法 一 . 矩估计法 • 定义：用样本矩来代替总体矩 , 从而得到总体分布 中参数的一种估计 . 这种估计方法称为矩估计法 . 它的思想实质是用样本的经验分布和样本矩去替换 总体的分布和总体矩 . 也称之为替换原则 . • 特点：不需要假定总体分布有明确的分布类型。 

14 . 第二节　估计方法 设总体 X 具有已知类型的概率函数 f(x;θ),θ),θ=g((θ1,…,θk)∈Θ 是 k 个未知参数 .(X1,X2,…,Xn) 是来自总体 X 的一个样本 . 假 若 X 的 k 阶矩 μk=g(E(Xk) 存在 , 则对于 i≤k, E(Xi) 都存在 , 并且  E ( X ) 1 (1 ,  2 ,..., k ) m1 是 (θ1,…,θk) 的函数 2 µi(θ1,…,θk).  E ( X )  2 (1 ,  2 ,..., k ) m2 1 n 设   ............................... mi   x n j 1 j i  E ( X k )  ( ,  ,..., ) m  k 1 2 k k 得到含有未知参数 (θ1,…,θk) 的 k 个方程 . 解这 k 个联立方程 组就可以得到 (θ1,…,θk) 的一组解 : 

15 . 第二节　估计方法  ˆ 1 ˆ 1 ( X 1 , X 2 ,..., X n )   ˆ 2 ˆ 2 ( X 1 , X 2 ,..., X n )   ................................... ˆ ˆ ( X , X ,..., X )   k   k 1 2 n 用上面的解来估计参数 θi 就是矩估计法 . 

16 . 第二节　估计方法 例 : 设总体 X 服从泊松分布，参数 λ 未知， ( X 1 , X 2 ,, X n ) 是来自总体的一个样本，求参数 λ 的矩估计量 . 解：总体 X 的期望为 1 E ( X ) m1  1 n 从而得到方程    X i n i 1 所以 λ 的矩估计量为 n 1 ˆ   X i  X n i 1 

17 . 第二节　估计方法 例 5 设有一批同型号灯管 , 其寿命 ( 单位： h)) 服从参数为 λ 的指 数分布，今随机抽取其中的 11 只，测得其寿命数据如下： 110 ， 184 ， 145 ， 122 ， 165 ， 143 ， 78 ， 129 ， 62 ， 130 ， 168 用矩估计法估计 λ 值。 1 解：设 X 为灯管的寿命，则 1 E  X      X  ˆ 1 1 m1 ,即 X, λ 的矩估计 1 n 已知 n=g(11 ， X 的观察值为 x   xi 130.55 h , n i 1 ˆ 1 因而 λ 的估计值为：  0.0077 130.55 

18 . 第二节　估计方法 例 6 设总体 X 有均值 μ 和方差 2 ，今有 6 个随机样本 的观察数据为： -1.20,0.82,0.12,0.45,-0.85,-0.30 求 μ 和  的矩估计量 2 . 解 : 参数   ,  2  是二维的 . 因为  1 E ( X )     2  E ( X 2 )  D ( X )   E ( X )  2  2   2  ˆ  0.16  2  X m1   ˆ 0.50  n  1 X 2 m  2   2  n  i 1 i 2   ˆ X 6  ˆ 2  1 2 解得μ 和  的矩估计量分别为   i n i 1 X 2  X 2 

19 . 第二节　估计方法 例 7 设 X , X , , X n (θ1,θ2) 上均匀分布样本 , 是来自 1 2 θ1<θ2 未知 . 求 θ1,θ2 的矩估计 .  1   2      X 解 : 因为 E  X   1 2    2 2       2 D X  E  X 2    E  X     S2  2 1 2  12 解得 θ1,θ2 的矩估计为： ˆ1 X  3S2 ˆ2 X  3S2 

20 . 例 : 设某炸药厂一天中发生着火现象的次数 X 服从 参数为λ的泊松分布， λ未知，有以下样本 值；试估计参数 λ。 着火的次数k 0 1 2 3 4 5 6 发生k次着火天数n k 75 90 54 22 6 2 1  250 解： E  X   1 n m1   X i  X n i 1 令 X  , ˆ 1 则  x  (0 75  1 90    6 1) 1.22 250 

21 .练习 对容量为 n 的子样，求下列密度函数中参数 a 的 矩估计量。  2  2 (a  x), (0  x  a ) f ( x )  a  0, 其它 a 2 a 解 由于 EX  x  2 (a  x)dx  0 a 3 a 所以由矩法估计，得 X  3 n  3 X  3 解得 a  n i 1 Xi n   3 所以，参数 a 的矩估计量为 a  n i 1 Xi 

22 . 第二节　估计方法 二 . 极大似然估计法 特点：适用总体的分布类型已知的统计模型 极大似然估计法是求估计用的最多的方法，它最早 是由高斯在 1821 年提出，但一般将之归功于费舍尔 (R.A.Fish)er) ，因为费舍尔在 1922 年再次提出了这种 想法，并证明它的一些性质，从而使得极大似然法得 到了广泛的应用。 为了叙述极大似然原理的直观想法，先看一个例子。 

23 . 第二节　估计方法 例如 : 有两外形相同的箱子 , 各装 100 个球 一箱 99 个白球 1 个红球 一箱 1 个白球 99 个红球 现从两箱中任取一箱 , 并从箱中任取一球 , 结果所取得的球是白球 . 问 : 所取的球来自哪一箱？ 答 : 第一箱 . 思想方法：一次试验就出现的 事件有较大的概率 

24 . 参数的极大似然估计法 思想：设总体 X 的密度函数为 f(x,) ，为未知参数，则 样本（ X1,X2,…,Xn ）的联合密度函数为 n f ( x1 , x2 , , xn ,  )  f ( xi ,  ) i 1 n 令 L( )  f ( x1 , x2 , , xn ,  )  f ( xi ,  ) i 1 参数的估计量 ˆ，使得 样本（ X1,X2,…,Xn ）落在观测 值 ( x1 , x2 , , xn ) 的邻域内的概率 L() 达到最大，即 L( x1 , x2 , , xn , ˆ) max L( x1 , x2 ,, xn ,  ) 则称 ˆ 为参数的极大似然估计值。 

25 .似然函数 : 定义:设总体 X 的分布类型已知,但含有未知参数θ . (1)设离散型总体 X 的概率分布律为 p( x; ) ，则样本 ( X 1 , X 2 , , X n ) 的联合分布律 n p ( x1 ; ) p ( x 2 ; )  p ( x n ; )  p ( xi ; ) i 1 n 称为似然函数，并记Ｘ之为 L( ) L( x , x ,, x ; )  p( x ; ) . 1 2 n i 1 i (2) 设连续型总体 X 的概率密度函数为 f ( x; ) ，则样 本 ( X 1 , X 2 ,, X n ) 的联合概率密度函数 n f ( x1 ; ) f ( x 2 ; )  f ( x n ; )  f ( xi ; ) i 1 n 仍称为似然函数，并记Ｘ之为 L( ) L( x , x ,, x ; )  f ( x ; ) . 1 2 n i 1 i 

26 . 第二节　估计方法 定义:设总体的分布类型已知,但含有未知参数θ. (1)设 (X , X ,, X ) 为总体 X 的一个样本观察值，若似 1 2 n 然函数 L( ) 在 ˆ ˆ( x , x ,, x ) 处取到ｋ个数：最大值，则称 1 2 n ˆ( x1 , x2 ,  , xn ) 为θ的极大似然估计值. (2)设 ( X , X ,, X ) 为总体 X的一个样本,若ˆ( x , x ,, x ) 为θ 1 2 n 1 2 n 的极大似然估计值, 则称 ˆ( X , X ,, X ) 为参 数 θ的 1 2 n 极大似然估计量. 

27 . 参数的极大似然估计法 求解方法： n （ 1 ）构造似然函数 L( )  f ( x1 , x2 , , xn ,  )  f ( xi ,  ) n i 1 （ 2 ）取自然对数 ln L( x1 , x2 , , xn ,  )  ln f ( xi ,  ) i 1 d ln L （ 3 ）令 0 d 其解 ˆ 即为参数的极大似然估计值。 若总体的密度函数中有多个参数 1 ， 2 ，…， n ，则将  ln L 第（ 3 ）步改为  0, (i 1, 2, , n) i 解方程组即可。 

28 .例 4 设X 是一随机变量，X 1 , X 2 ,...... X n 是它的一个样 本。    x  1 , 0  x  1,的极大似然估计量。 X 的分布密度如下，求参数 0     f  x;    0, 其它 n 解：似然函数（当 时）： 0  xi  1   L  时）：  n  xi  1 n i 1 ln L    n ln      1  ln xi i 1 d ln L    n n 由似然方程：    ln xi 0 d  i 1 n 1   n  ln x  ln xi i 1 1 参数  的极大似然估计量为ˆ  ln X 

29 . 第二节　估计方法 例 8 设X 1 , X 2 , , X n 是来自 N   ,   2 2 的样本，求 ,  极大似然估计  x  2 1  f X  x  解： X 的密度函数为： e 2 2 2    xi    2 n n 2 2 e 故似然函数为：L( )  f ( xi )  i 1 i 1 2  n n n 1  2    ( xi   )2 (2 ) ( ) e 2 2 2 2 i 1 所以对数似然函数为： n n n 1 2 2 2 ln L  ln(2 )  ln   2 2  i ( x i 1   ) 2