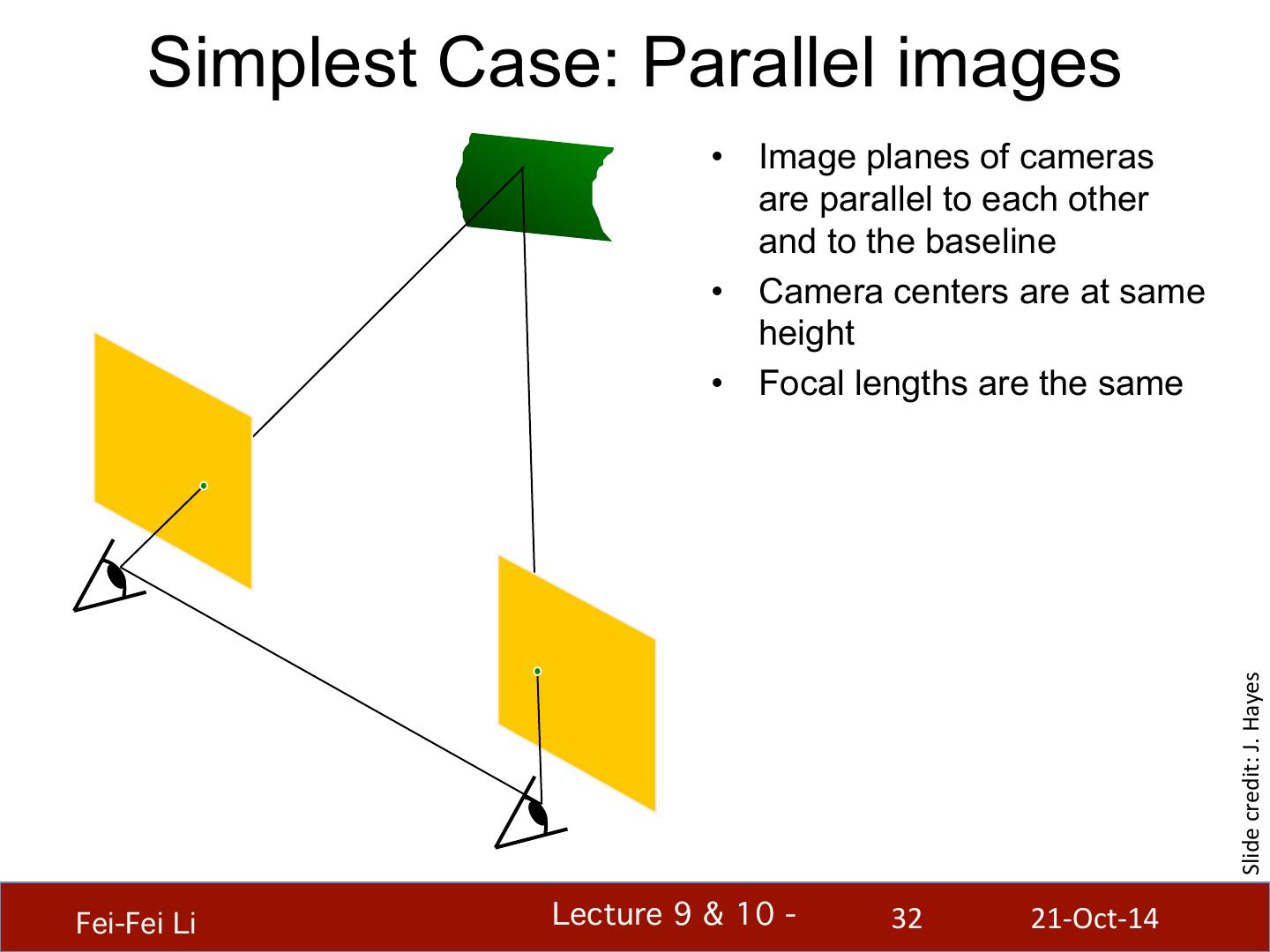
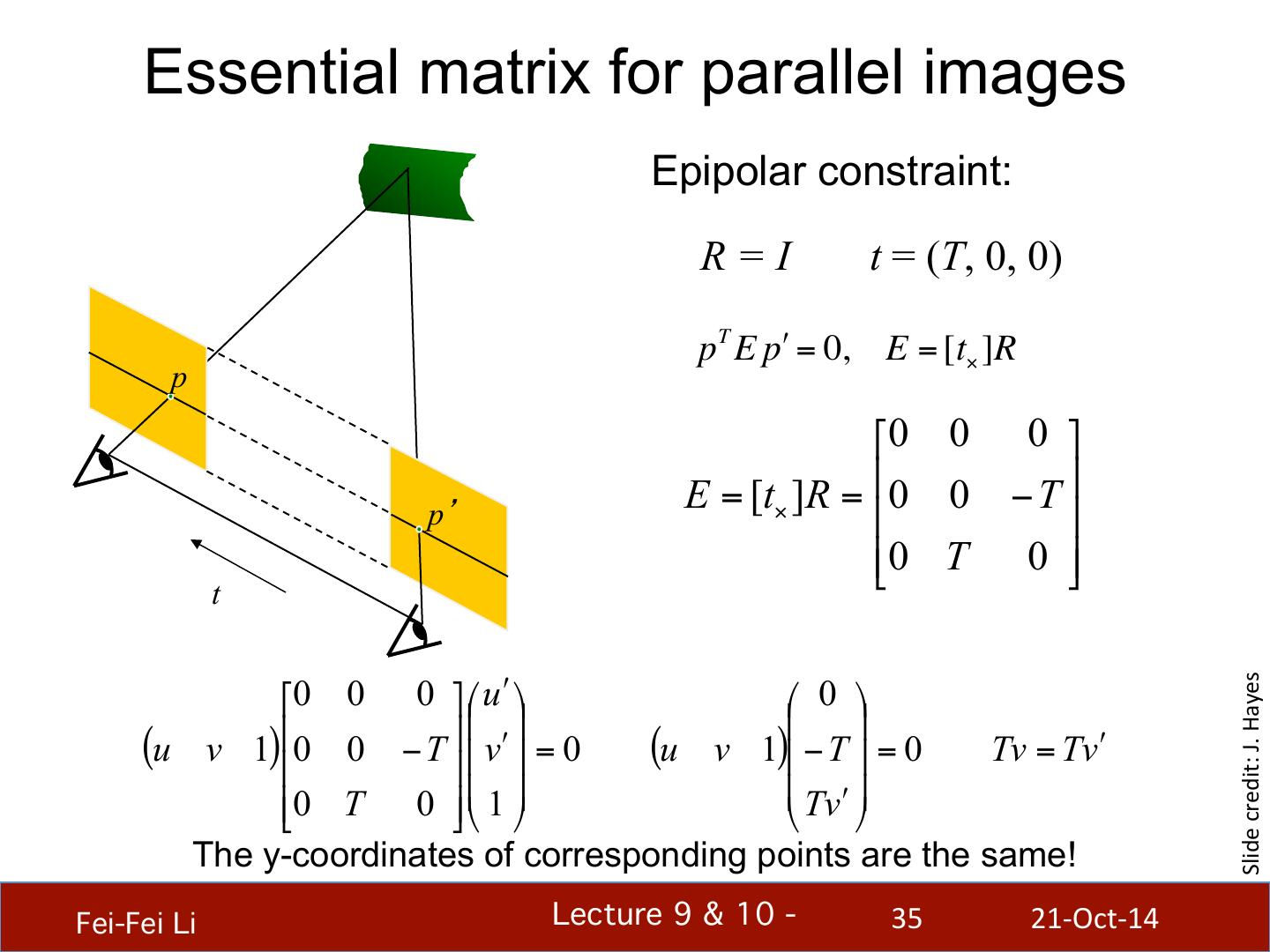
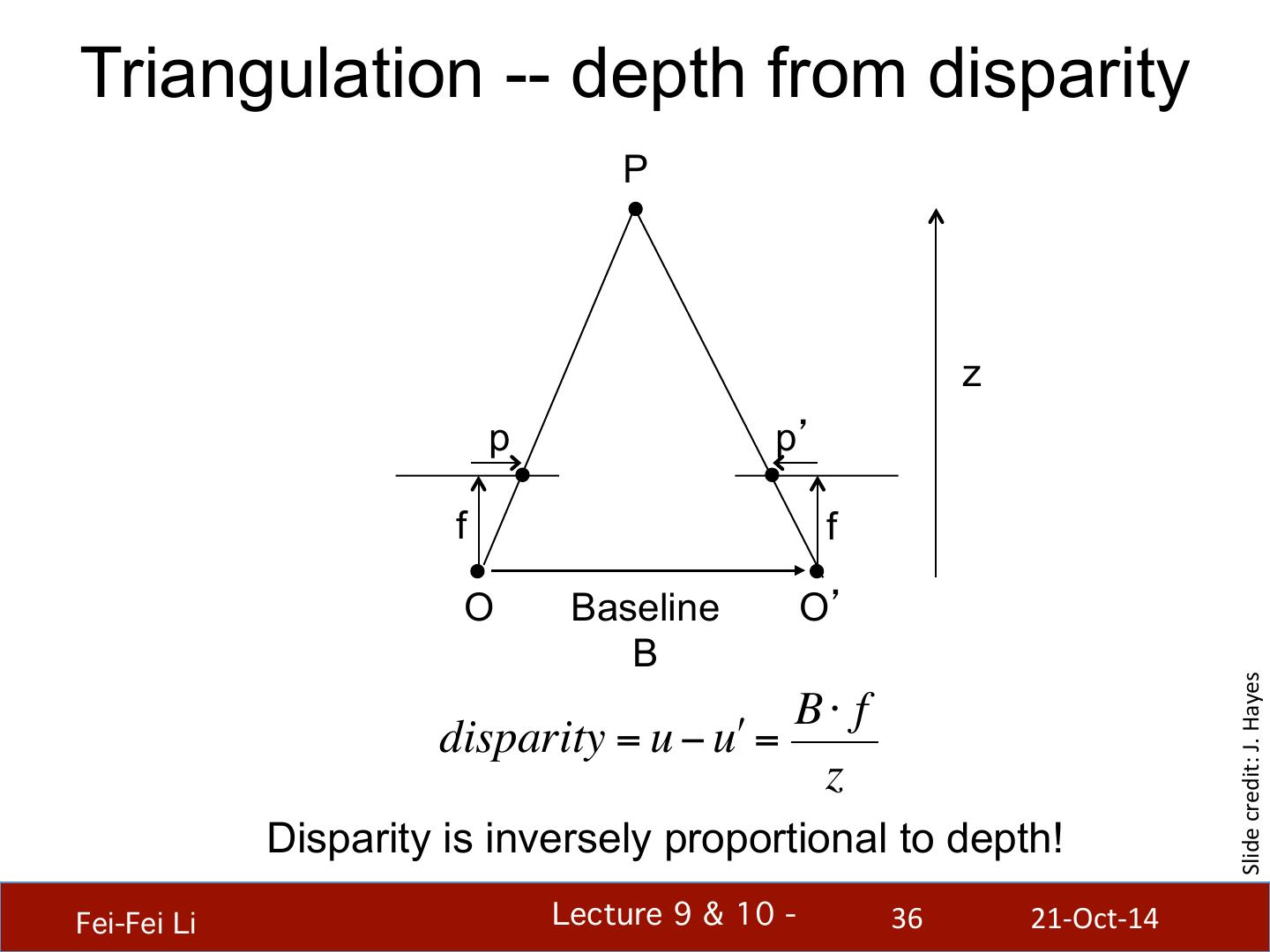
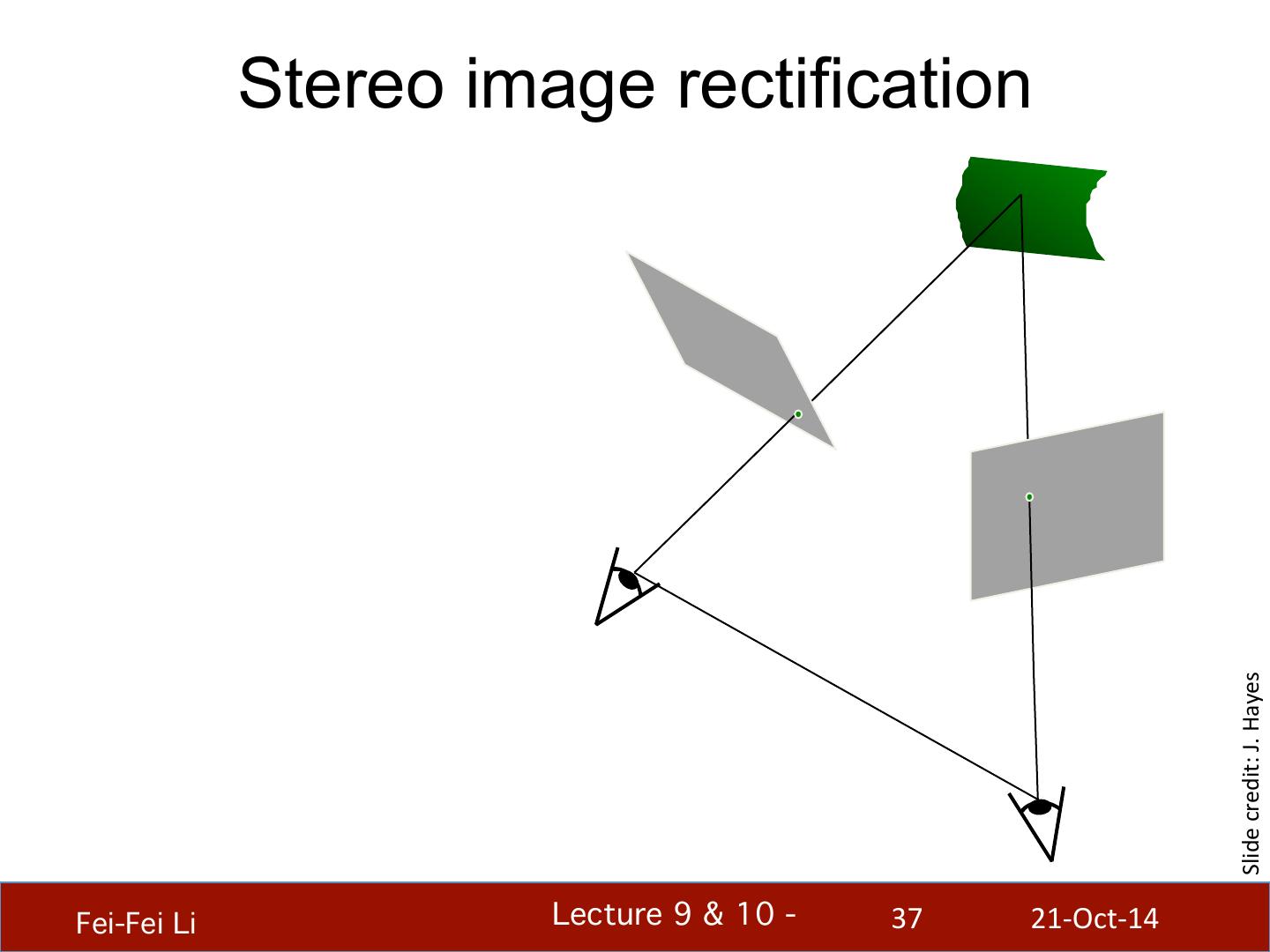
- 快召唤伙伴们来围观吧
- 微博 QQ QQ空间 贴吧
- 文档嵌入链接
- 复制
- 微信扫一扫分享
- 已成功复制到剪贴板
立体视觉
展开查看详情
1 . Lecture 9 & 10: Stereo Vision Professor Fei-‐Fei Li Stanford Vision Lab Fei-Fei Li! Lecture 9 & 10 - ! 1 21-‐Oct-‐14
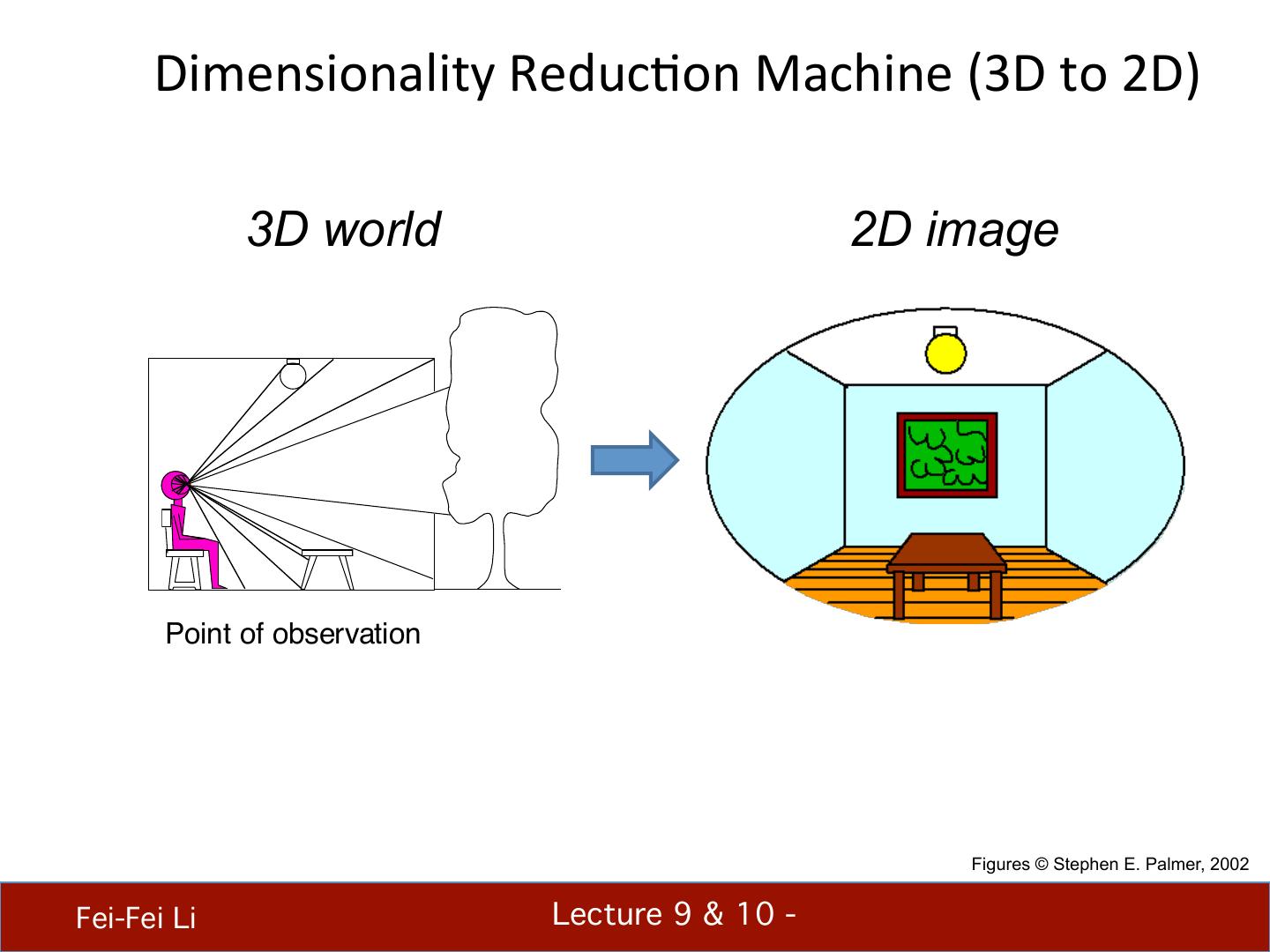
2 . Dimensionality ReducBon Machine (3D to 2D) 3D world 2D image Point of observation Figures © Stephen E. Palmer, 2002 Fei-Fei Li! Lecture 9 & 10 - !
3 . Pinhole camera f f ⎧ x ⎪⎪x ' = f z • Common to draw image plane in front of the focal ⎨ ⎪ y' = f y point ⎪⎩ z • Moving the image plane merely scales the image. Fei-Fei Li! Lecture 9 & 10 - ! 3 21-‐Oct-‐14
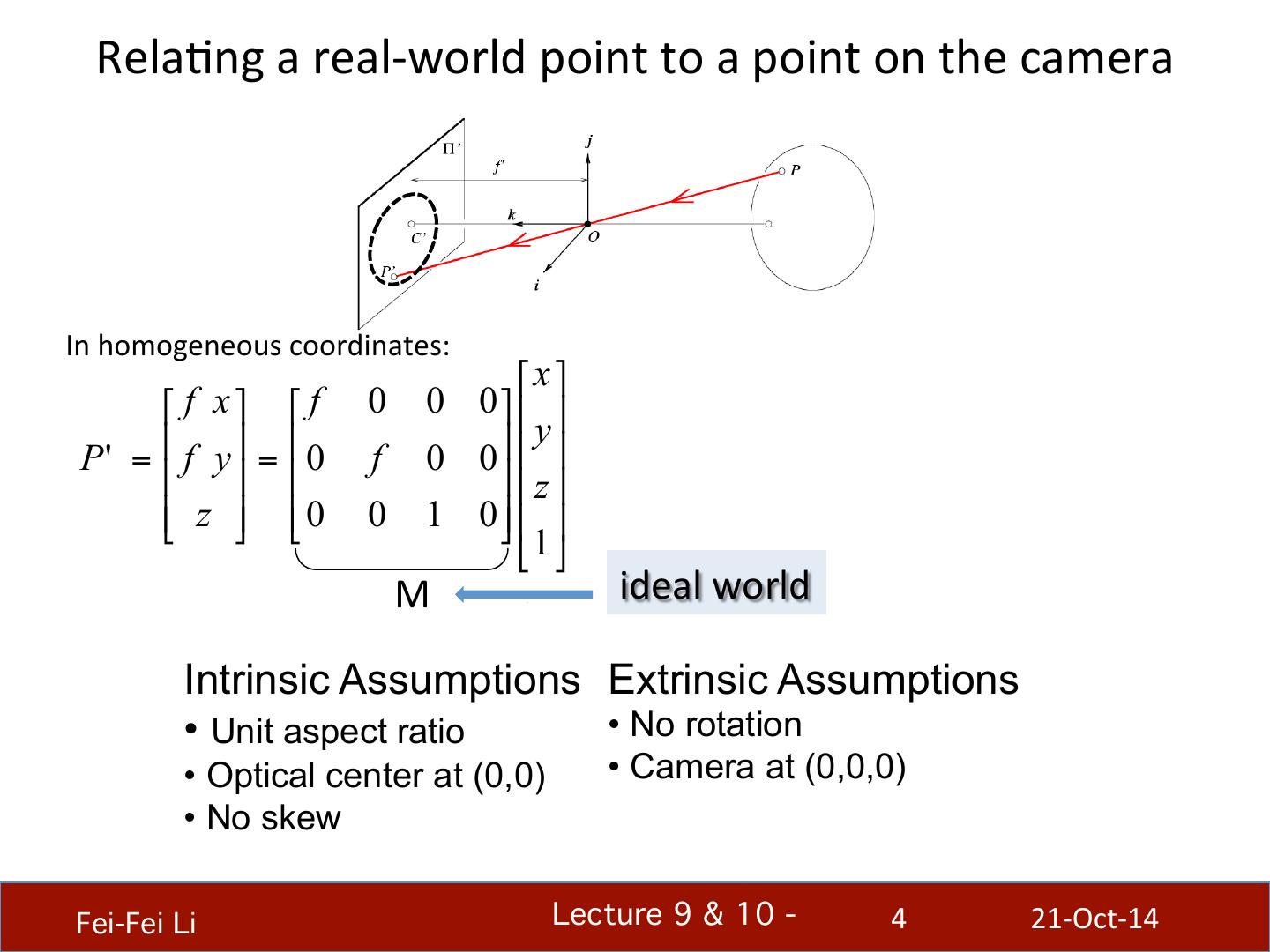
4 . RelaBng a real-‐world point to a point on the camera In homogeneous coordinates: ⎡ x ⎤ ⎡ f x ⎤ ⎡ f 0 0 0⎤ ⎢ ⎥ y ⎥ P' = ⎢⎢ f y ⎥⎥ = ⎢⎢ 0 f ⎥ 0 0⎥ ⎢ ⎢ z ⎥ ⎢⎣ z ⎥⎦ ⎢⎣ 0 0 1 0⎥⎦ ⎢ ⎥ ⎣ 1 ⎦ M ideal world Intrinsic Assumptions Extrinsic Assumptions • Unit aspect ratio • No rotation • Optical center at (0,0) • Camera at (0,0,0) • No skew Fei-Fei Li! Lecture 9 & 10 - ! 4 21-‐Oct-‐14
5 . RelaBng a real-‐world point to a point on the camera In homogeneous coordinates: ! f x $ ! f $! x $ 0 0 0 # & # & # & y & P' =# f y &=# 0 f 0 0 &# = K [I 0] P # & # &# z & #" z &% " 0 0 1 0 %# & 1 % " K Intrinsic Assumptions Extrinsic Assumptions • Unit aspect ratio • No rotation • Optical center at (0,0) • Camera at (0,0,0) • No skew Fei-Fei Li! Lecture 9 & 10 - ! 5 21-‐Oct-‐14
6 . Real-‐world camera Intrinsic Assumptions Extrinsic Assumptions • Optical center at (u0, v0) • No rotation • Rectangular pixels • Camera at (0,0,0) • Small skew Intrinsic parameters ⎡ x ⎤ ⎡u ⎤ ⎡α s u0 0⎤ ⎢ ⎥ ! # y P' = K" I 0 $P w ⎢ v ⎥ = ⎢ 0 β v0 ⎥ 0 ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ z ⎥ ⎢⎣1 ⎥⎦ ⎢⎣ 0 0 1 0⎥⎦ ⎢ ⎥ ⎣ 1 ⎦ Slide inspiraBon: S. Savarese Fei-Fei Li! Lecture 9 & 10 - !
7 . Real-‐world camera + Real-‐world transformaBon Intrinsic Assumptions Extrinsic Assumptions • Optical center at (u0, v0) • Allow rotation • Rectangular pixels • Camera at (tx,ty,tz) • Small skew ⎡ x ⎤ ⎡u ⎤ ⎡α s u0 ⎤ ⎡ r11 r12 r13 t x ⎤ ⎢ ⎥ y P ' = K [R t]P w ⎢ v ⎥ = ⎢ 0 β v0 ⎥ ⎢r21 r22 r23 ⎥ t y ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ z ⎥ ⎢⎣1 ⎥⎦ ⎢⎣ 0 0 1 ⎥⎦ ⎢⎣r31 r32 r33 t z ⎥⎦ ⎢ ⎥ ⎣ 1 ⎦ Slide inspiraBon: S. Savarese Fei-Fei Li! Lecture 9 & 10 - !
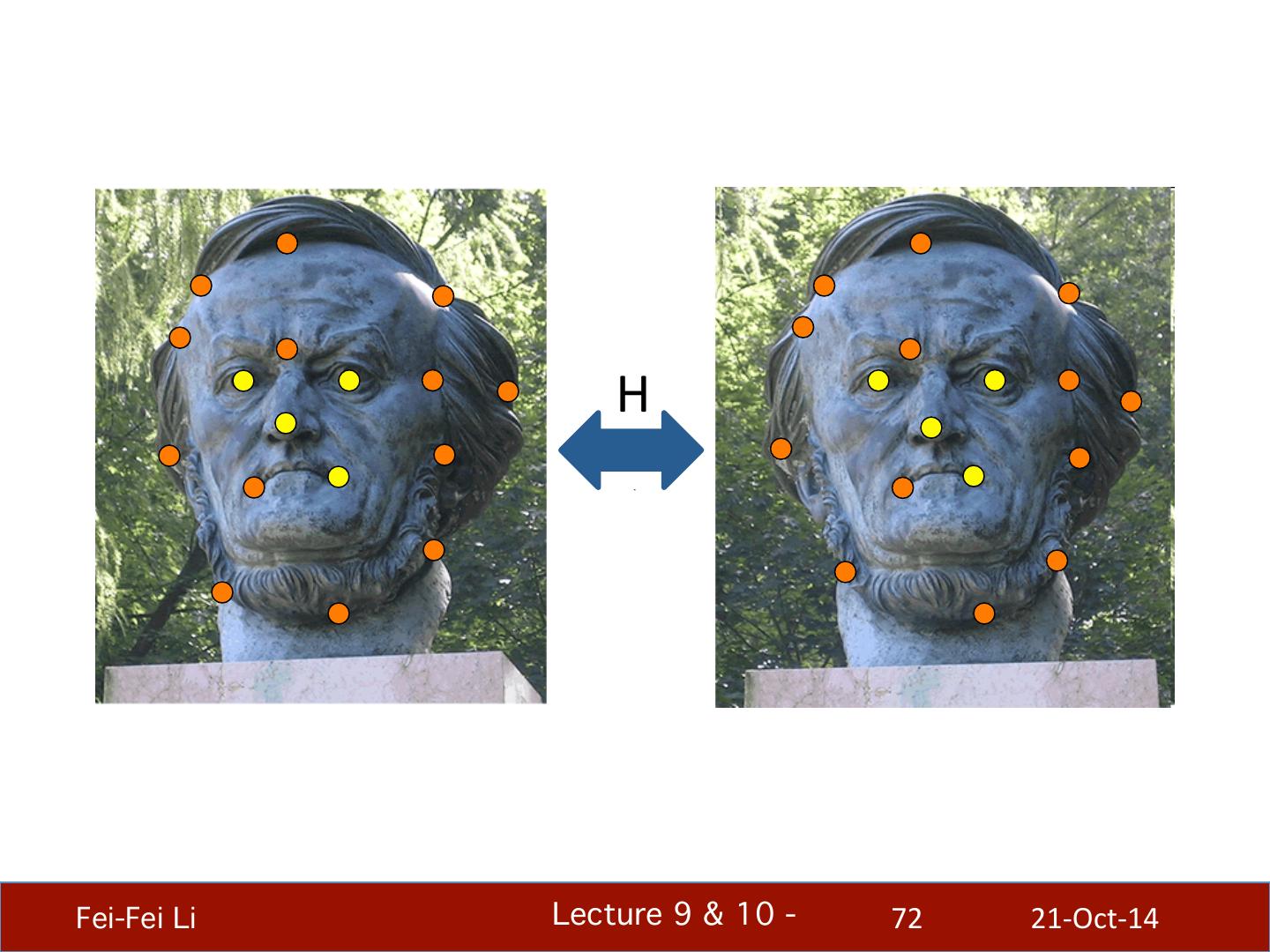
8 . What we will learn today? • IntroducBon to stereo vision • Epipolar geometry: a gentle intro • Parallel images & image recBficaBon • Solving the correspondence problem • Homographic transformaBon • AcBve stereo vision system Reading: [HZ] Chapters: 4, 9, 11 [FP] Chapters: 10 Fei-Fei Li! Lecture 9 & 10 - ! 8 21-‐Oct-‐14
9 . What we will learn today? • IntroducBon to stereo vision • Epipolar geometry: a gentle intro • Parallel images & image recBficaBon • Solving the correspondence problem • Homographic transformaBon • AcBve stereo vision system Reading: [HZ] Chapters: 4, 9, 11 [FP] Chapters: 10 Fei-Fei Li! Lecture 9 & 10 - ! 9 21-‐Oct-‐14
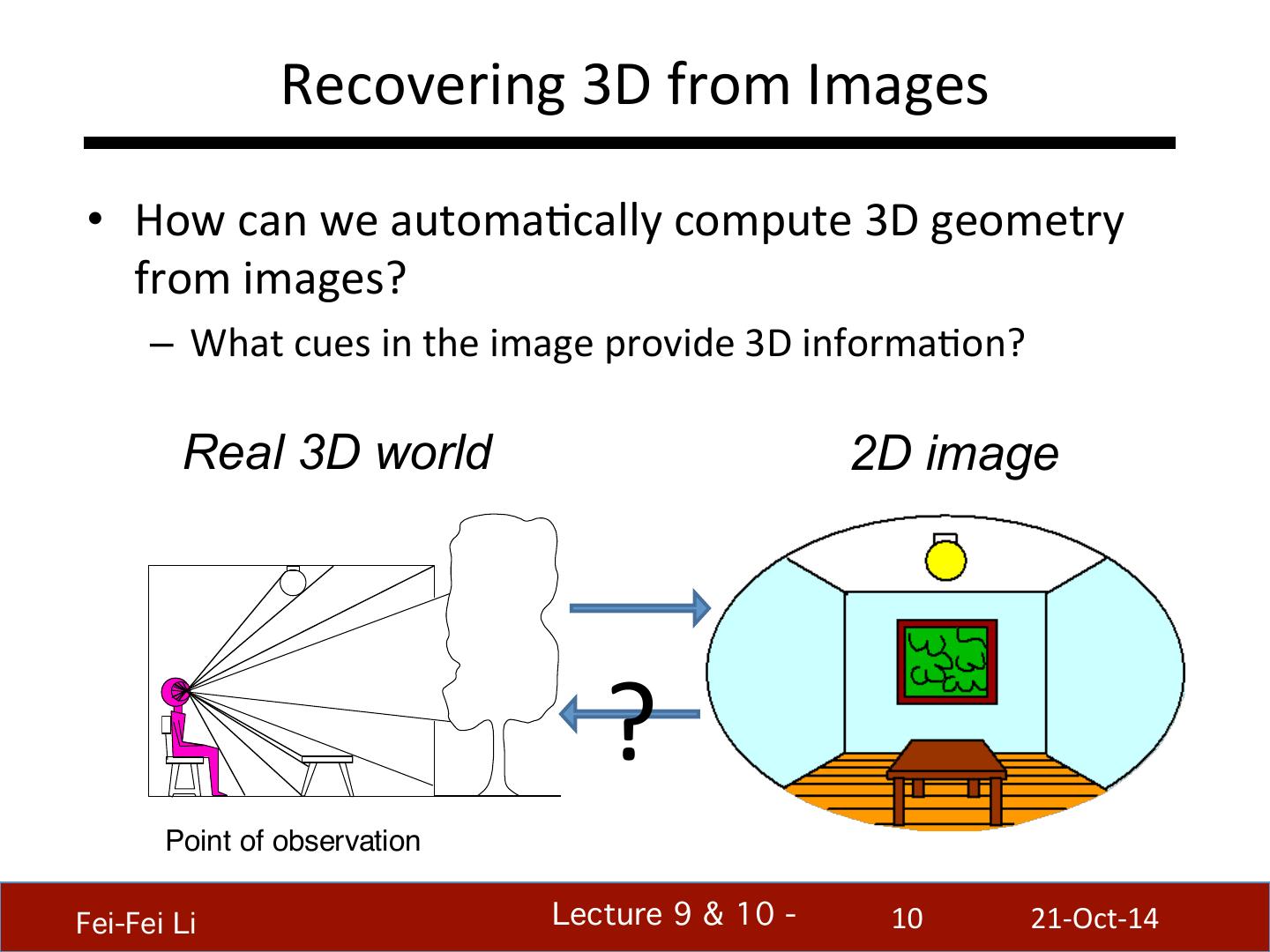
10 . Recovering 3D from Images • How can we automaBcally compute 3D geometry from images? – What cues in the image provide 3D informaBon? Real 3D world 2D image ? Point of observation Fei-Fei Li! Lecture 9 & 10 - ! 10 21-‐Oct-‐14
11 . Visual Cues for 3D • Shading Slide credit: J. Hayes Merle Norman Cosme5cs, Los Angeles Fei-Fei Li! Lecture 9 & 10 - ! 11 21-‐Oct-‐14
12 . Visual Cues for 3D • Shading • Texture Slide credit: J. Hayes The Visual Cliff, by William Vandivert, 1960 Fei-Fei Li! Lecture 9 & 10 - ! 12 21-‐Oct-‐14
13 . Visual Cues for 3D • Shading • Texture • Focus Slide credit: J. Hayes From The Art of Photography, Canon Fei-Fei Li! Lecture 9 & 10 - ! 13 21-‐Oct-‐14
14 . Visual Cues for 3D • Shading • Texture • Focus Slide credit: J. Hayes • MoBon Fei-Fei Li! Lecture 9 & 10 - ! 14 21-‐Oct-‐14
15 . Visual Cues for 3D • Others: • Shading – Highlights – Shadows – Silhoueaes • Texture – Inter-‐reflecBons – Symmetry – Light PolarizaBon • Focus – ... Slide credit: J. Hayes Shape From X • MoBon • X = shading, texture, focus, moBon, ... • We’ll focus on the moBon cue Fei-Fei Li! Lecture 9 & 10 - ! 15 21-‐Oct-‐14
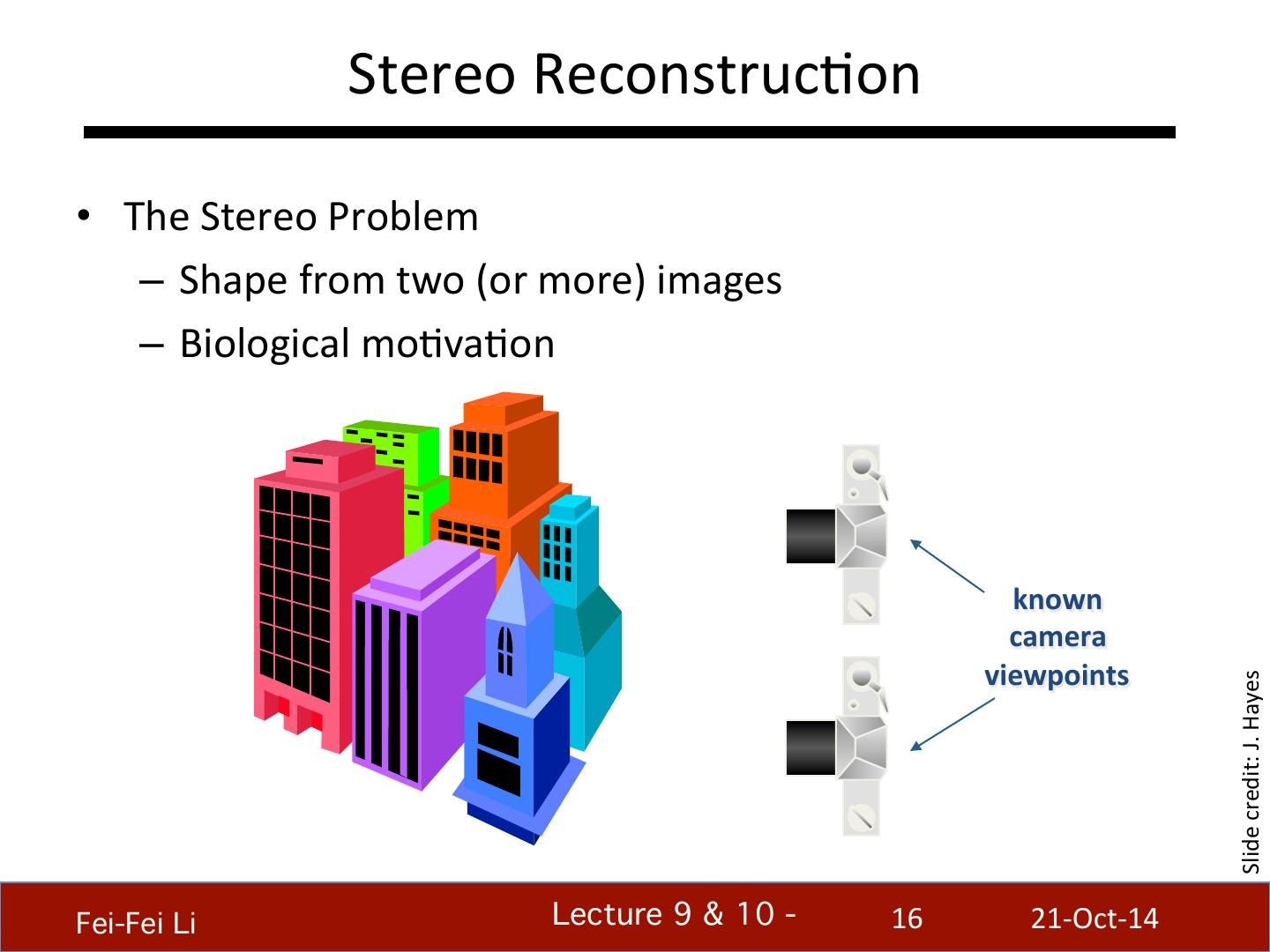
16 . Stereo ReconstrucBon • The Stereo Problem – Shape from two (or more) images – Biological moBvaBon known camera viewpoints Slide credit: J. Hayes Fei-Fei Li! Lecture 9 & 10 - ! 16 21-‐Oct-‐14
17 . Why do we have two eyes? Slide credit: J. Hayes Cyclope vs. Odysseus Fei-Fei Li! Lecture 9 & 10 - ! 17 21-‐Oct-‐14
18 . 1. Two is beaer than one Slide credit: J. Hayes Fei-Fei Li! Lecture 9 & 10 - ! 18 21-‐Oct-‐14
19 . 2. Depth from Convergence Slide credit: J. Hayes Human performance: up to 6-8 feet Fei-Fei Li! Lecture 9 & 10 - ! 19 21-‐Oct-‐14
20 . What we will learn today? • IntroducBon to stereo vision • Epipolar geometry: a gentle intro • Parallel images & image recBficaBon • Solving the correspondence problem • Homographic transformaBon • AcBve stereo vision system Reading: [HZ] Chapters: 4, 9, 11 [FP] Chapters: 10 Fei-Fei Li! Lecture 9 & 10 - ! 20 21-‐Oct-‐14
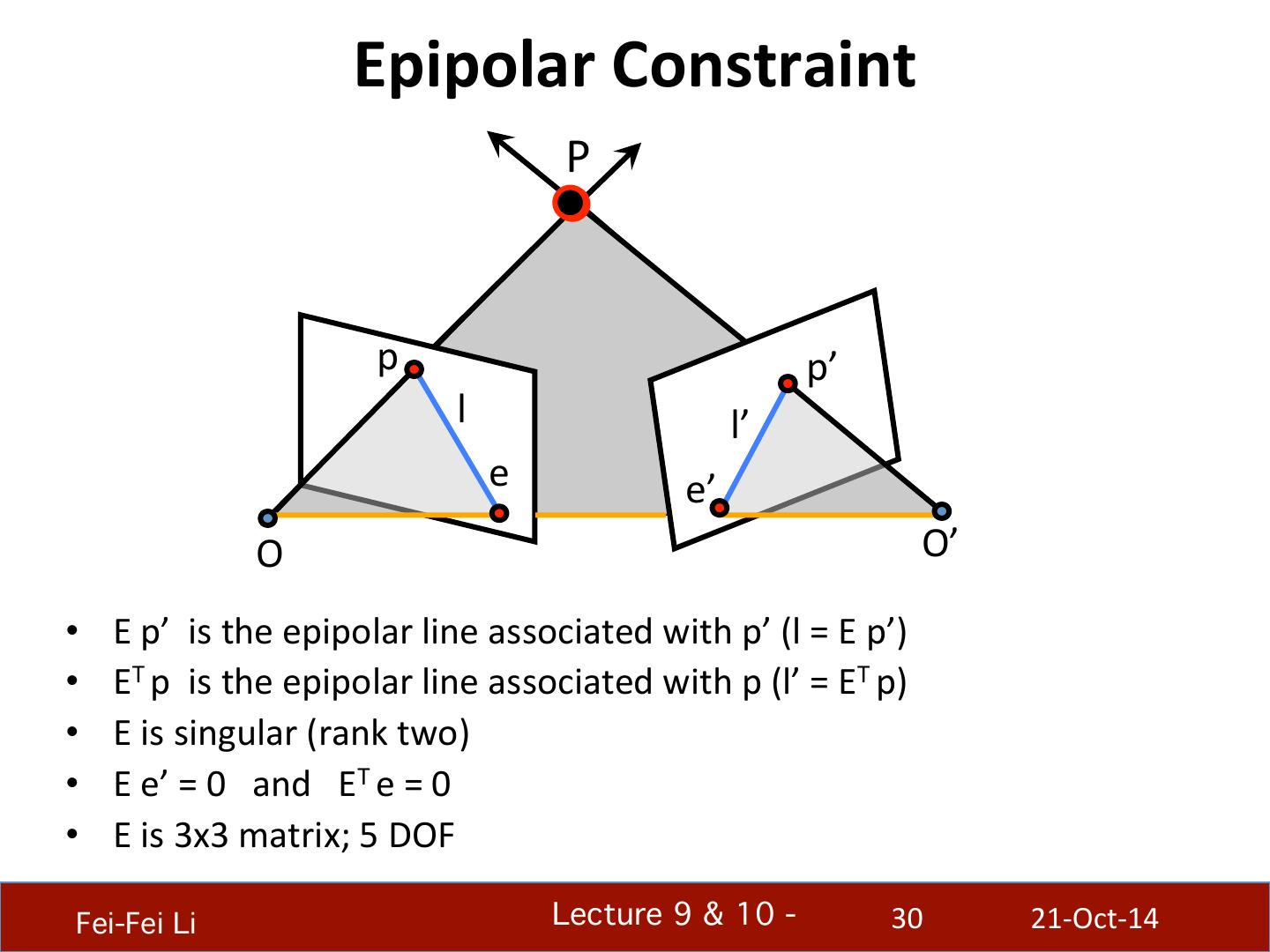
21 . Epipolar geometry P p p’ e e’ O O’ • Epipolar Plane • Epipoles e, e’ = intersecBons of baseline with image planes • Baseline = projecBons of the other camera center • Epipolar Lines = vanishing points of camera moBon direcBon Fei-Fei Li! Lecture 9 & 10 - ! 21 21-‐Oct-‐14
22 . Example: Converging image planes Fei-Fei Li! Lecture 9 & 10 - ! 22 21-‐Oct-‐14
23 . Epipolar Constraint -‐ Two views of the same object -‐ Suppose I know the camera posiBons and camera matrices -‐ Given a point on lem image, how can I find the corresponding point on right image? Fei-Fei Li! Lecture 9 & 10 - ! 23 21-‐Oct-‐14
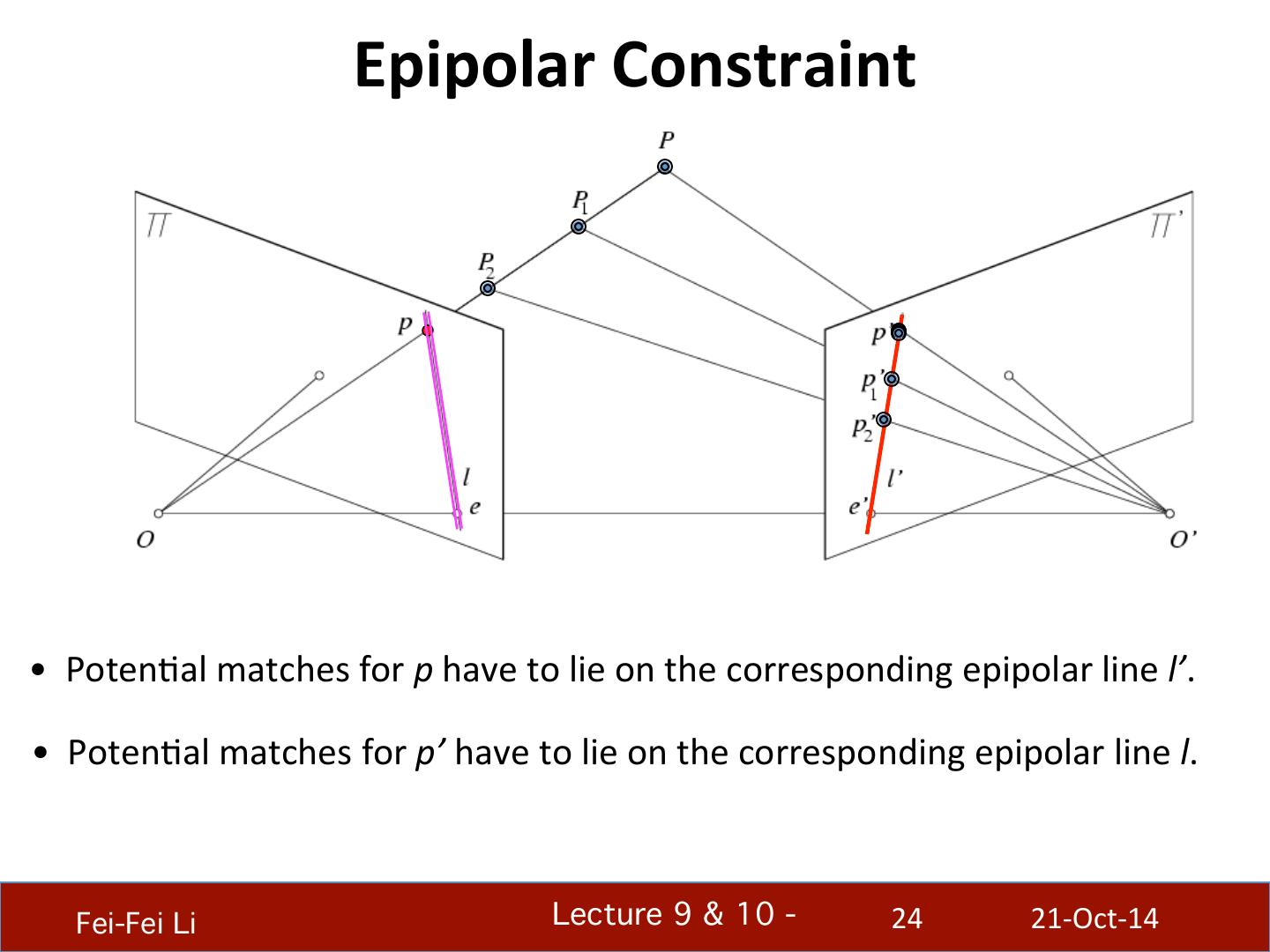
24 . Epipolar Constraint • PotenBal matches for p have to lie on the corresponding epipolar line l’. • PotenBal matches for p’ have to lie on the corresponding epipolar line l. Fei-Fei Li! Lecture 9 & 10 - ! 24 21-‐Oct-‐14
25 . Epipolar Constraint P ⎡u ⎤ ⎡u ʹ′⎤ p → M P = ⎢⎢ v ⎥⎥ p → M ʹ′ P = ⎢⎢ vʹ′ ⎥⎥ ⎢⎣1 ⎥⎦ ⎢⎣ 1 ⎥⎦ p p’ O O’ R, T M = K !" I 0 #$ M ' = K '!" R T #$ Fei-Fei Li! Lecture 9 & 10 - ! 25 21-‐Oct-‐14
26 . Epipolar Constraint P p’ p O R, T O’ M = K !" I 0 #$ K1 and K2 are known (calibrated cameras) M ' = K '!" R T #$ M = [I 0] M ' = [R T ] Fei-Fei Li! Lecture 9 & 10 - ! 26 21-‐Oct-‐14
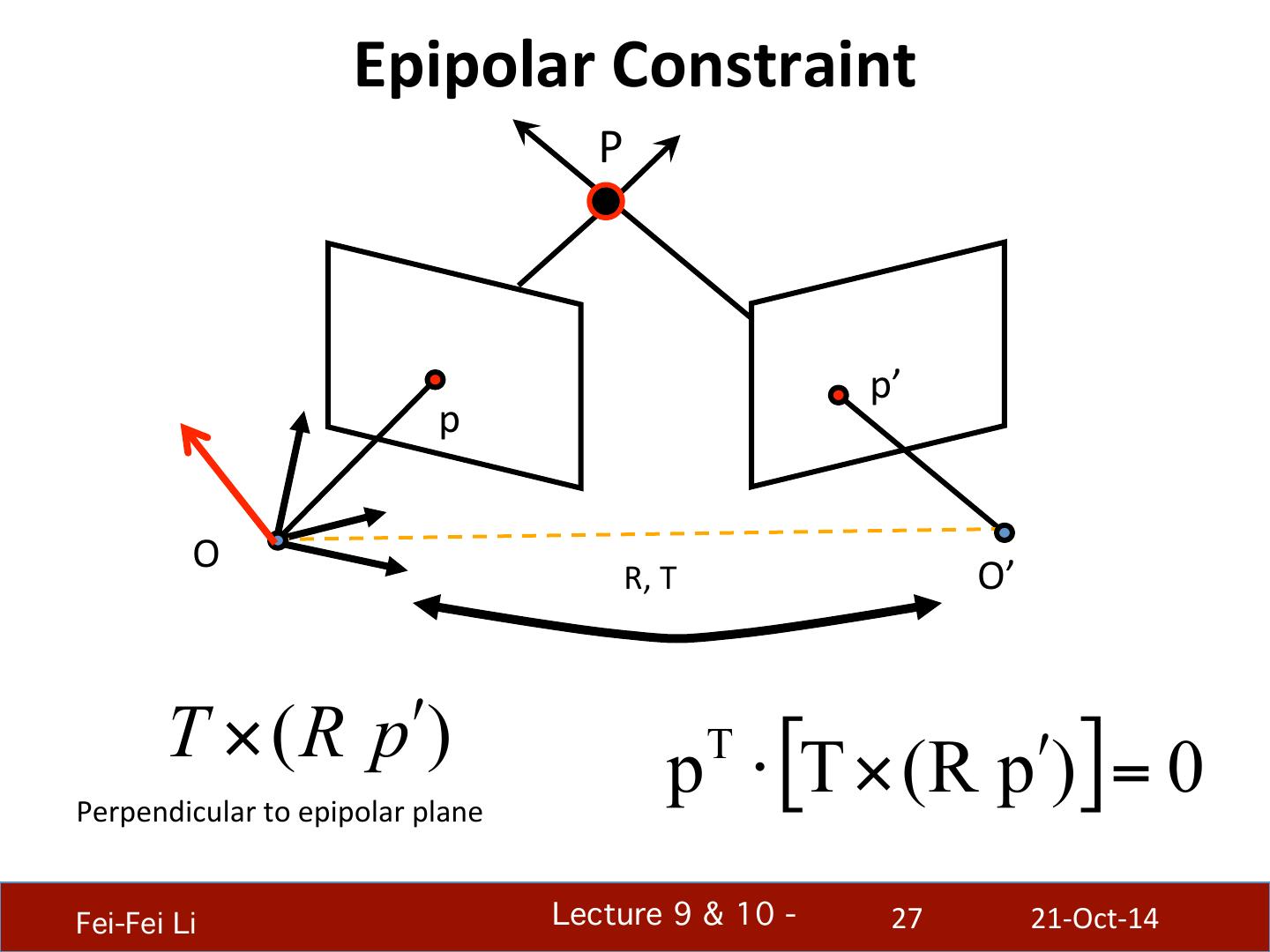
27 . Epipolar Constraint P p’ p O R, T O’ T × ( R pʹ′) T p ⋅ [T × (R pʹ′)] = 0 Perpendicular to epipolar plane Fei-Fei Li! Lecture 9 & 10 - ! 27 21-‐Oct-‐14
28 . Cross product as matrix mulBplicaBon ⎡ 0 − az a y ⎤ ⎡bx ⎤ ⎢ ⎥ ⎢ ⎥ a × b = ⎢ az 0 − ax ⎥ ⎢by ⎥ = [a× ]b ⎢− a y ax 0 ⎥⎦ ⎢⎣bz ⎥⎦ ⎣ “skew symmetric matrix” Fei-Fei Li! Lecture 9 & 10 - ! 28 21-‐Oct-‐14
29 . Epipolar Constraint P p’ p O R, T O’ T T p ⋅ [T × (R pʹ′)] = 0 → p ⋅ [T× ]⋅ R pʹ′ = 0 (Longuet-‐Higgins, 1981) E = essenBal matrix Fei-Fei Li! Lecture 9 & 10 - ! 29 21-‐Oct-‐14