展开查看详情
3 .集成学习 个体 与集成 Boosting Adaboost Bagging 与随机森林 结合策略 平均法 投票 法 学习 法 多样性 误差 - 分歧分解 多样性度量 多样性扰动
4 .个体与集成 集成学习 (ensemble learning) 通过构建并结合多个学习器来提升性能
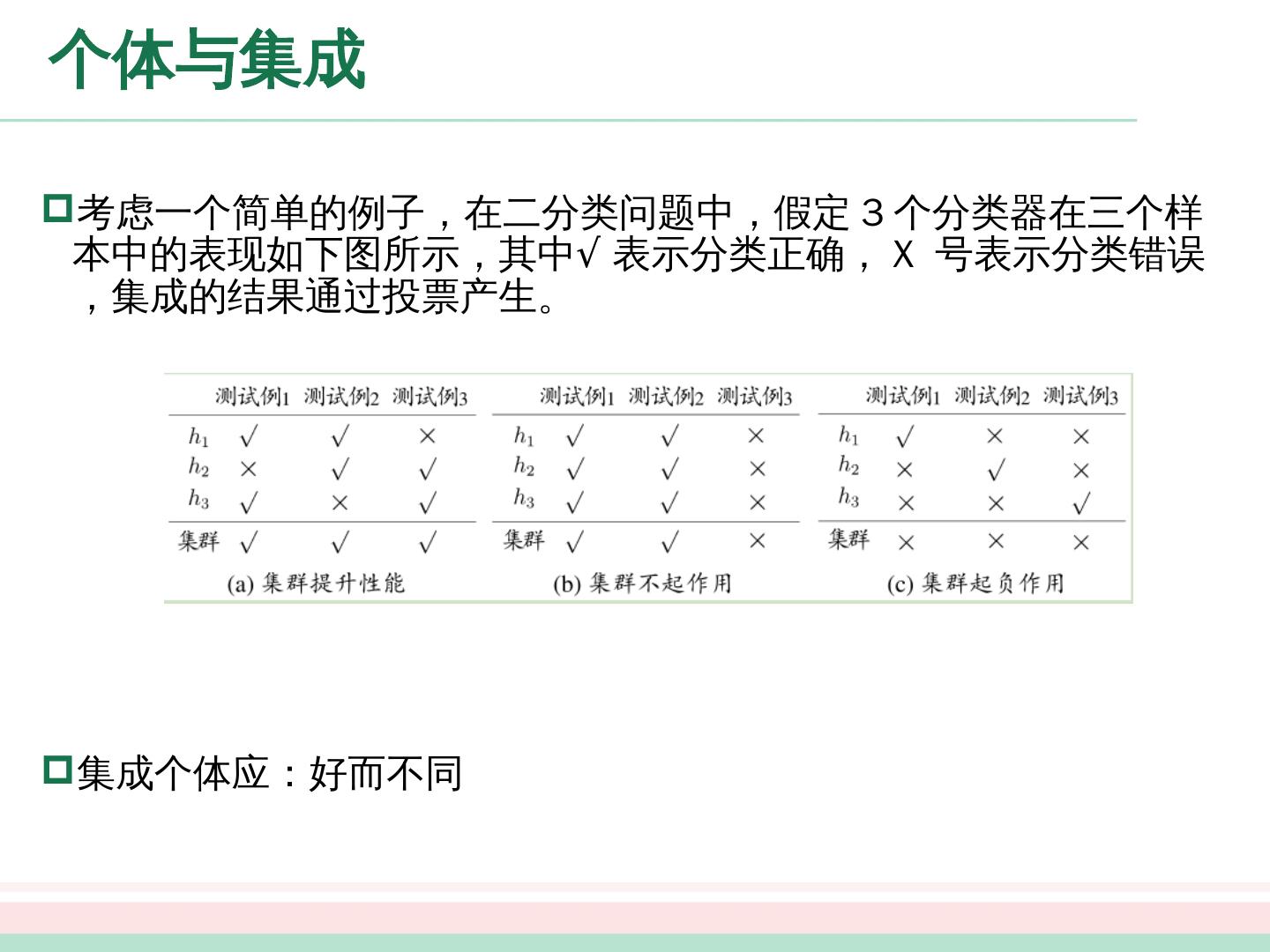
5 .个体与集成 考虑一个简单的例子，在二分类问题中，假定 3 个分类器在三个样本中的表现如下图所示，其中 √ 表示分类正确， X 号表示分类错误，集成的结果通过投票产生。 集成个体应：好而不同
6 .个体与 集成 – 简单分析 考虑二分类问题，假设基分类器的错误率为： 假设集成通过简单投票法结合 分类器，若有超过半数的基分类器正确则分类就正确
7 .个体与 集成 – 简单分析 假设基分类器的错误率相互独立，则由 Hoeffding 不等式可得集成的错误率为： 显示，在一定条件下，随着集成分类器数目的增加，集成的错误率将指数级下降，最终趋向于 0
8 .个体与集成 – 简单分析 上面的分析有一个关键假设：基学习器的误差相互独立 现实任务中，个体学习器是为解决同一个问题训练出来的，显然不可能互相独立 事实上，个体学习器的“准确性”和“多样性”本身就存在冲突 如何产生“好而不同”的个体学习器是集成学习研究的核心 集成学习大致可分为两大类
9 .个体与集成 – 简单分析 上面的分析有一个关键假设：基学习器的误差相互独立 现实任务中，个体学习器是为解决同一个问题训练出来的，显然不可能互相独立 事实上，个体学习器的“准确性”和“多样性”本身就存在冲突 如何产生“好而不同”的个体学习器是集成学习研究的核心 集成学习大致可分为两大类
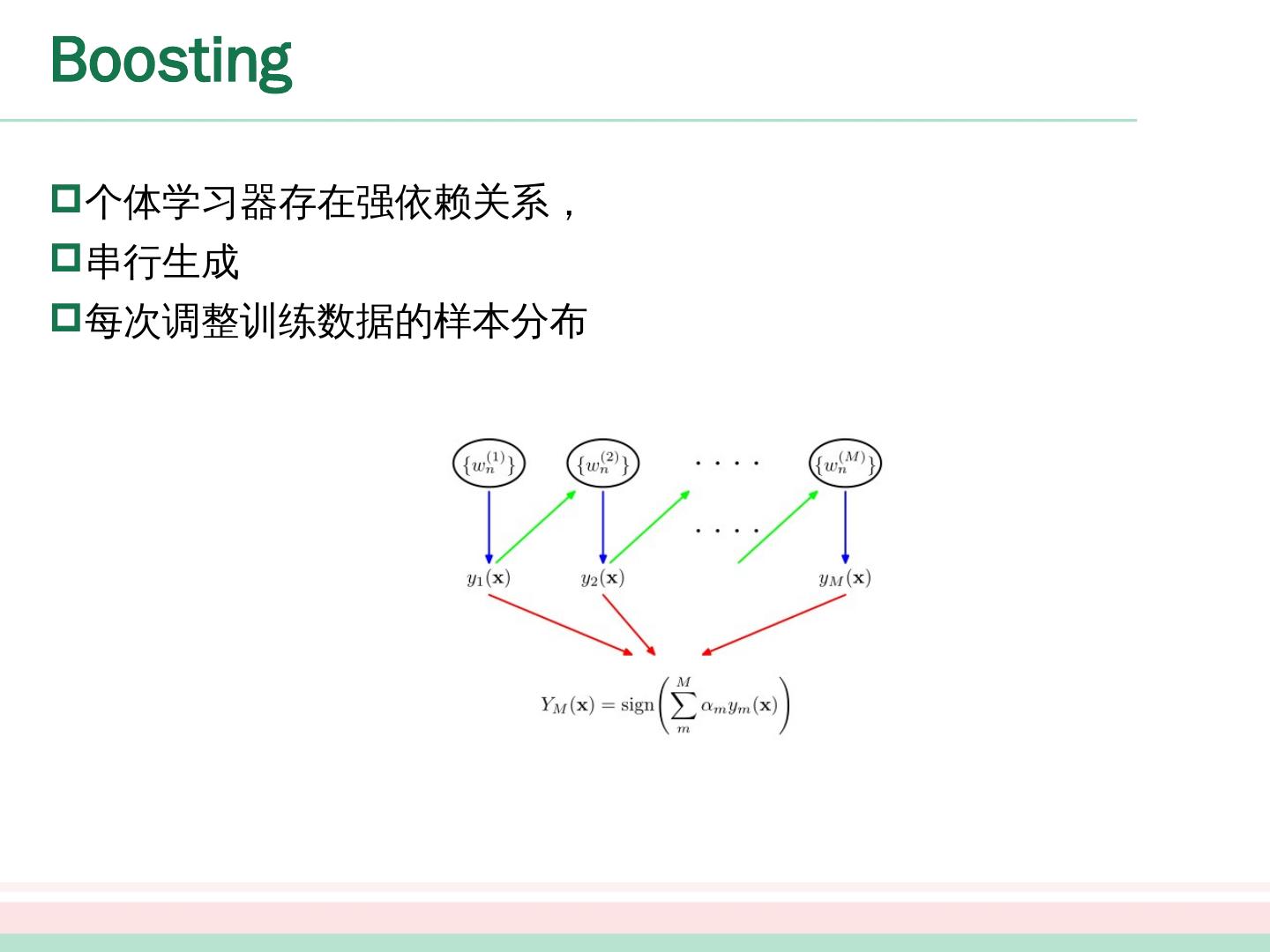
10 .Boosting 个体学习器存在强依赖 关系， 串行生成 每次调整 训练数据的 样本分布
11 .Boosting - Boosting 算法 Boosting 族算法最著名的代表是 AdaBoost
12 .Boosting – AdaBoost 算法
13 .Boosting – AdaBoost 推导 基学习器的线性组合 最小化指数损失函数
14 .Boosting – AdaBoost 推导 若 能令指数损失函数最小化，则 上式 对 的偏导值为 0 ，即 贝叶斯最优错误率，说明指数损失函数是分类任务原来 0/1 损失函数的一致的替代函数。
15 .Boosting – AdaBoost 推导 当基分类器 分布 ，该基分类器的权重 使得 最小化指数损失函数 令指数 损失函数的导数为 0 ，即
16 .Boosting – AdaBoost 推导 在获得 的样本分布进行调整，使得下一轮的基学习器 能纠正 的一些错误，理想的 能纠正全部错误 泰勒展开近似为
17 .Boosting – AdaBoost 推导 于是，理想的基学习器： 注意到 是一个常数，令 D t 表示一个分布 :
18 .Boosting – AdaBoost 推导 根据数学期望的定义，这等价于令 : 由 :
19 .Boosting – AdaBoost 推导 最终的样本分布更新 公式 则理想的基学习器
20 .Boosting – AdaBoost 注意事项 数据分布的学习 重赋权法 重采样法 重启动，避免训练过程过早停止
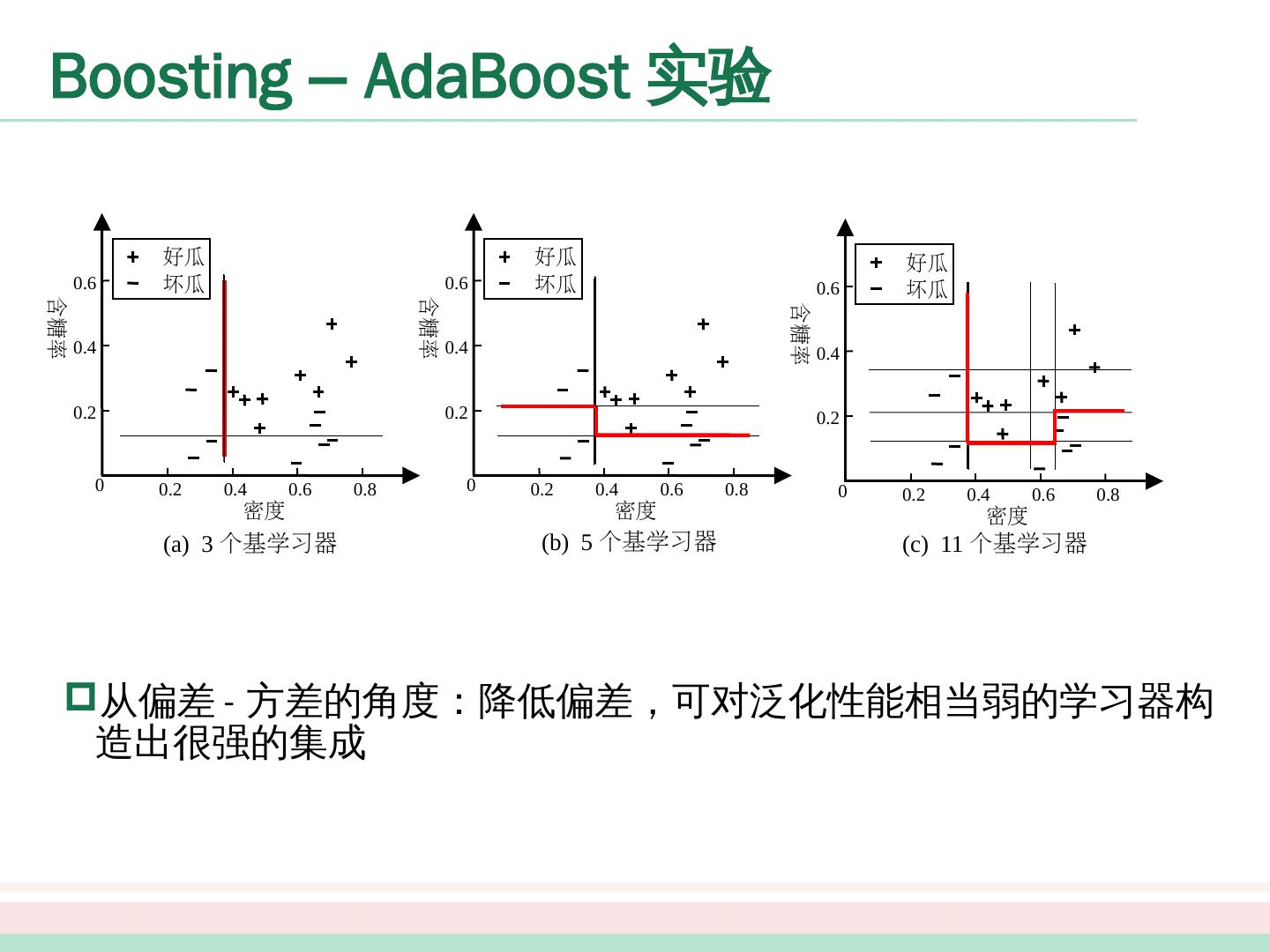
21 .0 0.2 0.4 0.6 0.8 0.2 0.4 0.6 好瓜 坏瓜 密度 含糖率 0 0.2 0.4 0.6 0.8 0.2 0.4 0.6 好瓜 坏瓜 密度 含糖率 0 0.2 0.4 0.6 0.8 0.2 0.4 0.6 好瓜 坏瓜 密度 含糖率 (a) 3 个基学习器 (b) 5 个基学习器 (c) 11 个基学习器 Boosting – AdaBoost 实验 从偏差 - 方差的角度：降低偏差，可对泛化性能相当弱的学习器构造出很强的集成
22 .0 0.2 0.4 0.6 0.8 0.2 0.4 0.6 好瓜 坏瓜 密度 含糖率 0 0.2 0.4 0.6 0.8 0.2 0.4 0.6 好瓜 坏瓜 密度 含糖率 0 0.2 0.4 0.6 0.8 0.2 0.4 0.6 好瓜 坏瓜 密度 含糖率 (a) 3 个基学习器 (b) 5 个基学习器 (c) 11 个基学习器 Boosting – AdaBoost 实验 从偏差 - 方差的角度：降低偏差，可对泛化性能相当弱的学习器构造出很强的集成
23 .Bagging 与随机森林 个体学习 器不存在 强依赖 关系 并行 化生成 自助采样法
24 .Bagging 与随机森林 - Bagging 算法
25 .Bagging 与随机 森林 - Bagging 算法特点 时间复杂度低 假定基学习器的计算复杂度为 O(m) ，采样与投票 / 平均过程的复杂度为 O(s) ，则 bagging 的复杂度大致为 T(O(m)+O(s )) 由于 O(s) 很 小且 T 是一个不大的常数 因此训练一个 bagging 集成与直接使用基学习器的复杂度同阶 可使用包外估计
26 .Bagging 与随机 森林 - 包外估计 表示对样本 包外预测，即仅考虑那些未使用样本 训练的基学习器在 预测 Bagging 泛化误差的包外估计为：
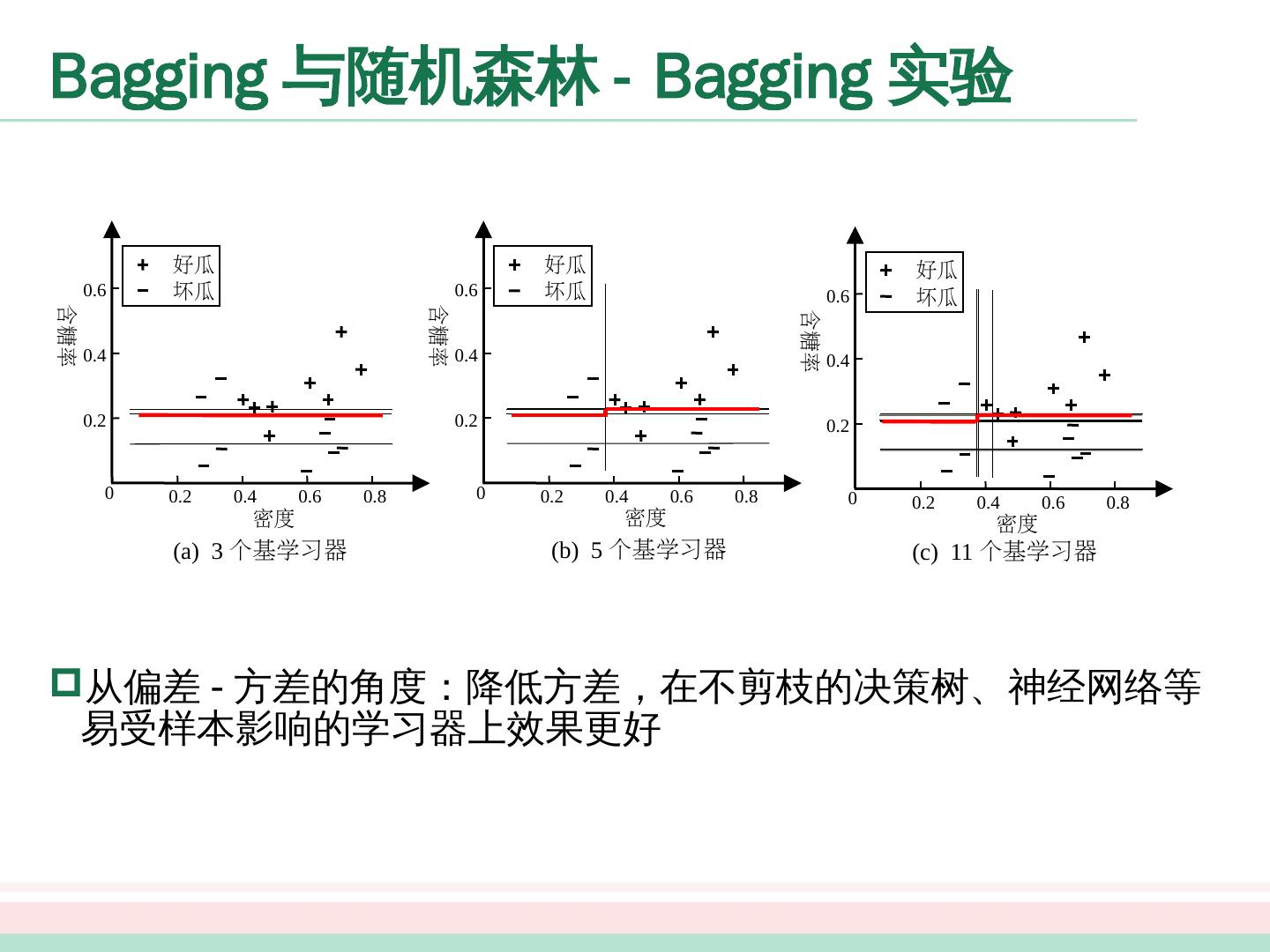
27 .0 0.2 0.4 0.6 0.8 0.2 0.4 0.6 好瓜 坏瓜 密度 含糖率 0 0.2 0.4 0.6 0.8 0.2 0.4 0.6 好瓜 坏瓜 密度 含糖率 0 0.2 0.4 0.6 0.8 0.2 0.4 0.6 好瓜 坏瓜 密度 含糖率 (a) 3 个基学习器 (b) 5 个基学习器 (c) 11 个基学习器 Bagging 与随机森林 - Bagging 实验 从偏差 - 方差的角度：降低 方差，在不剪枝的决策树、神经网络等易受样本影响的学习器上效果更好
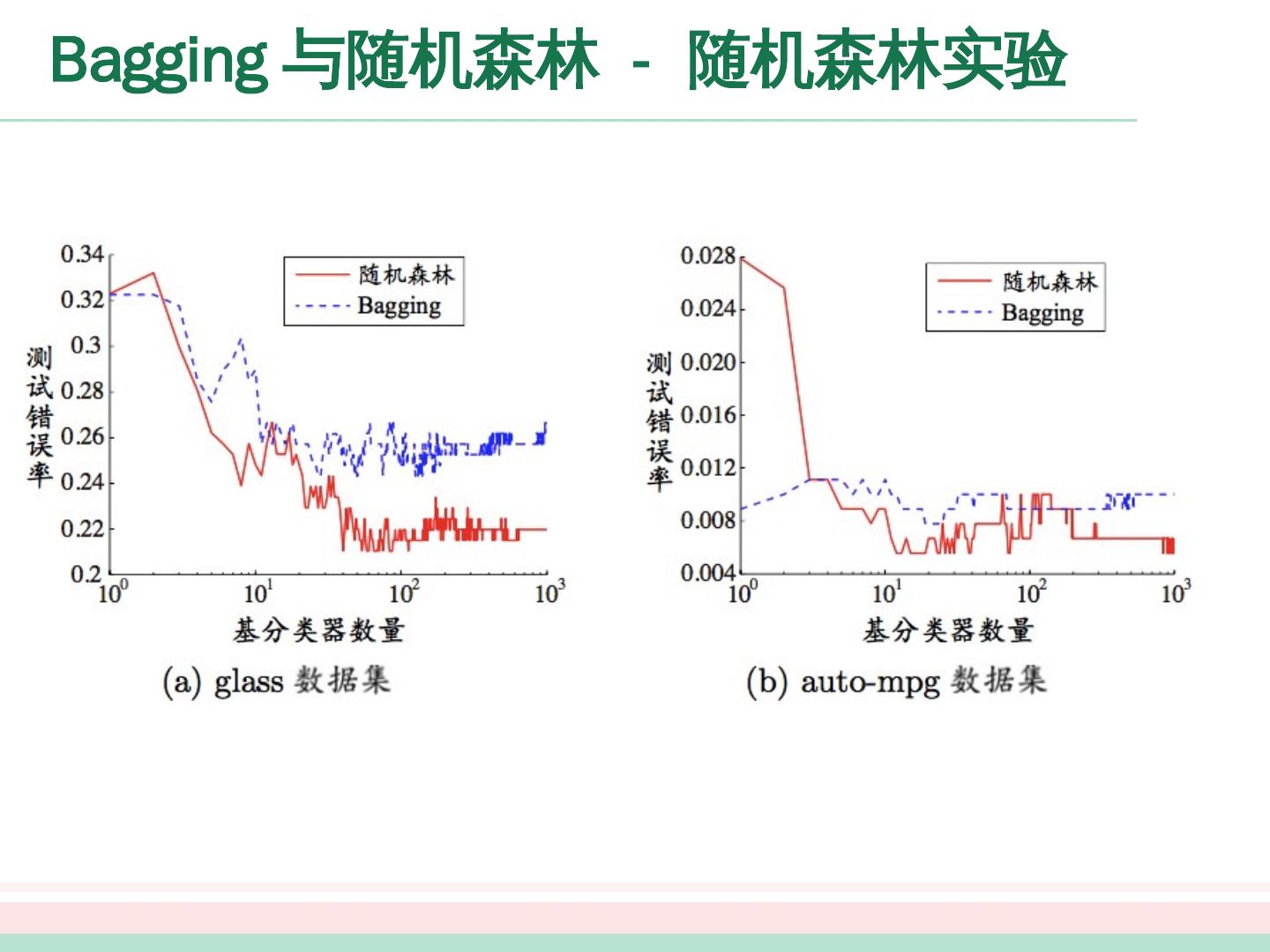
28 .Bagging 与随机森林 - 随机森林 随机森林 (Random Forest ，简称 RF) 是 bagging 的一个扩展变种 采样的随机性 属性选择的随机性
29 .Bagging 与随机 森林 - 随机森林算法 随机森林算法
热门城市
