- 快召唤伙伴们来围观吧
- 微博 QQ QQ空间 贴吧
- 文档嵌入链接
- <iframe src="https://www.slidestalk.com/u37/Federated_Machine_Learning_Intro?embed" frame border="0" width="640" height="360" scrolling="no" allowfullscreen="true">复制
- 微信扫一扫分享
联邦学习的研究与应用
联邦学习的研究与应用
• 联邦学习 Federated Machine Learning
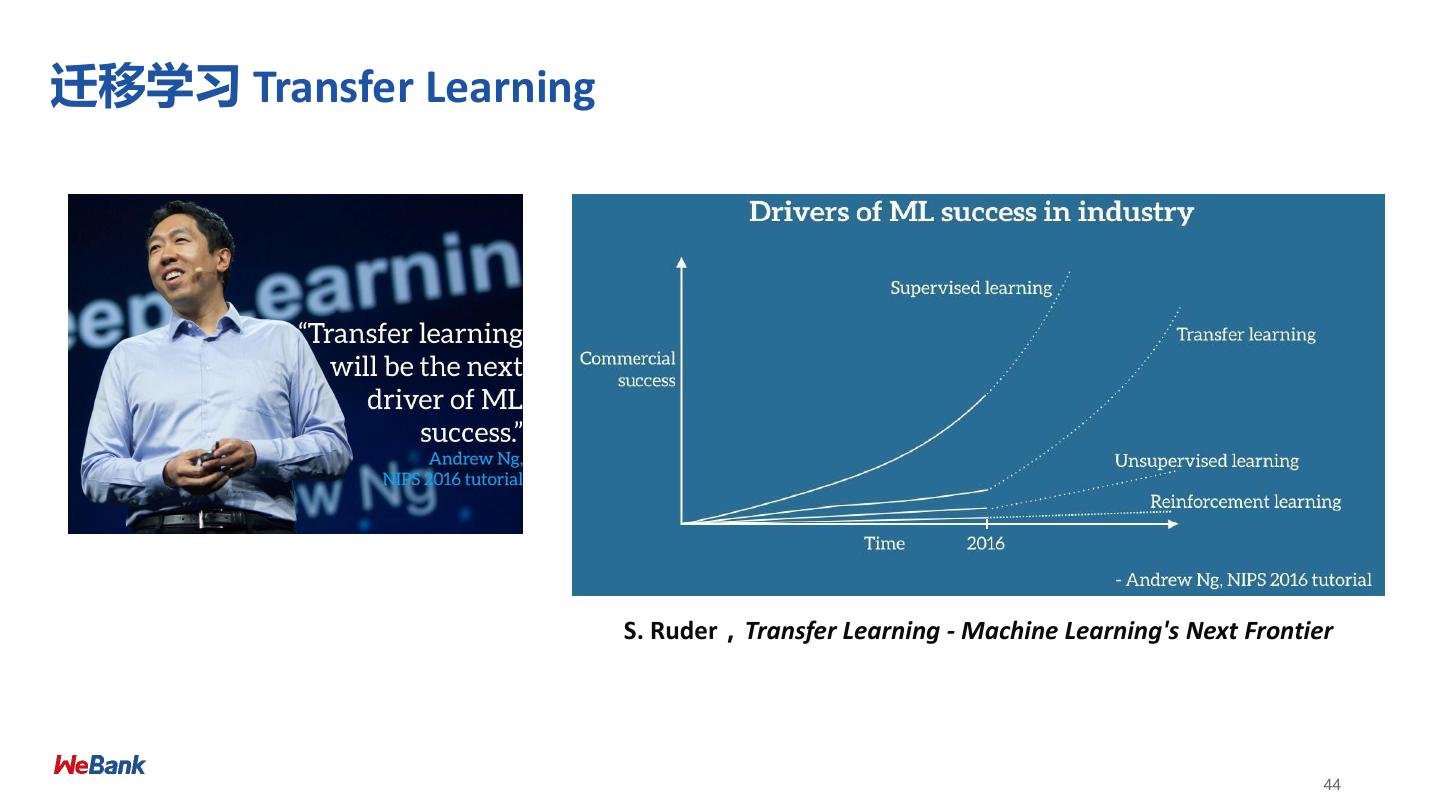
• 联邦迁移学习 Federated Transfer Learning
• 联邦学习的应用案例
• Federated AI Technology Enabler (FATE) 开源项目详解
展开查看详情
1 .CCF-TF 14 联邦学习的研究与应用 刘洋 范涛 微众银行高级研究员 yangliu@webank.com, dylanfan@webank.com https://www.fedai.org/ 2019.03
2 .提纲 • 联邦学习 Federated Machine Learning • 联邦迁移学习 Federated Transfer Learning • 联邦学习的应用案例 • Federated AI Technology Enabler (FATE) 开源项目详解 2
3 .01 Federated Learning 大规模用户在保护数据隐私下的协同学习 3
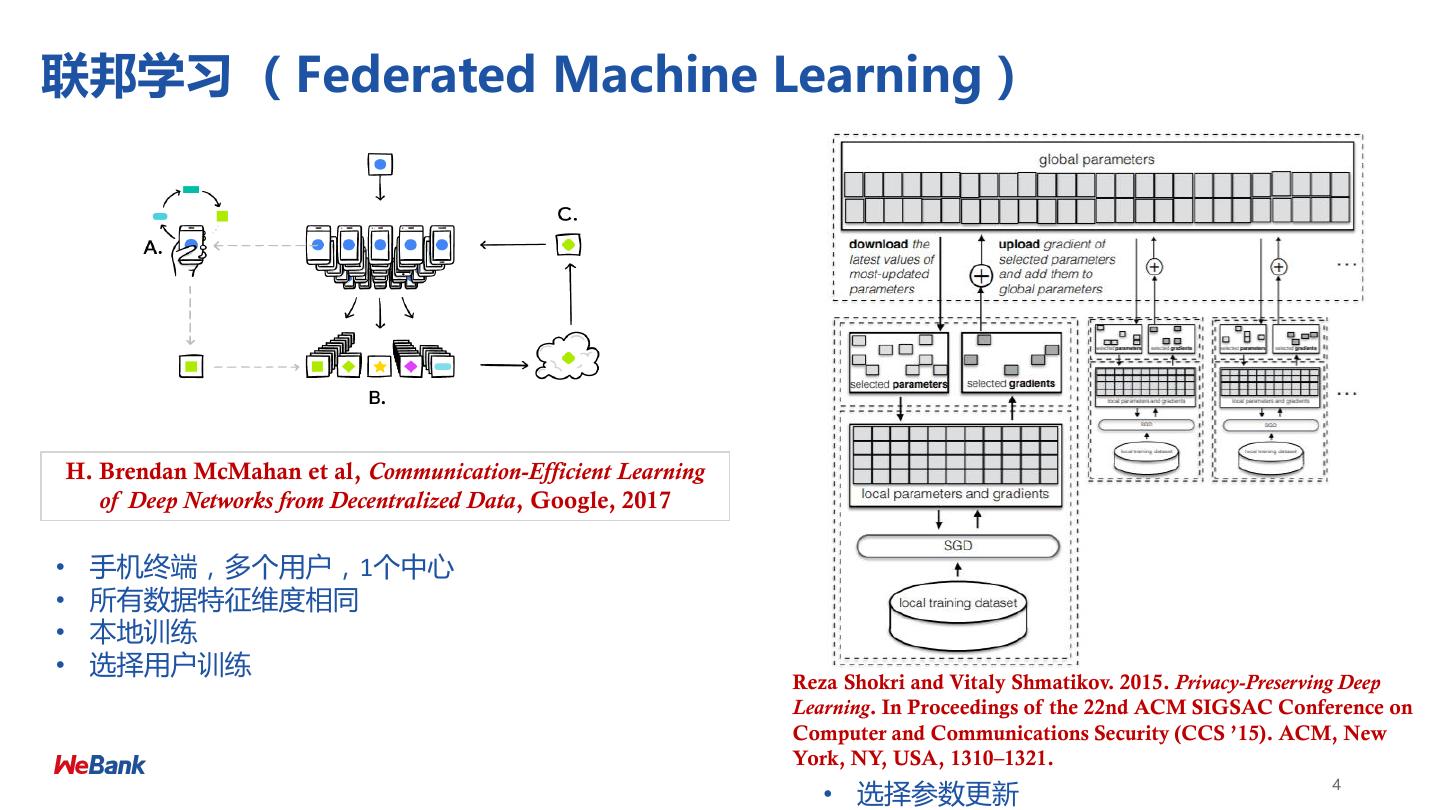
4 .联邦学习 (Federated Machine Learning) H. Brendan McMahan et al, Communication-Efficient Learning of Deep Networks from Decentralized Data, Google, 2017 • 手机终端,多个用户,1个中心 • 所有数据特征维度相同 • 本地训练 • 选择用户训练 Reza Shokri and Vitaly Shmatikov. 2015. Privacy-Preserving Deep Learning. In Proceedings of the 22nd ACM SIGSAC Conference on Computer and Communications Security (CCS ’15). ACM, New York, NY, USA, 1310–1321. 4 • 选择参数更新
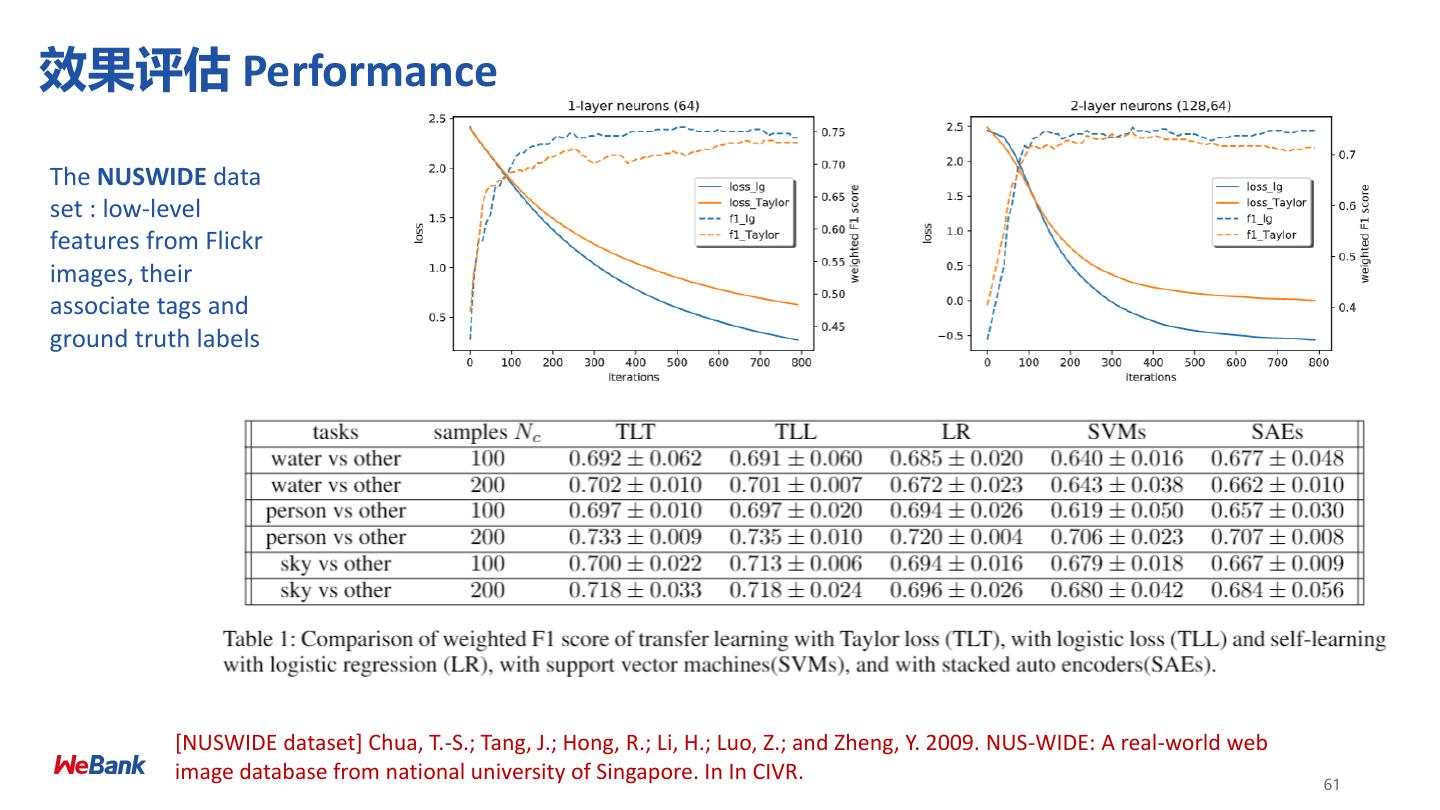
5 .联邦学习 (Federated Machine Learning)的研究进展 • 系统效率 • 模型压缩 Compression [KMY16] • 算法优化 Optimization algorithms [KMR16] • 参与方选取 Client selection [NY18] • 边缘计算 Resource constraint, IoT, Edge computing [WTS18] • 模型效果 • 数据分布不均匀 Data distribution and selection [ZLL18] • 个性化 Personalization [SCS18] • 数据安全 5
6 . 梯度是否泄露信息? 同态加密保护梯度更新 Le Trieu Phong, Yoshinori Aono, Takuya Hayashi, Lihua Wang, and Shiho Moriai. 2018. Privacy-Preserving Deep Learning via Additively Homomorphic Encryption. IEEE Trans. Information Forensics and Security,13, 5 * Q. Yang, Y. Liu, T. Chen & Y. Tong, Federated machine learning: (2018),1333–1345 Concepts and applications, ACM Transactions on Intelligent Systems and Technology (TIST) 10(2), 12:1-12:19, 2019 6
7 .Secure Aggregation [BIK+17] • 本地训练 Local training • 秘密共享 Secret share aggregated update • 稳定性 Robust to vanishing clients • 无个人梯度信息泄露 Individual gradient not disclosed • 半诚实假设 honest-but-curious setting, server does not collude with users [BIK+17] Bonawitz, K., Ivanov, V., Kreuter, B., Marcedone, A., McMahan, H. B., Patel, S., ... & Seth, K. (2017, October). Practical secure aggregation for privacy-preserving machine learning. In Proceedings of the 2017 ACM SIGSAC Conference on Computer and Communications Security (pp. 1175-1191). ACM. 7
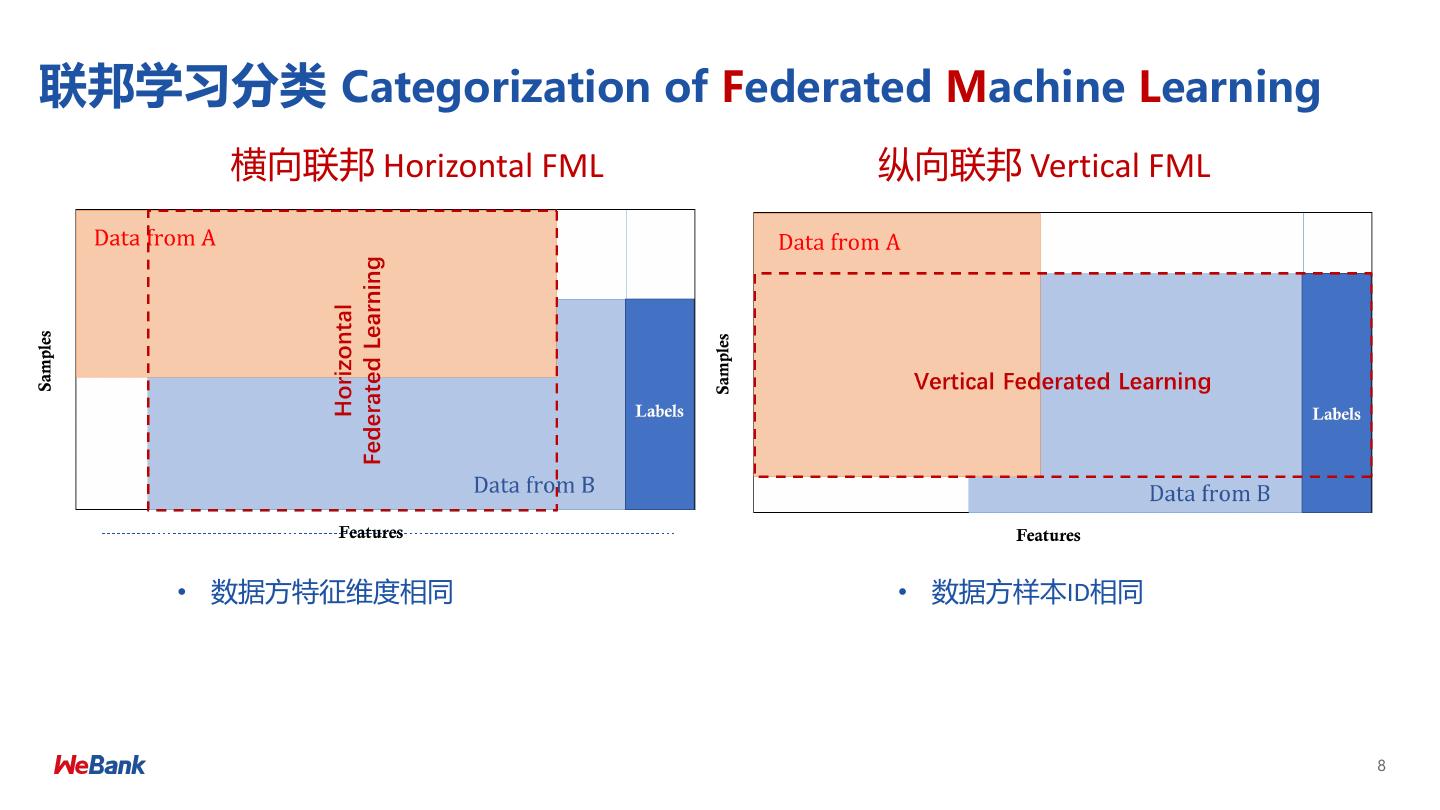
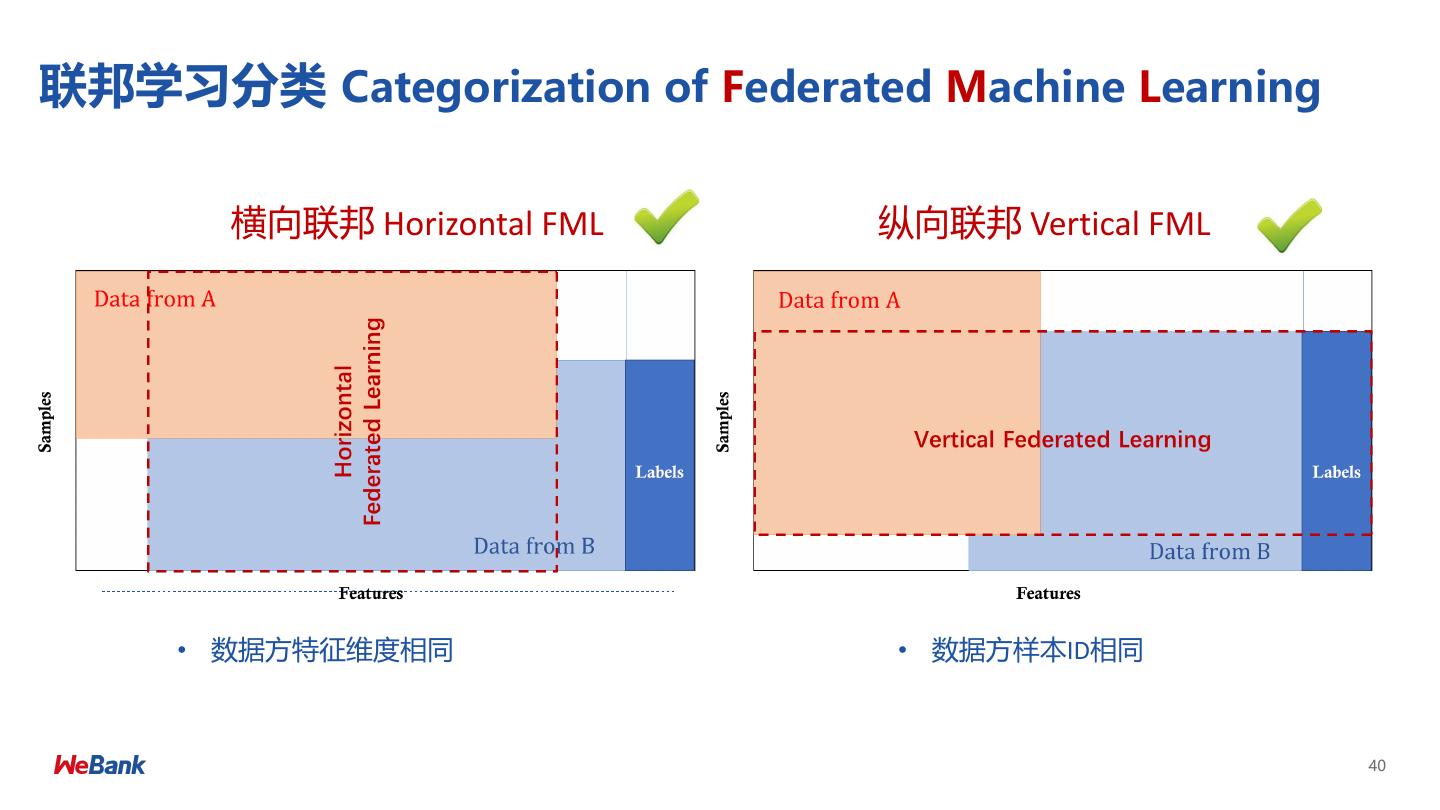
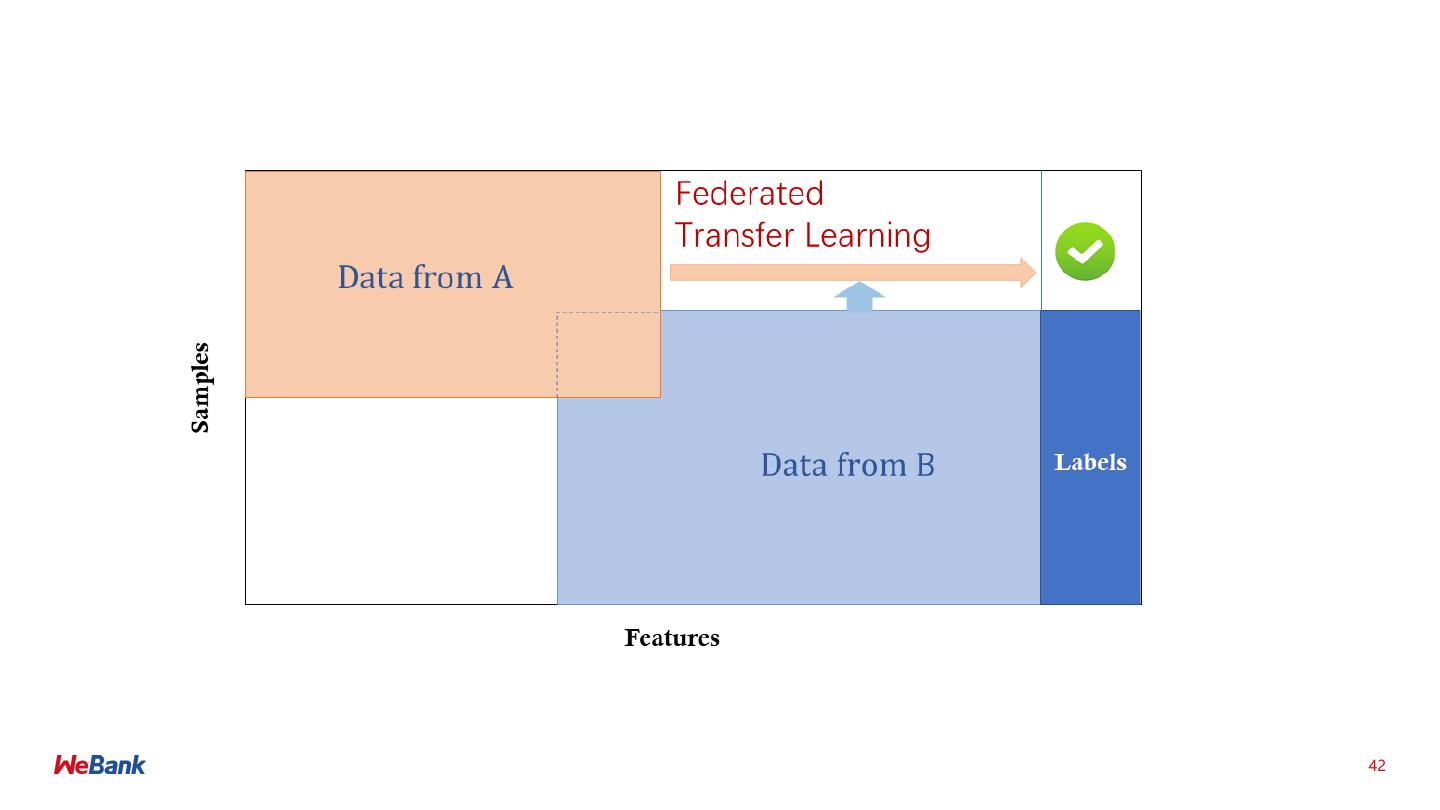
8 .联邦学习分类 Categorization of Federated Machine Learning 横向联邦 Horizontal FML 纵向联邦 Vertical FML • 数据方特征维度相同 • 数据方样本ID相同 8
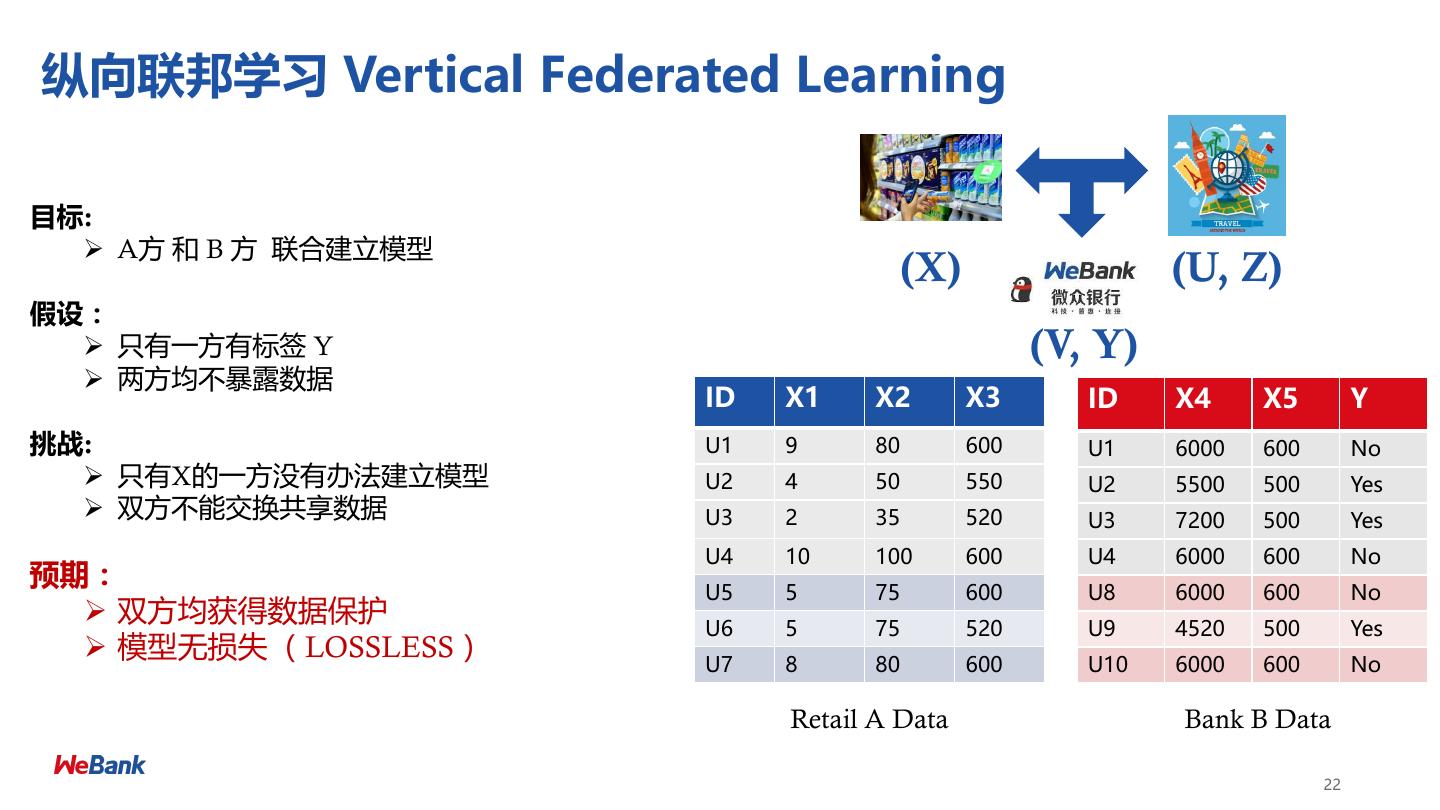
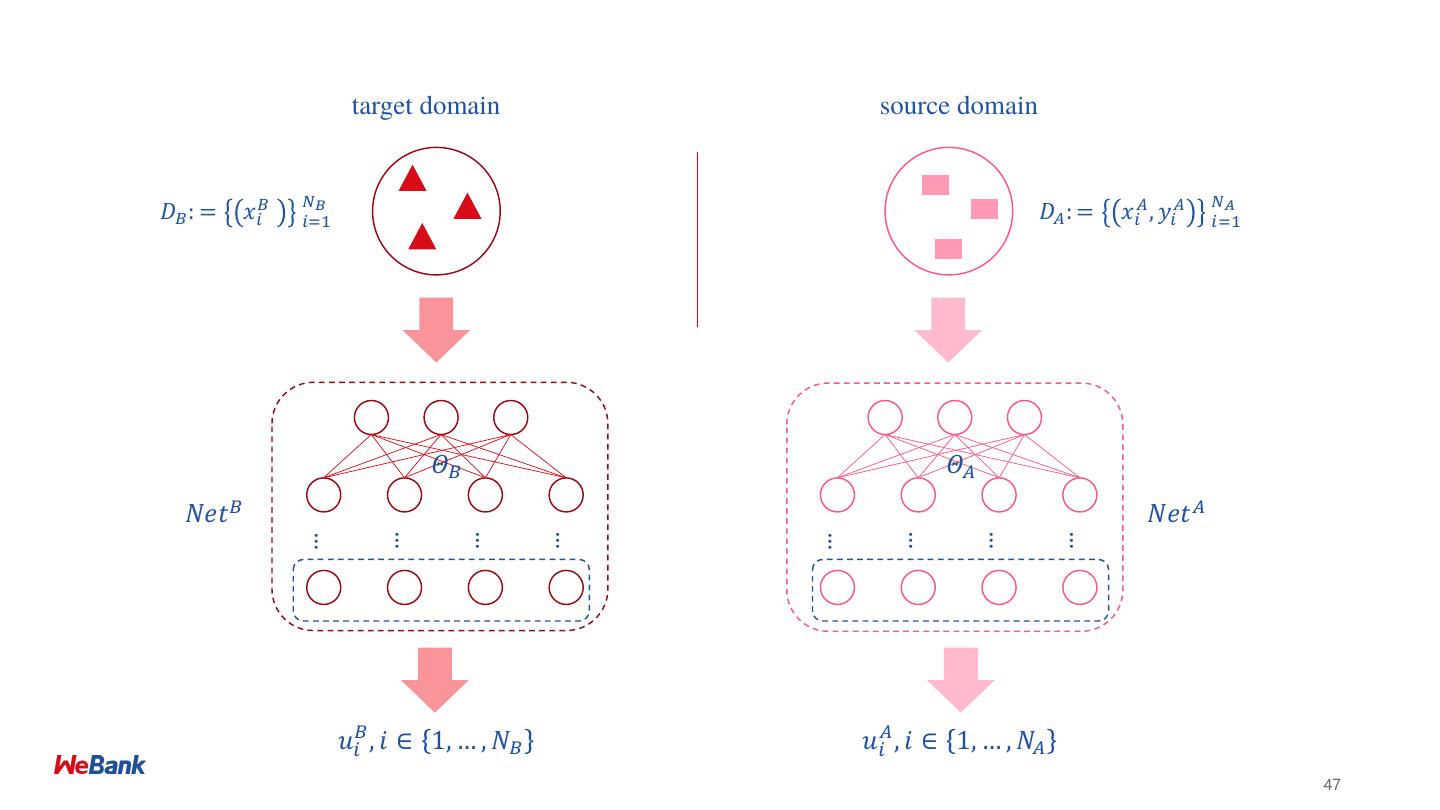
9 .纵向联邦学习 Vertical Federated Learning 目标: ➢ A方 和 B 方 联合建立模型 (X) (U, Z) 假设: ➢ 只有一方有标签 Y (V, Y) ➢ 两方均不暴露数据 ID X1 X2 X3 ID X4 X5 Y 挑战: U1 9 80 600 U1 6000 600 No ➢ 只有X的一方没有办法建立模型 U2 4 50 550 U2 5500 500 Yes ➢ 双方不能交换共享数据 U3 2 35 520 U3 7200 500 Yes U4 10 100 600 U4 6000 600 No 预期: U5 5 75 600 U8 6000 600 No ➢ 双方均获得数据保护 U6 5 75 520 U9 4520 500 Yes ➢ 模型无损失 (LOSSLESS) U7 8 80 600 U10 6000 600 No Retail A Data Bank B Data 9
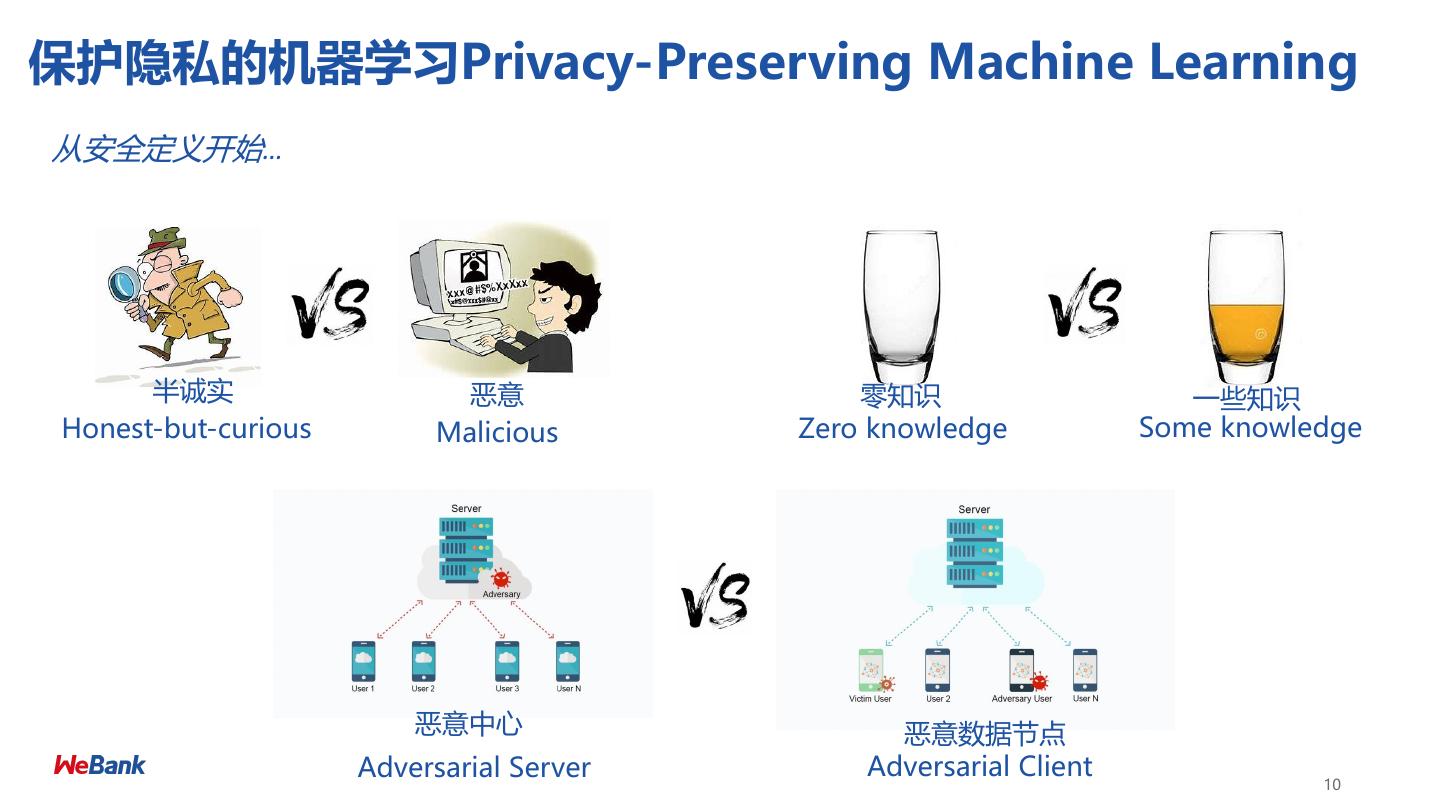
10 .保护隐私的机器学习Privacy-Preserving Machine Learning 从安全定义开始… 半诚实 恶意 零知识 一些知识 Honest-but-curious Malicious Zero knowledge Some knowledge 恶意中心 恶意数据节点 Adversarial Server Adversarial Client 10
11 .隐私保护下的技术工具 • 多方安全计算 Secure Multi-party Computation (MPC) • 同态加密 Homomorphic Encryption (HE) • 姚式混淆电路 Yao’s Garbled Circuit • 秘密共享 Secret Sharing • 差分隐私 Differential Privacy (DP) …… 11
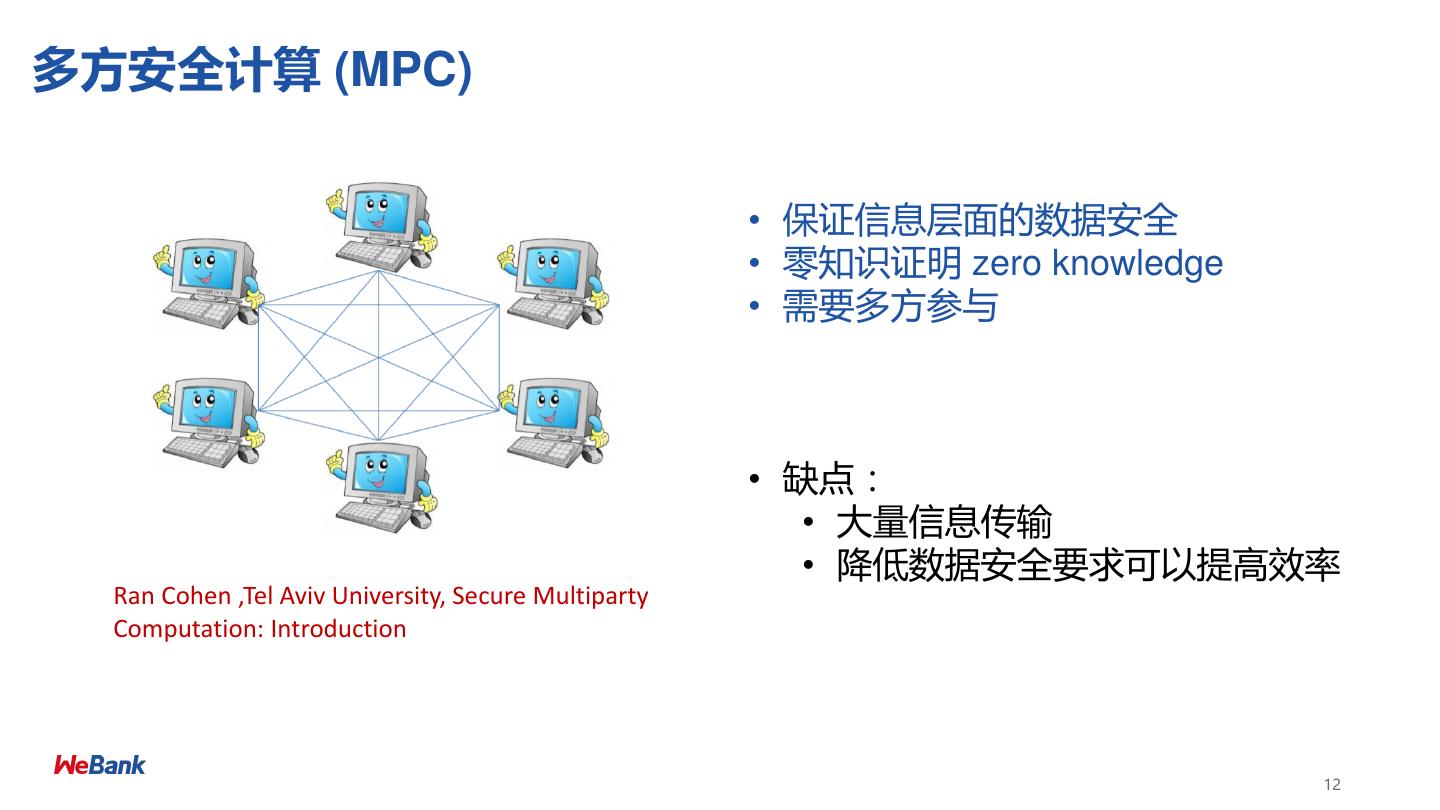
12 .多方安全计算 (MPC) • 保证信息层面的数据安全 • 零知识证明 zero knowledge • 需要多方参与 • 缺点: • 大量信息传输 • 降低数据安全要求可以提高效率 Ran Cohen ,Tel Aviv University, Secure Multiparty Computation: Introduction 12
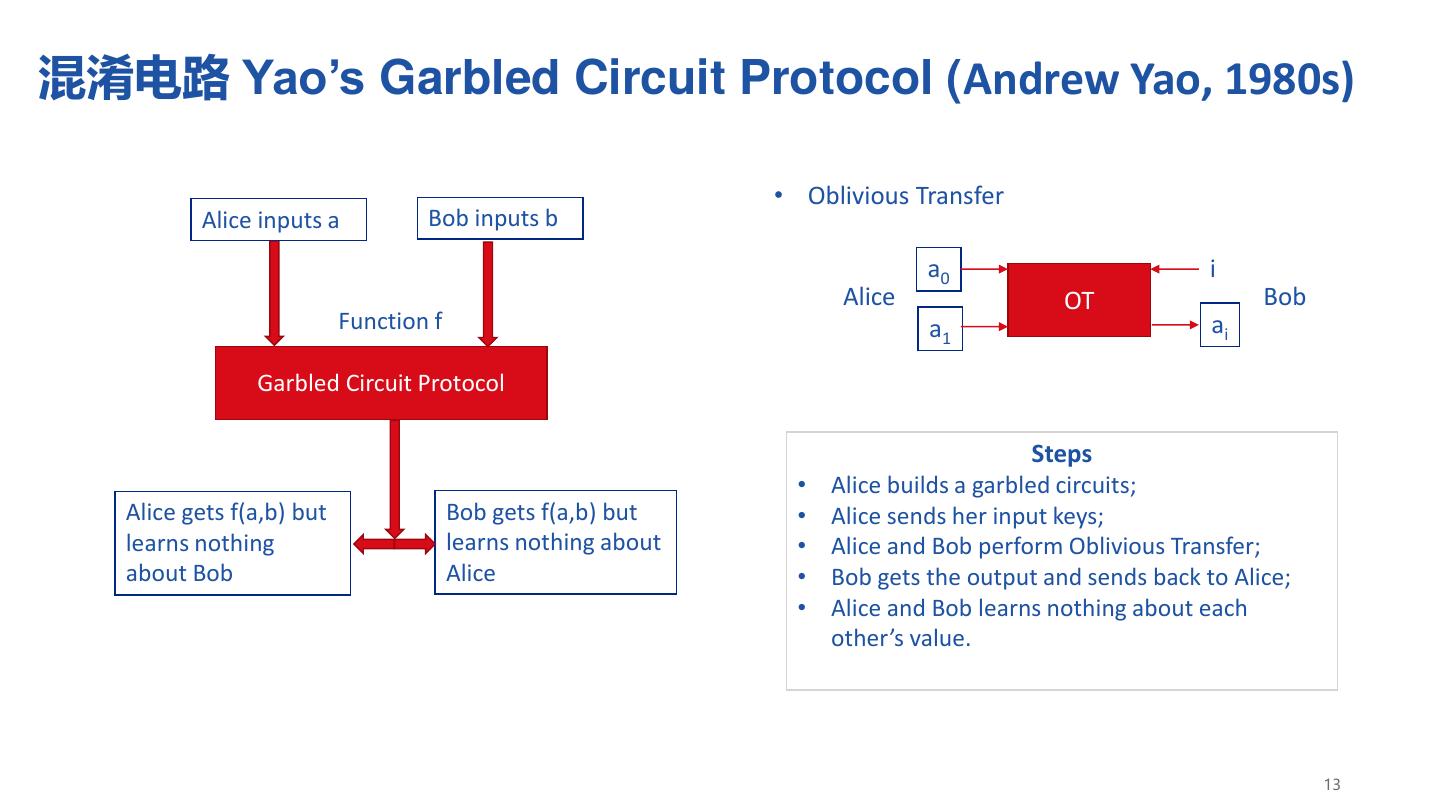
13 .混淆电路 Yao’s Garbled Circuit Protocol (Andrew Yao, 1980s) • Oblivious Transfer Alice inputs a Bob inputs b a0 i Alice OT Bob Function f a1 ai Garbled Circuit Protocol Steps • Alice builds a garbled circuits; Alice gets f(a,b) but Bob gets f(a,b) but • Alice sends her input keys; learns nothing learns nothing about • Alice and Bob perform Oblivious Transfer; about Bob Alice • Bob gets the output and sends back to Alice; • Alice and Bob learns nothing about each other’s value. 13
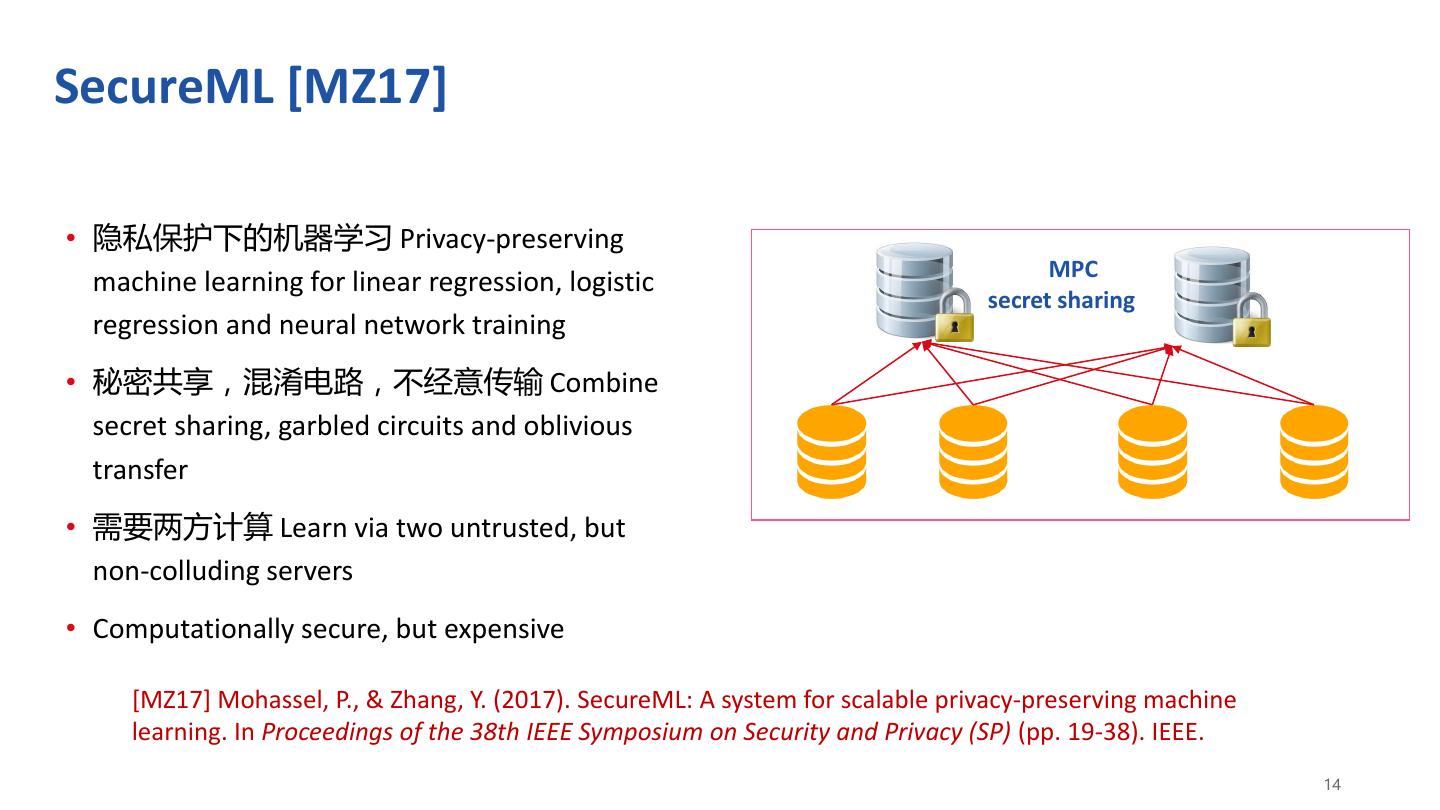
14 .SecureML [MZ17] • 隐私保护下的机器学习 Privacy-preserving MPC machine learning for linear regression, logistic secret sharing regression and neural network training • 秘密共享,混淆电路,不经意传输 Combine secret sharing, garbled circuits and oblivious transfer • 需要两方计算 Learn via two untrusted, but non-colluding servers • Computationally secure, but expensive [MZ17] Mohassel, P., & Zhang, Y. (2017). SecureML: A system for scalable privacy-preserving machine learning. In Proceedings of the 38th IEEE Symposium on Security and Privacy (SP) (pp. 19-38). IEEE. 14
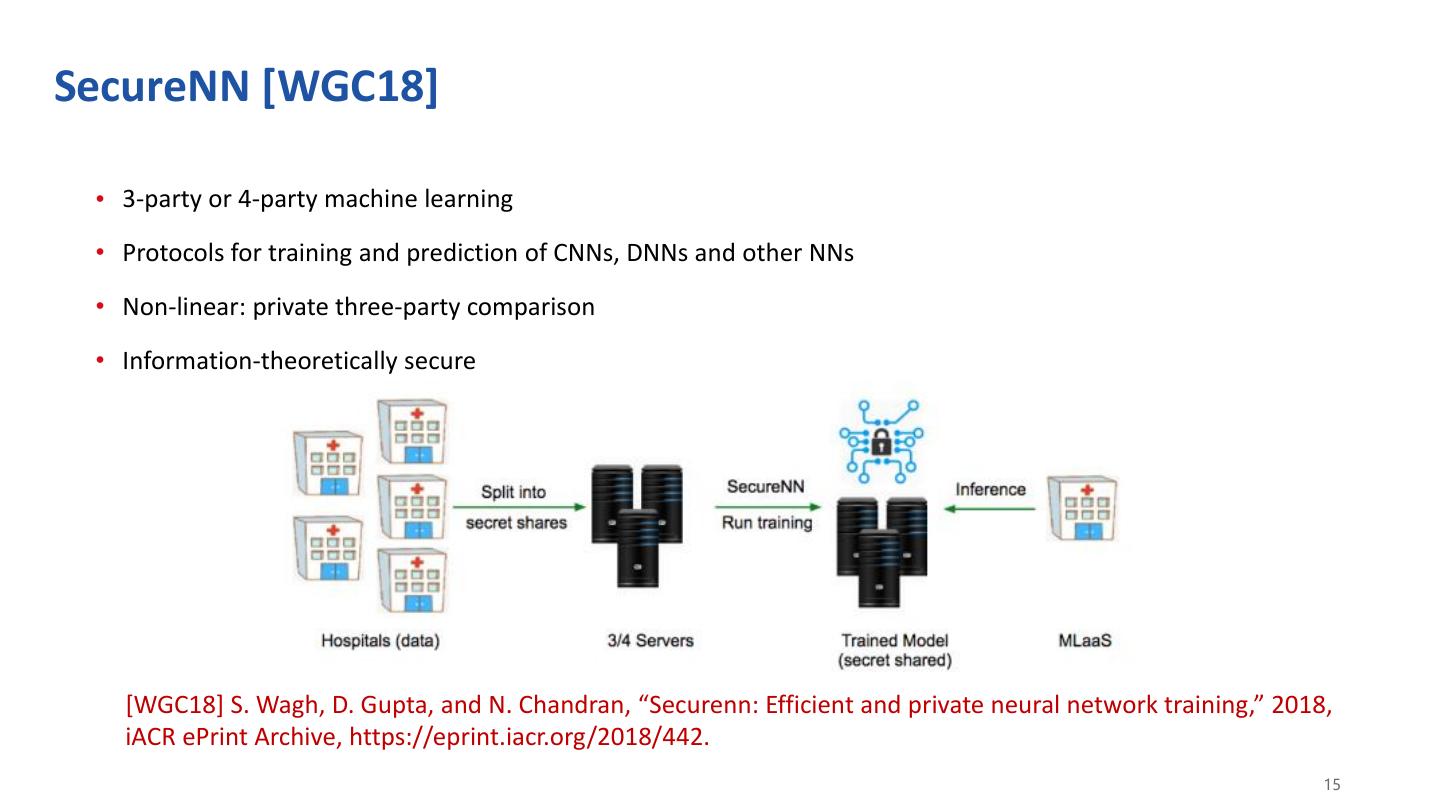
15 .SecureNN [WGC18] • 3-party or 4-party machine learning • Protocols for training and prediction of CNNs, DNNs and other NNs • Non-linear: private three-party comparison • Information-theoretically secure [WGC18] S. Wagh, D. Gupta, and N. Chandran, “Securenn: Efficient and private neural network training,” 2018, iACR ePrint Archive, https://eprint.iacr.org/2018/442. 15
16 .同态加密 Homomorphic Encryption • 全同态或者半同态 Full Homomorphic Encryption and Partial Homomorphic Encryption • 数据层面的信息保护 Data-level information protection Paillier 半同态加密 Partially homomorphic encryption Addition : [[u]] + [[v]] = [[u+v]] Scalar multiplication: n[[u]] = [[nu]] • For public key pk = n, the encoded form of m ∈ {0, . . . , n − 1} is Encode(m) = rn (1 + n) m mod n2 r is random selected from {0, . . . , n − 1}. • For float q = (s, e) , encrypt [[q]] = ([[s]], e) , here q = sβe,is base-β exponential representation. Rivest, R. L.; Adleman, L.; and Dertouzos, M. L. 1978. On data banks and privacy homomorphisms. Foundations of Secure Computation, Academia Press, 169–179. 16
17 .同态加密在机器学习上应用 Apply HE to Machine Learning ① 多项式近似 Polynomial approximation for logarithm function ② 加密计算 Encrypted computation for each term in the polynomial function 1 1 loss = log 2 − ywT x + ( wT x) 2 2 8 1 1 [[loss ]] = [[log 2]] + (− ) *[[ ywT x]] + [[(wT x) 2 ]] 2 8 • Kim, M.; Song, Y.; Wang, S.; Xia, Y.; and Jiang, X. 2018. Secure logistic regression based on homomorphic encryption: Design and evaluation. JMIR Med Inform 6(2) • Y. Aono, T. Hayashi, T. P. Le, L. Wang, Scalable and secure logistic regression via homomorphic encryption, CODASPY16 17
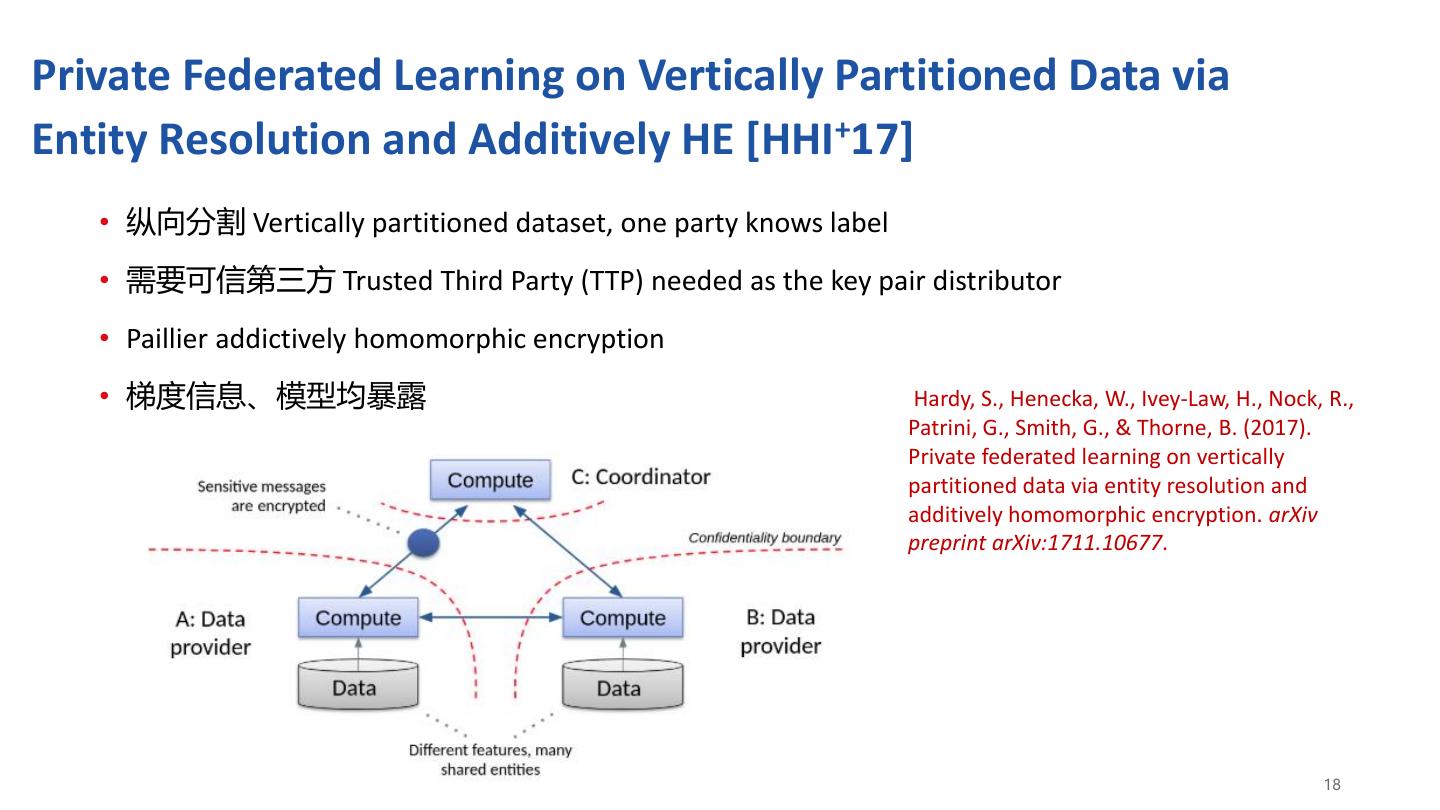
18 .Private Federated Learning on Vertically Partitioned Data via Entity Resolution and Additively HE [HHI+17] • 纵向分割 Vertically partitioned dataset, one party knows label • 需要可信第三方 Trusted Third Party (TTP) needed as the key pair distributor • Paillier addictively homomorphic encryption • 梯度信息、模型均暴露 Hardy, S., Henecka, W., Ivey-Law, H., Nock, R., Patrini, G., Smith, G., & Thorne, B. (2017). Private federated learning on vertically partitioned data via entity resolution and additively homomorphic encryption. arXiv preprint arXiv:1711.10677. 18
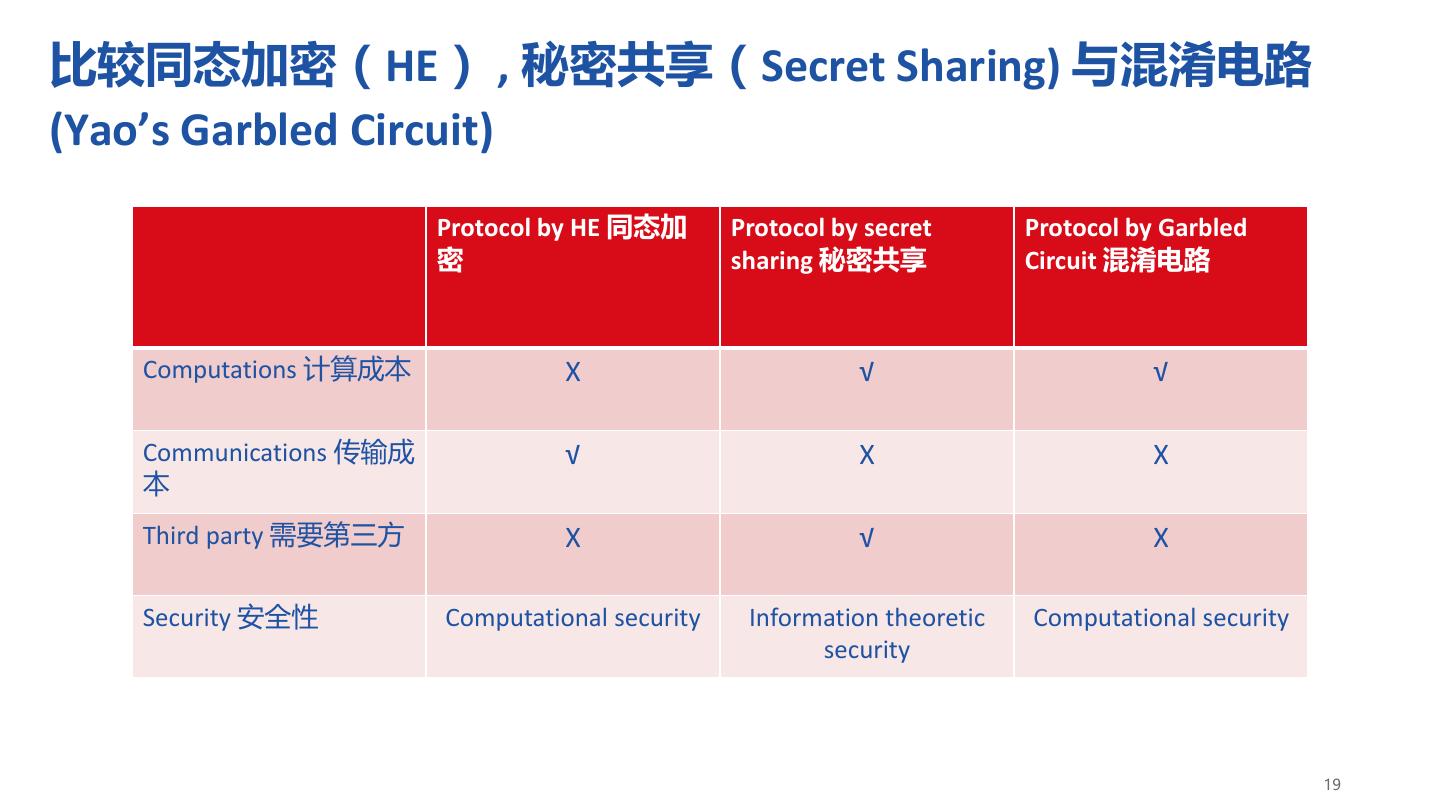
19 .比较同态加密(HE) , 秘密共享(Secret Sharing) 与混淆电路 (Yao’s Garbled Circuit) Protocol by HE 同态加 Protocol by secret Protocol by Garbled 密 sharing 秘密共享 Circuit 混淆电路 Computations 计算成本 X √ √ Communications 传输成 √ X X 本 Third party 需要第三方 X √ X Security 安全性 Computational security Information theoretic Computational security security 19
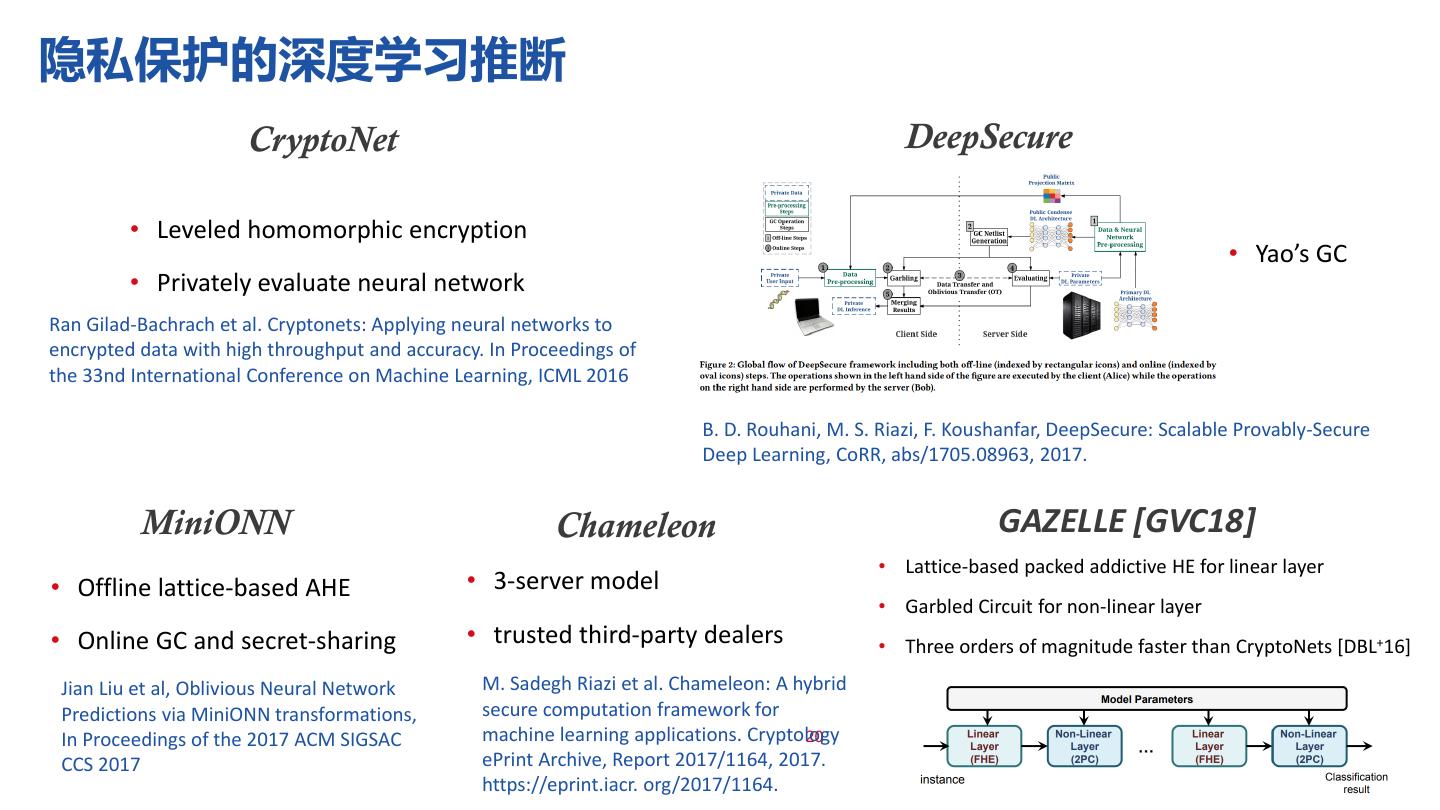
20 .隐私保护的深度学习推断 CryptoNet DeepSecure • Leveled homomorphic encryption • Yao’s GC • Privately evaluate neural network Ran Gilad-Bachrach et al. Cryptonets: Applying neural networks to encrypted data with high throughput and accuracy. In Proceedings of the 33nd International Conference on Machine Learning, ICML 2016 B. D. Rouhani, M. S. Riazi, F. Koushanfar, DeepSecure: Scalable Provably-Secure Deep Learning, CoRR, abs/1705.08963, 2017. MiniONN Chameleon GAZELLE [GVC18] • Lattice-based packed addictive HE for linear layer • Offline lattice-based AHE • 3-server model • Garbled Circuit for non-linear layer • Online GC and secret-sharing • trusted third-party dealers • Three orders of magnitude faster than CryptoNets [DBL+16] Jian Liu et al, Oblivious Neural Network M. Sadegh Riazi et al. Chameleon: A hybrid Predictions via MiniONN transformations, secure computation framework for In Proceedings of the 2017 ACM SIGSAC machine learning applications. Cryptology 20 CCS 2017 ePrint Archive, Report 2017/1164, 2017. https://eprint.iacr. org/2017/1164.
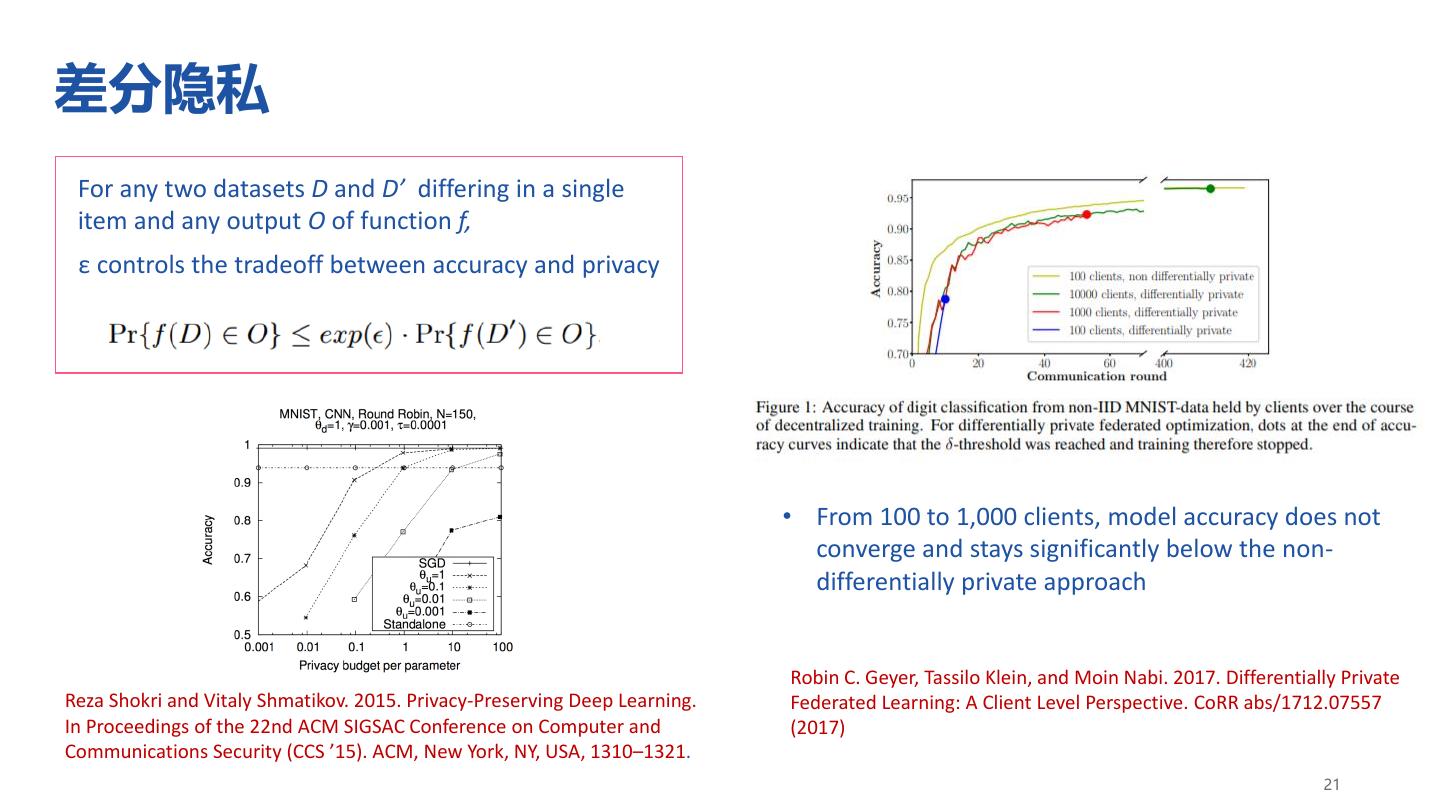
21 .差分隐私 For any two datasets D and D’ differing in a single item and any output O of function f, ε controls the tradeoff between accuracy and privacy • From 100 to 1,000 clients, model accuracy does not converge and stays significantly below the non- differentially private approach Robin C. Geyer, Tassilo Klein, and Moin Nabi. 2017. Differentially Private Reza Shokri and Vitaly Shmatikov. 2015. Privacy-Preserving Deep Learning. Federated Learning: A Client Level Perspective. CoRR abs/1712.07557 In Proceedings of the 22nd ACM SIGSAC Conference on Computer and (2017) Communications Security (CCS ’15). ACM, New York, NY, USA, 1310–1321. 21
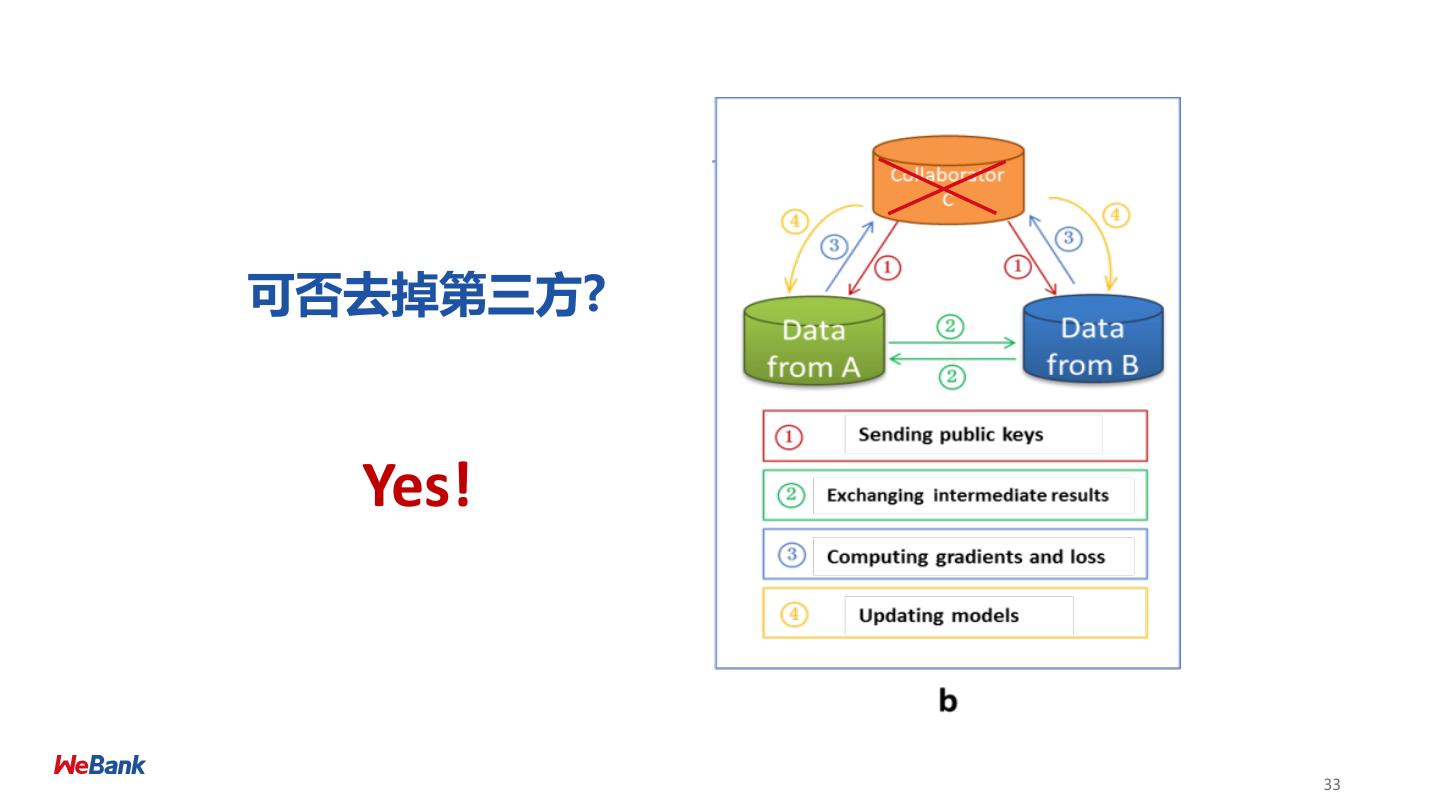
22 .纵向联邦学习 Vertical Federated Learning 目标: ➢ A方 和 B 方 联合建立模型 (X) (U, Z) 假设: ➢ 只有一方有标签 Y (V, Y) ➢ 两方均不暴露数据 ID X1 X2 X3 ID X4 X5 Y 挑战: U1 9 80 600 U1 6000 600 No ➢ 只有X的一方没有办法建立模型 U2 4 50 550 U2 5500 500 Yes ➢ 双方不能交换共享数据 U3 2 35 520 U3 7200 500 Yes U4 10 100 600 U4 6000 600 No 预期: U5 5 75 600 U8 6000 600 No ➢ 双方均获得数据保护 U6 5 75 520 U9 4520 500 Yes ➢ 模型无损失 (LOSSLESS) U7 8 80 600 U10 6000 600 No Retail A Data Bank B Data 22
23 .安全定义 Security Definition • All parties are honest-but-curious. • We assume a threat model with a semi-honest adversary who can corrupt at most one of the two data clients. • For a protocol P performing (OA,OB)=P(IA,IB), where OA and OB are party A and B's output and IA and IB are their inputs, P is secure against A if there exists an infinite number of (I'B,O'B) pairs such that (OA,O'B)=P(IA,I'B). • A practical solution to control information disclosure. 23
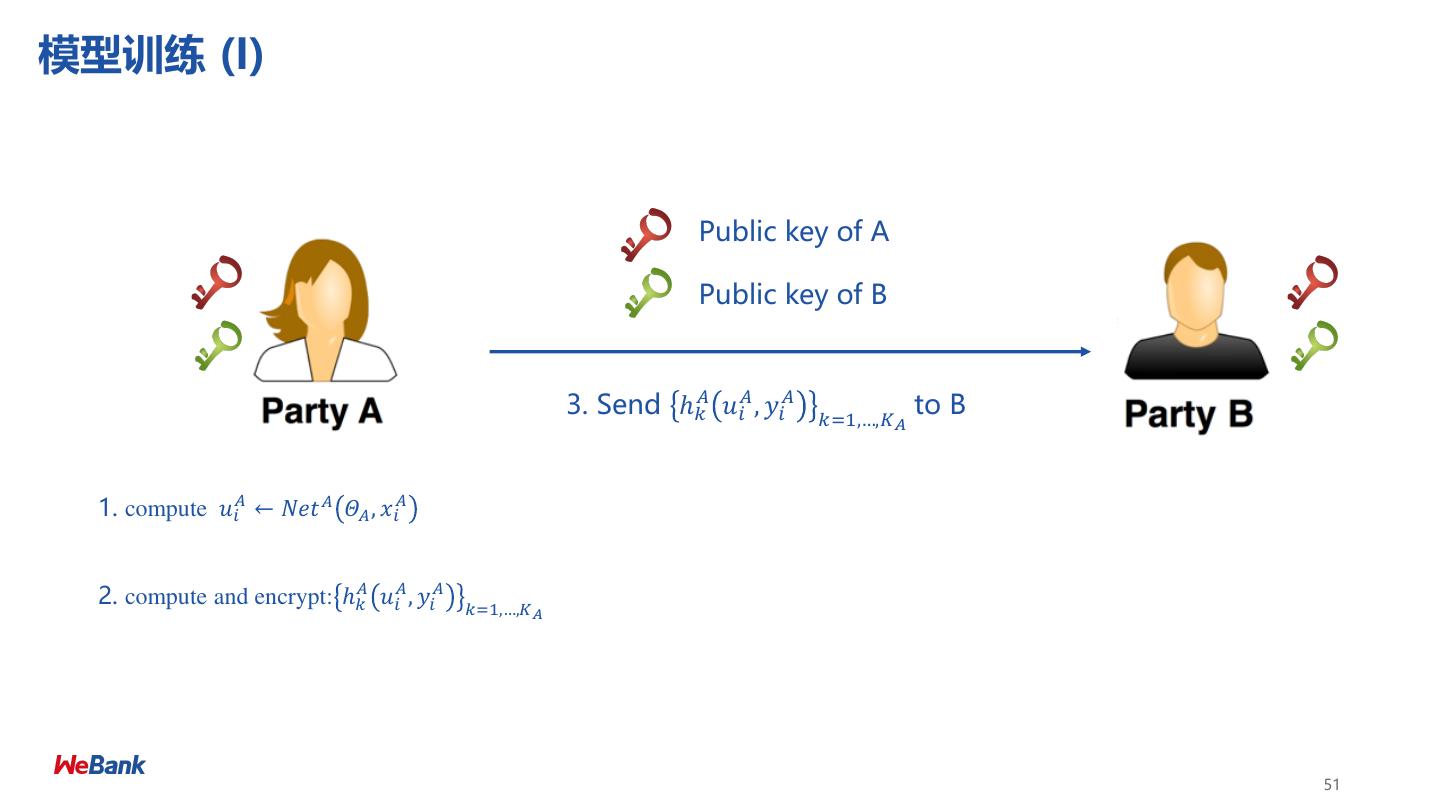
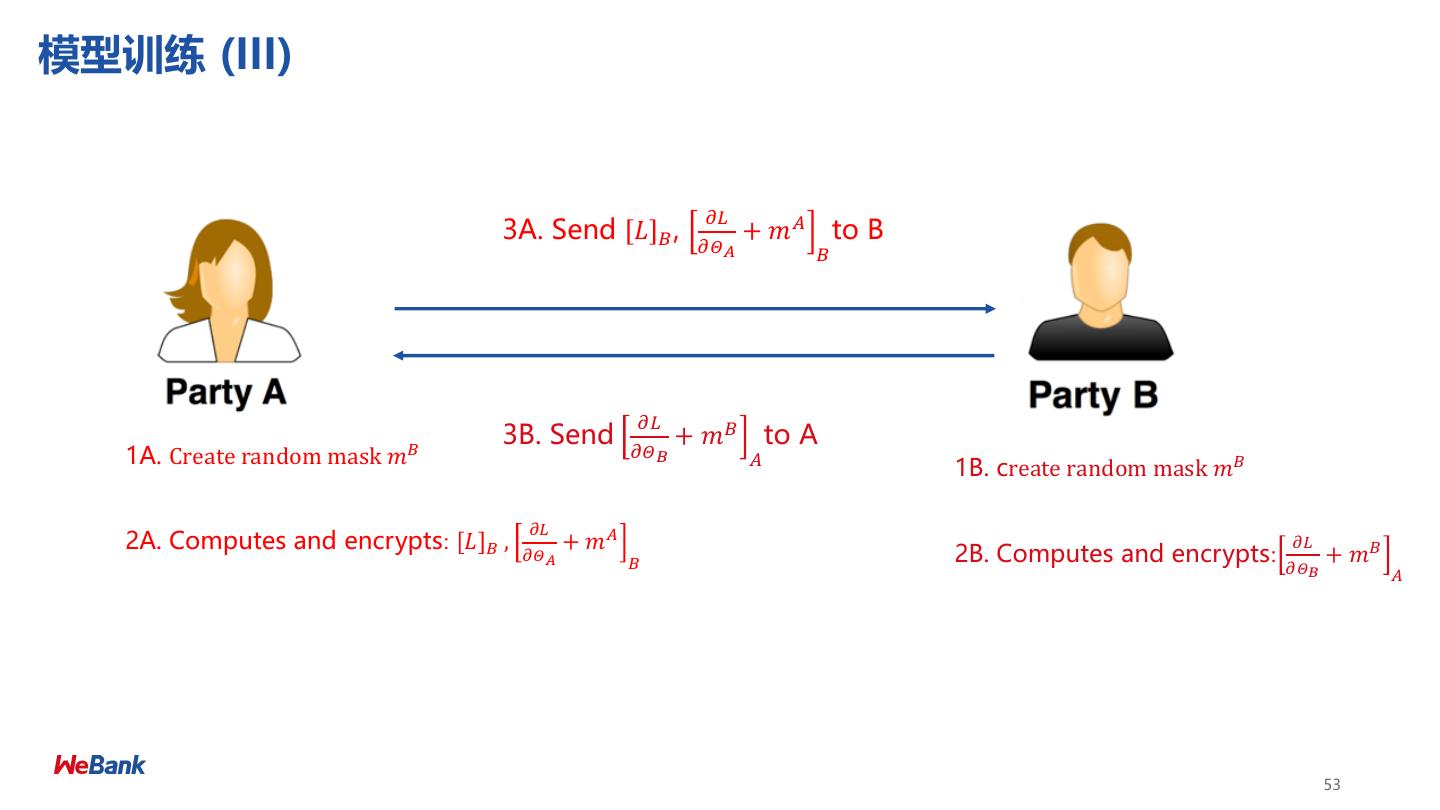
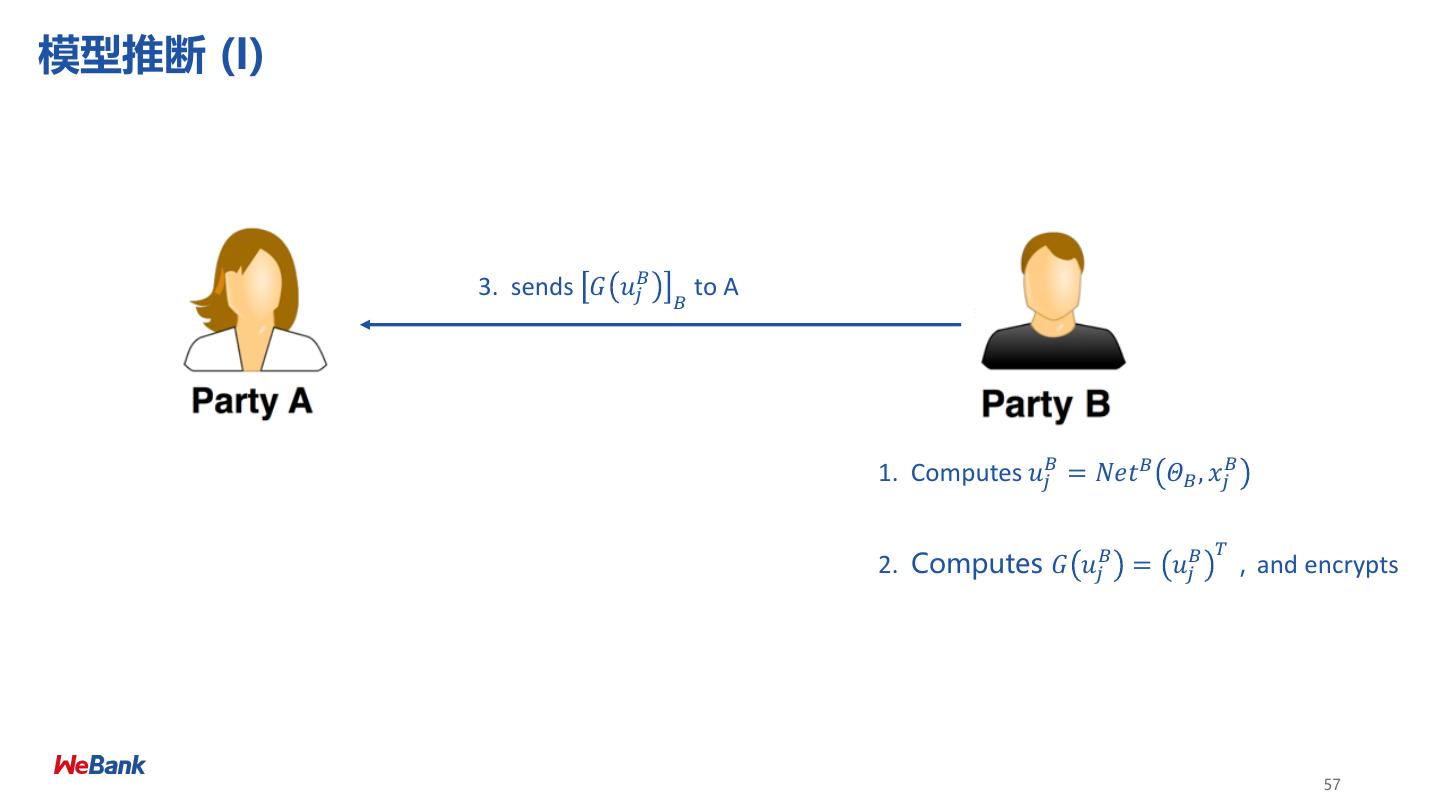
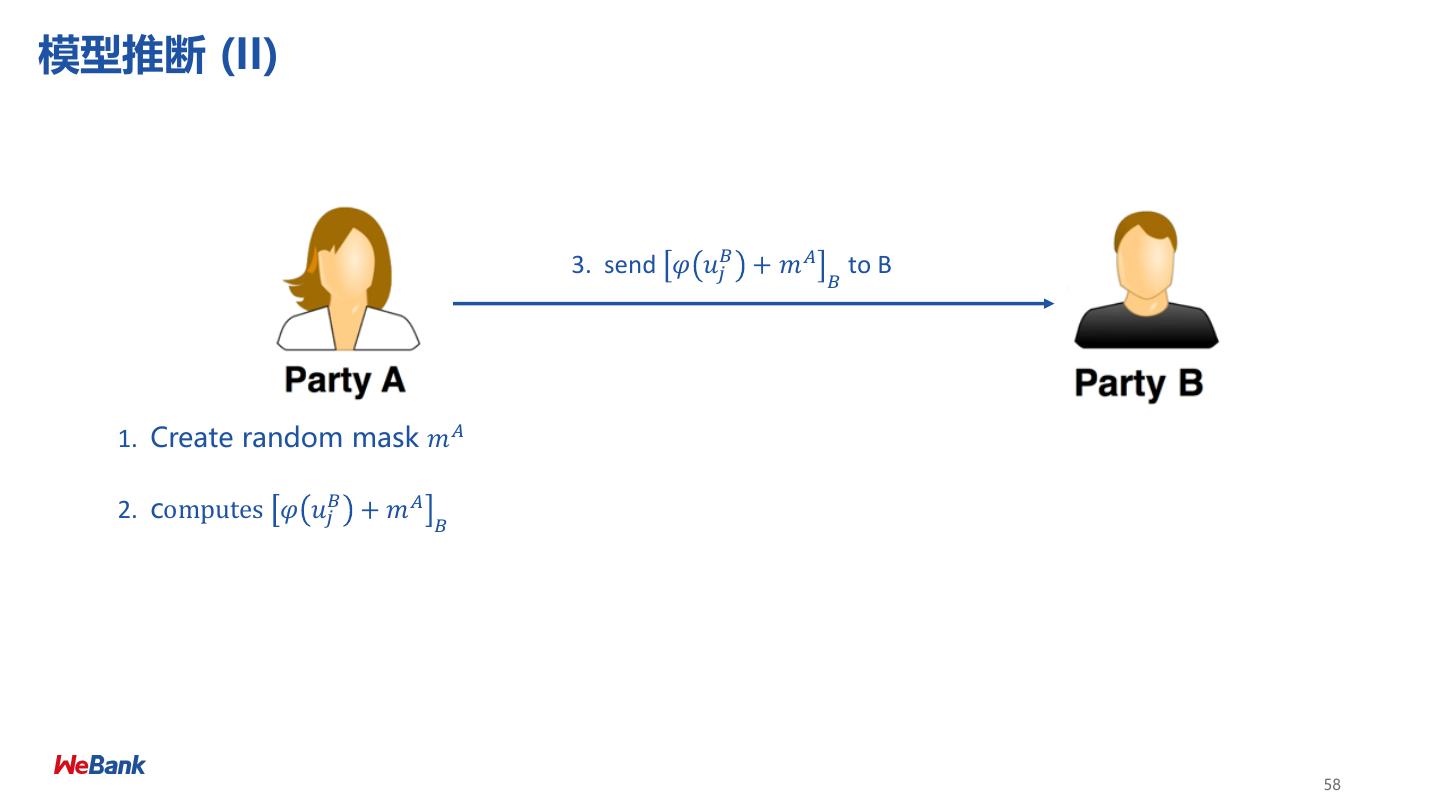
24 .联邦学习系统 Architecture of Vertical Federated Learning • Each Site Holds Own Data • Performance is LOSSLESS • Solution for Common Users 24
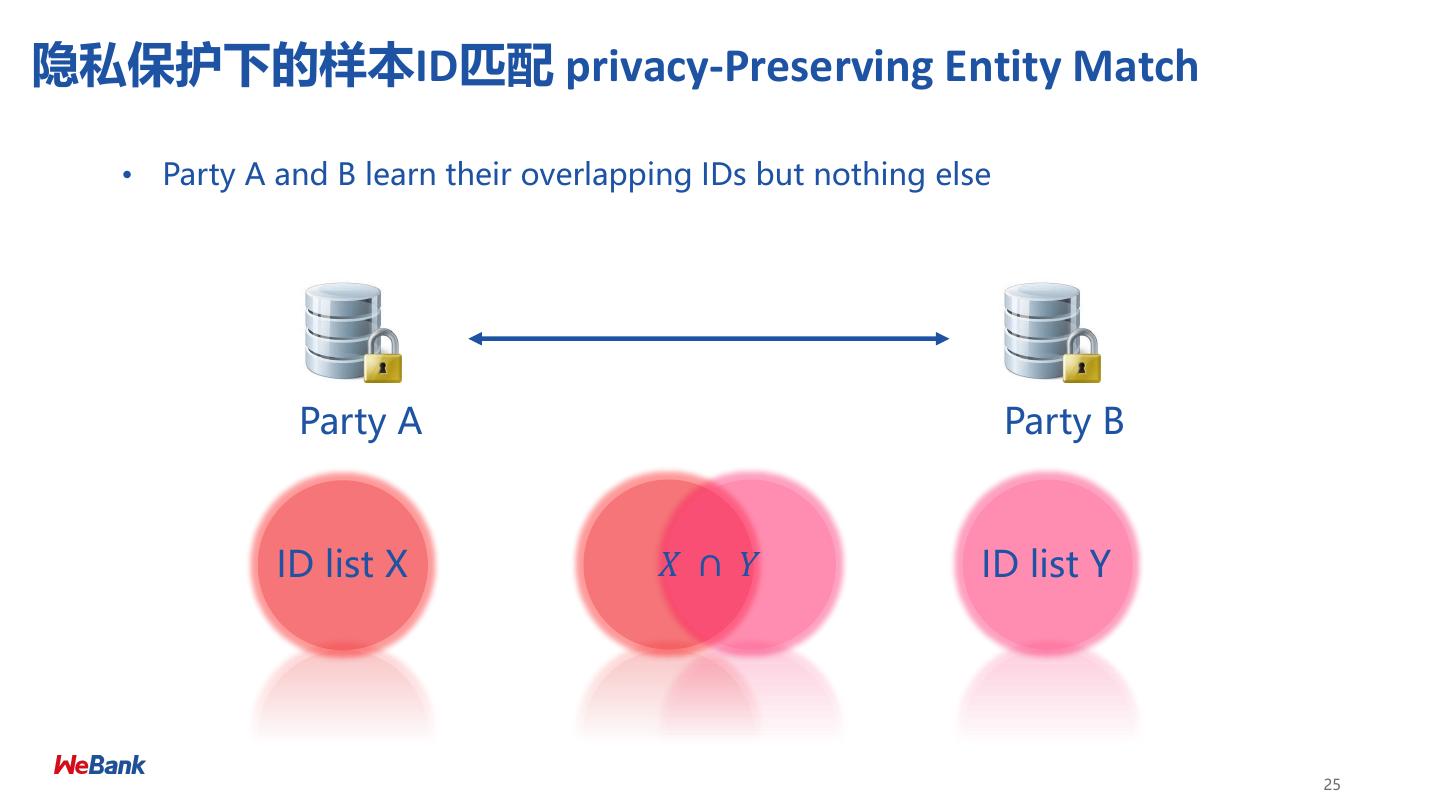
25 .隐私保护下的样本ID匹配 privacy-Preserving Entity Match • Party A and B learn their overlapping IDs but nothing else Party A Party B ID list X 𝑋 ∩ 𝑌 ID list Y 25
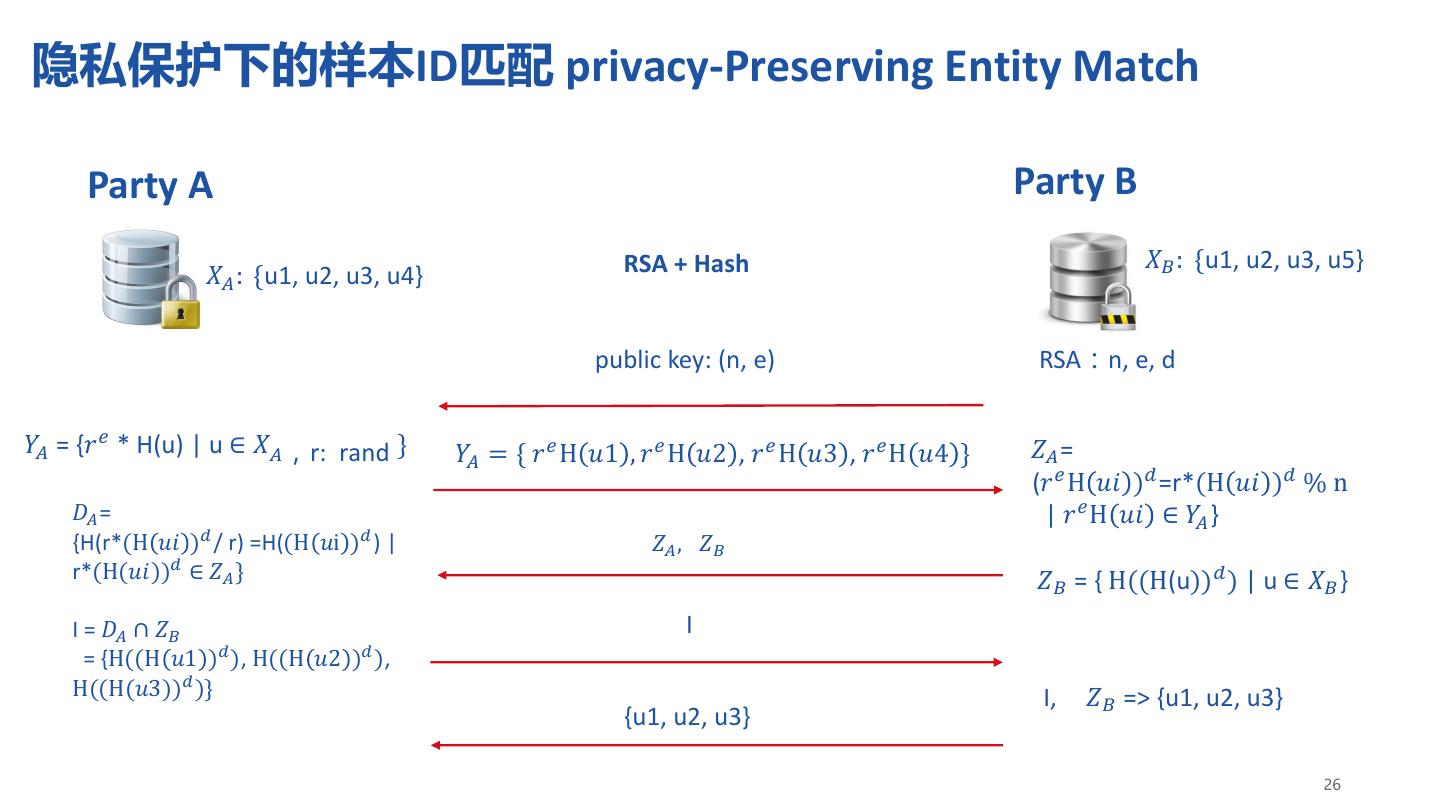
26 .隐私保护下的样本ID匹配 privacy-Preserving Entity Match Party A Party B RSA + Hash 𝑋𝐵 : {u1, u2, u3, u5} 𝑋𝐴 : {u1, u2, u3, u4} public key: (n, e) RSA:n, e, d 𝑌𝐴 = {𝑟 𝑒 * H(u) | u ∈ 𝑋𝐴,r: rand } 𝑌𝐴 = { 𝑟 𝑒 H 𝑢1 , 𝑟 𝑒 H 𝑢2 , 𝑟 𝑒 H 𝑢3 , 𝑟 𝑒 H 𝑢4 } 𝑍𝐴 = (𝑟 𝑒 H 𝑢𝑖 )𝑑 =r*(H 𝑢𝑖 )𝑑 % n 𝐷𝐴 = | 𝑟 𝑒 H 𝑢𝑖 ∈ 𝑌𝐴 } {H(r*(H 𝑢𝑖 )𝑑 / r) =H((H 𝑢i )𝑑 ) | 𝑍𝐴 , 𝑍𝐵 r*(H(𝑢𝑖))𝑑 ∈ 𝑍𝐴 } 𝑍𝐵 = { H((H(u))𝑑 ) | u ∈ 𝑋𝐵 } I = 𝐷𝐴 ∩ 𝑍𝐵 I = {H((H 𝑢1 )𝑑 ), H((H 𝑢2 )𝑑 ), H((H(𝑢3))𝑑 )} I, 𝑍𝐵 => {u1, u2, u3} {u1, u2, u3} 26
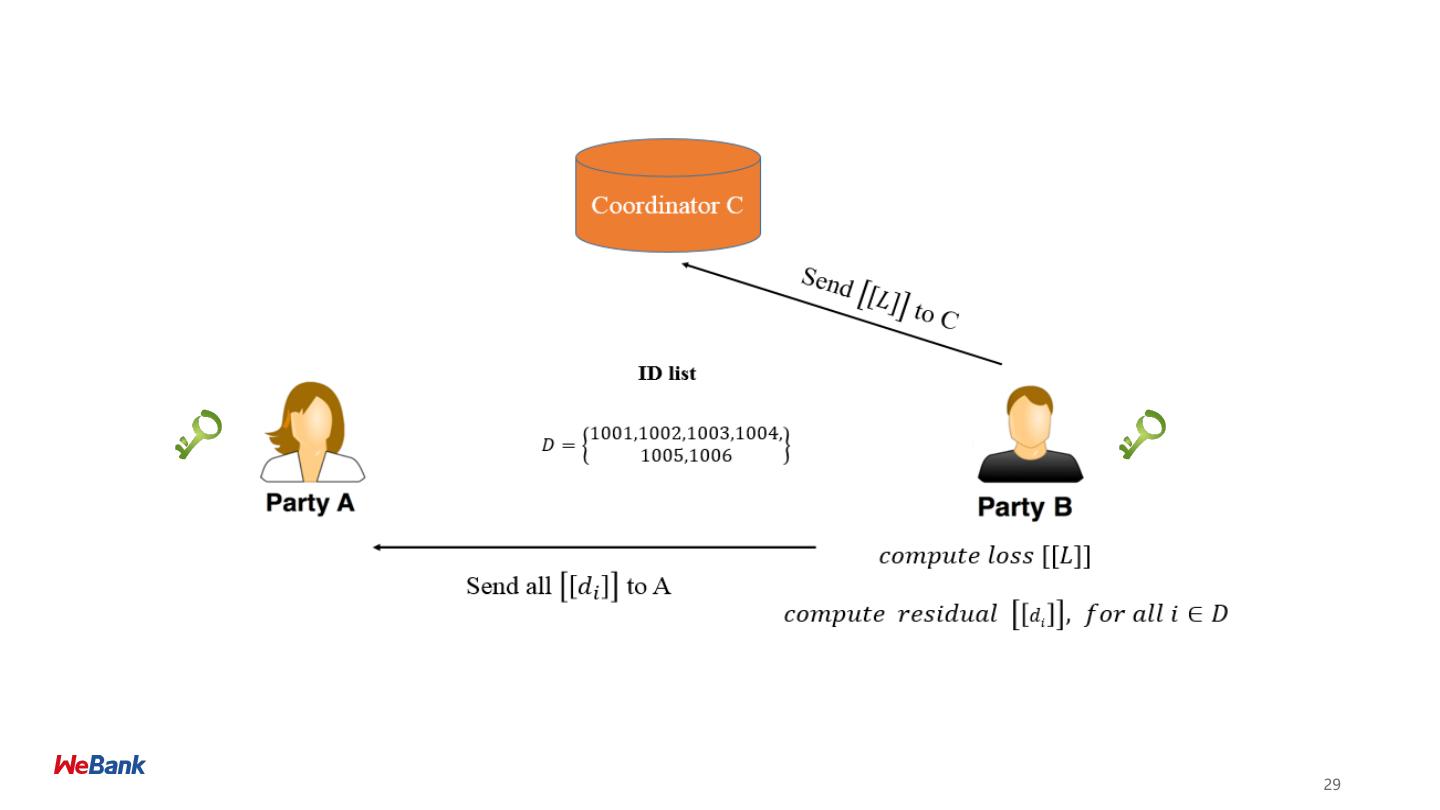
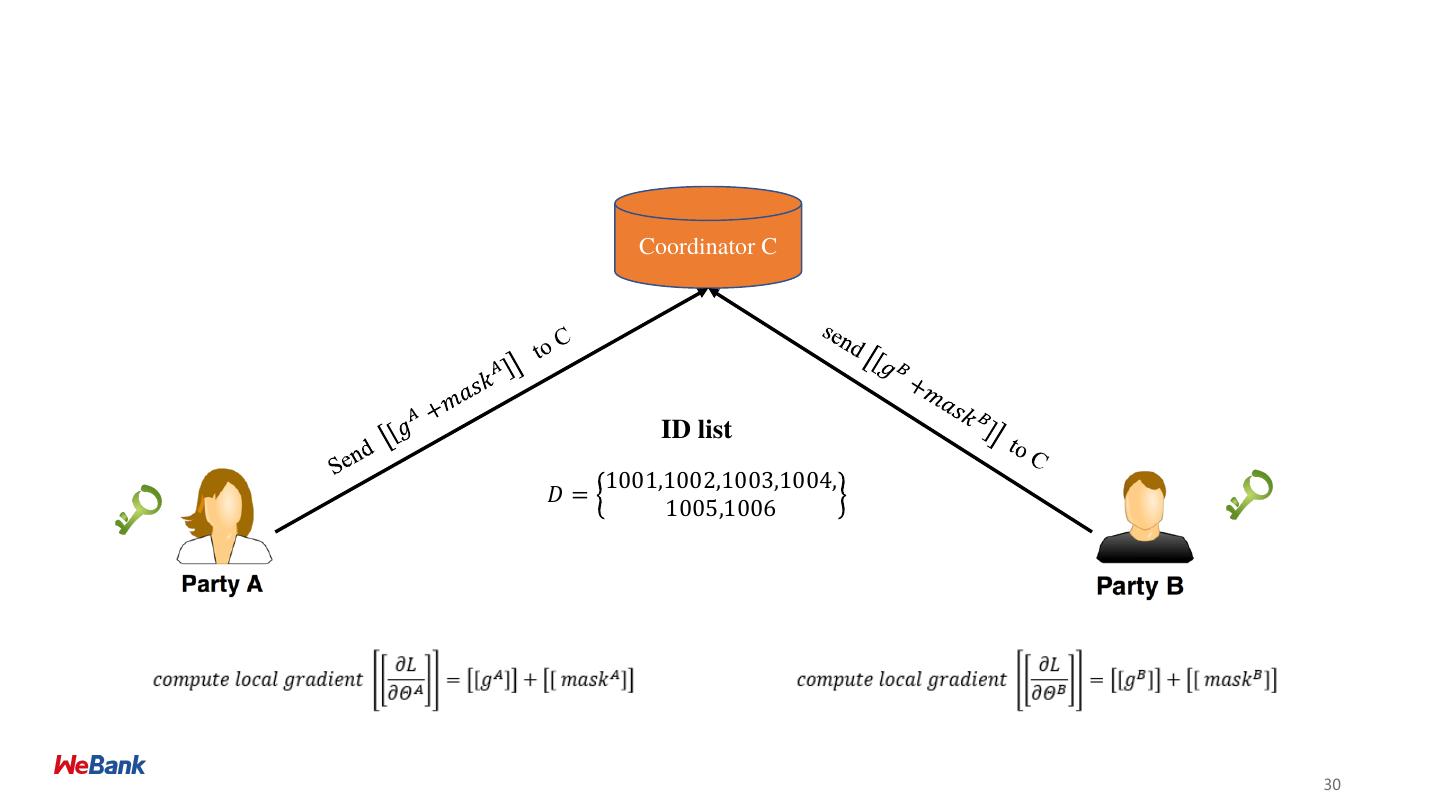
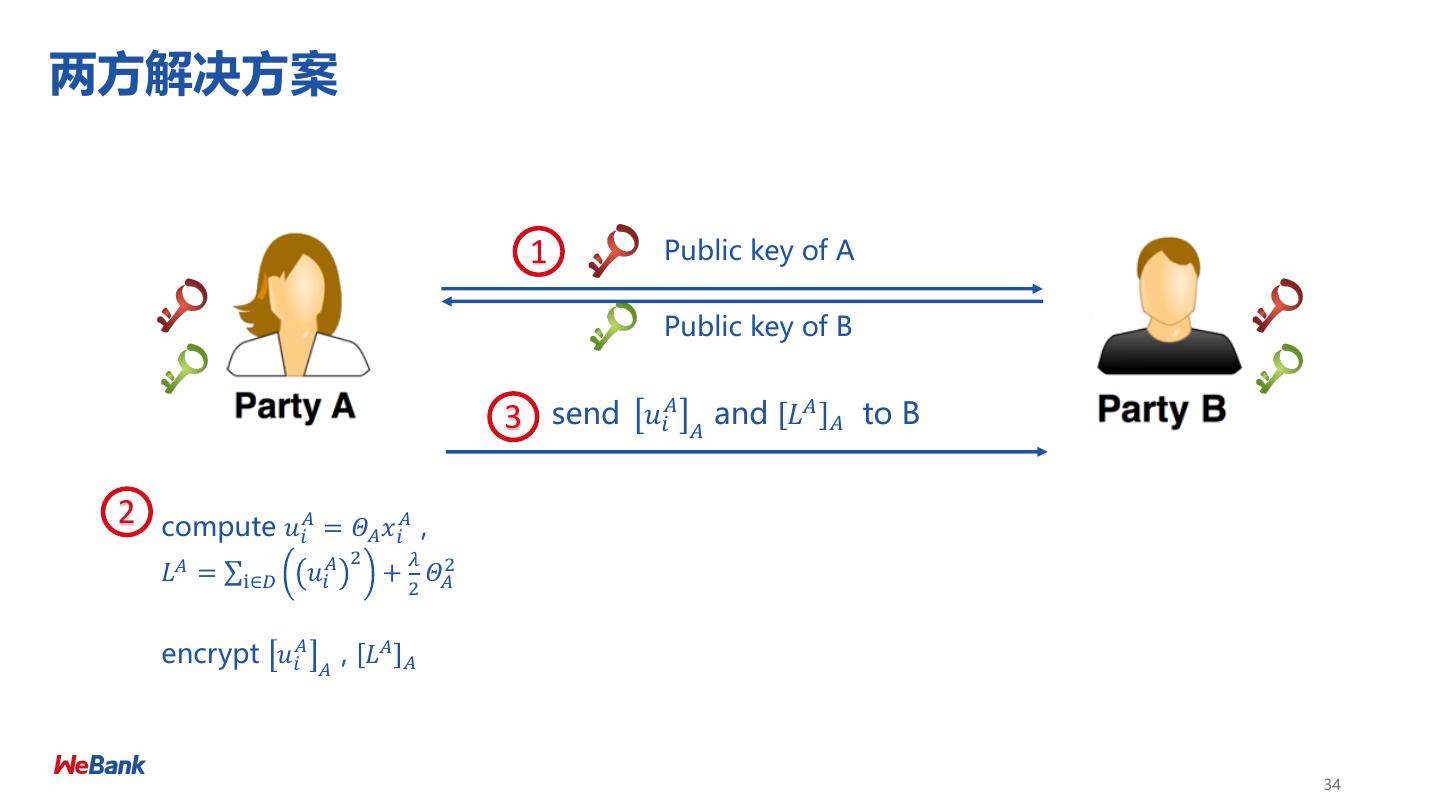
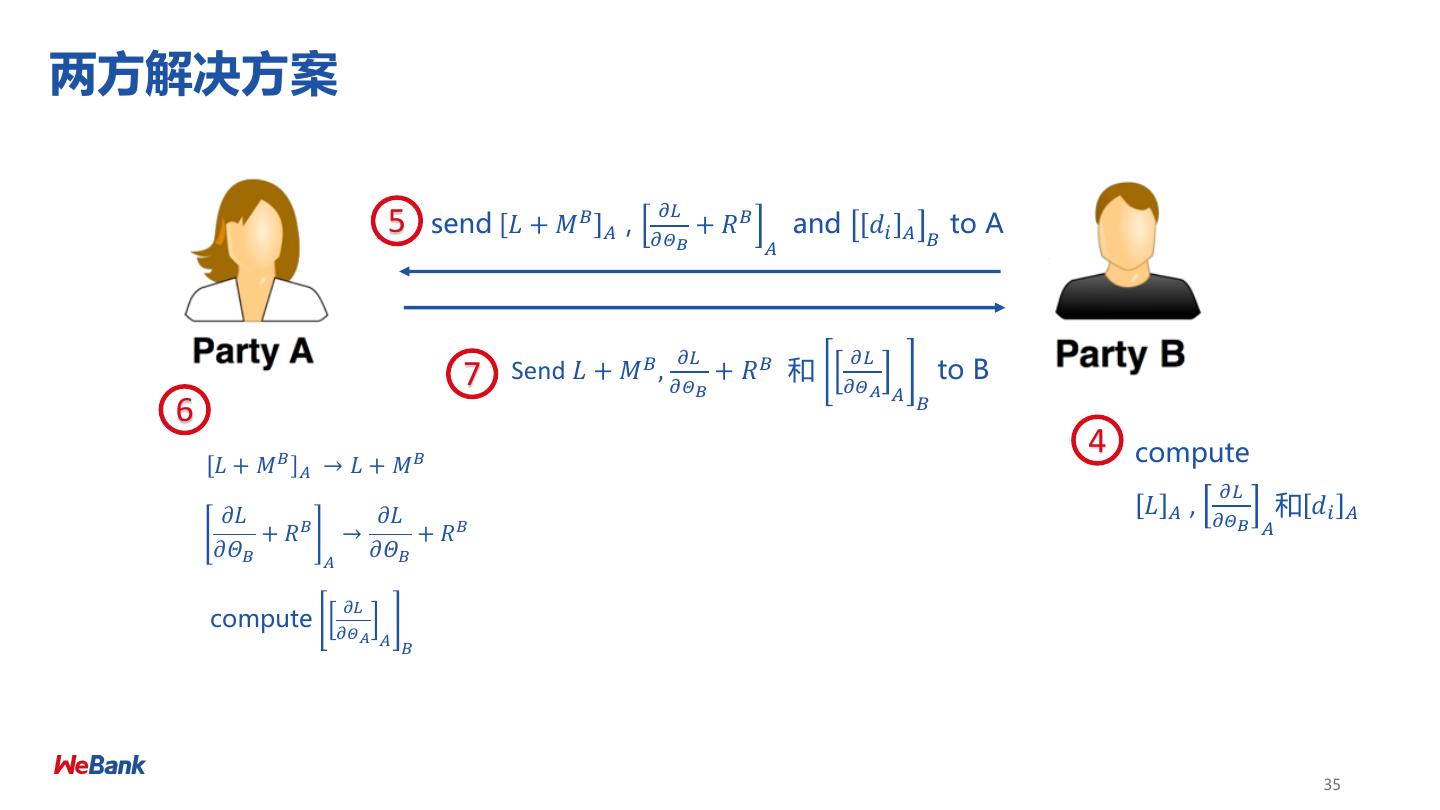
27 .隐私保护下的训练过程: Linear regression 27
28 .28
29 .29