绪论2--C++1信息的表示与存储

1 .绪论2：数据和程序的存储与表示 

2 . 内 容 （1）计算机的数字系统有哪些？ （2）如何进行不同进制数之间的转换？ （3）计算机中如何表示正、负数？ （4）计算机中如何表示整数和小数？ 

3 . 1、计算机的数字系统 基数为R的进制数：逢R进1 进制 基数 进位原则 基本符号 2进制 2 逢2进1 01 8进制 8 逢8进1 01234567 10进制 10 逢10进1 0123456789 16进制 16 逢16进1 0123456789ABCDEF 365进制 365 逢365进1 0 1 2 3 … 364 N进制 N 逢N进1 ? 所有的计算机都采用2进制的数字系统 优点：易于实现、运算简单、可靠性高、通用性强 

4 . 2、不同进制数之间的转换 任意R进制数X，其10进制值可表示为 权 10进制数 8844.43=8000 +800 +40 +4 +0.4 +0.03 =8x103+8x102+4x101+4x100+4x10-1+3x10-2 常用的转换形式有： （1）2进制、16进制←→10进制 （2）2进制←→16进制 

5 .2.A、2/16进制数→十进制的转换 各位数与权相成，积相加 (10001001.11)2=1x27+1x23+1x20+1x2-1+1x2-2 =(137.75)10 (0.2A)16=2x16-1+10x16-2 =(0.1640625)10 

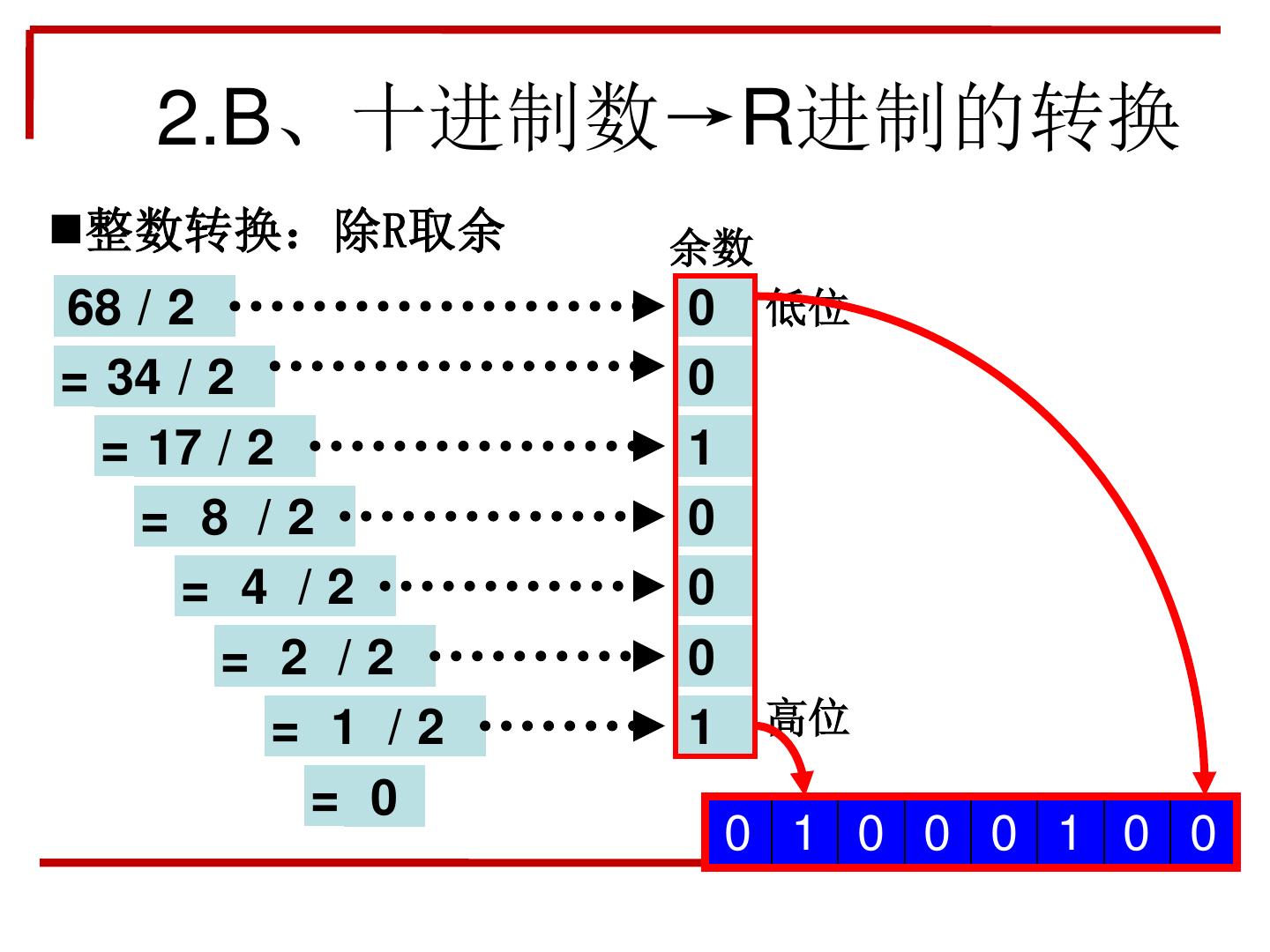
6 . 2.B、十进制数→R进制的转换 整数转换：除R取余 余数 68 / 2 0 低位 = 34 / 2 0 = 17 / 2 1 = 8 /2 0 = 4 /2 0 = 2 /2 0 = 1 /2 1 高位 = 0 0 1 0 0 0 1 0 0 

7 . 2.C、十进制数→R进制的转换 小数转换：乘R取整 高位 0.3125 x 2 = 0.625 例：10进制整0.3125 0.625 x 2 = 1.25 0.25 x 2 = 0.5 0.5 x 2 = 1.0 0 1 0 1 

8 . 2.D、16进制←→2进制  1:4（每位16进制数相当于4位2进制数） (1011010.10)2=(0101 1010 .1000)2=(5A.8)16 (F7)16＝(1111 0111)2＝(11110111)2 

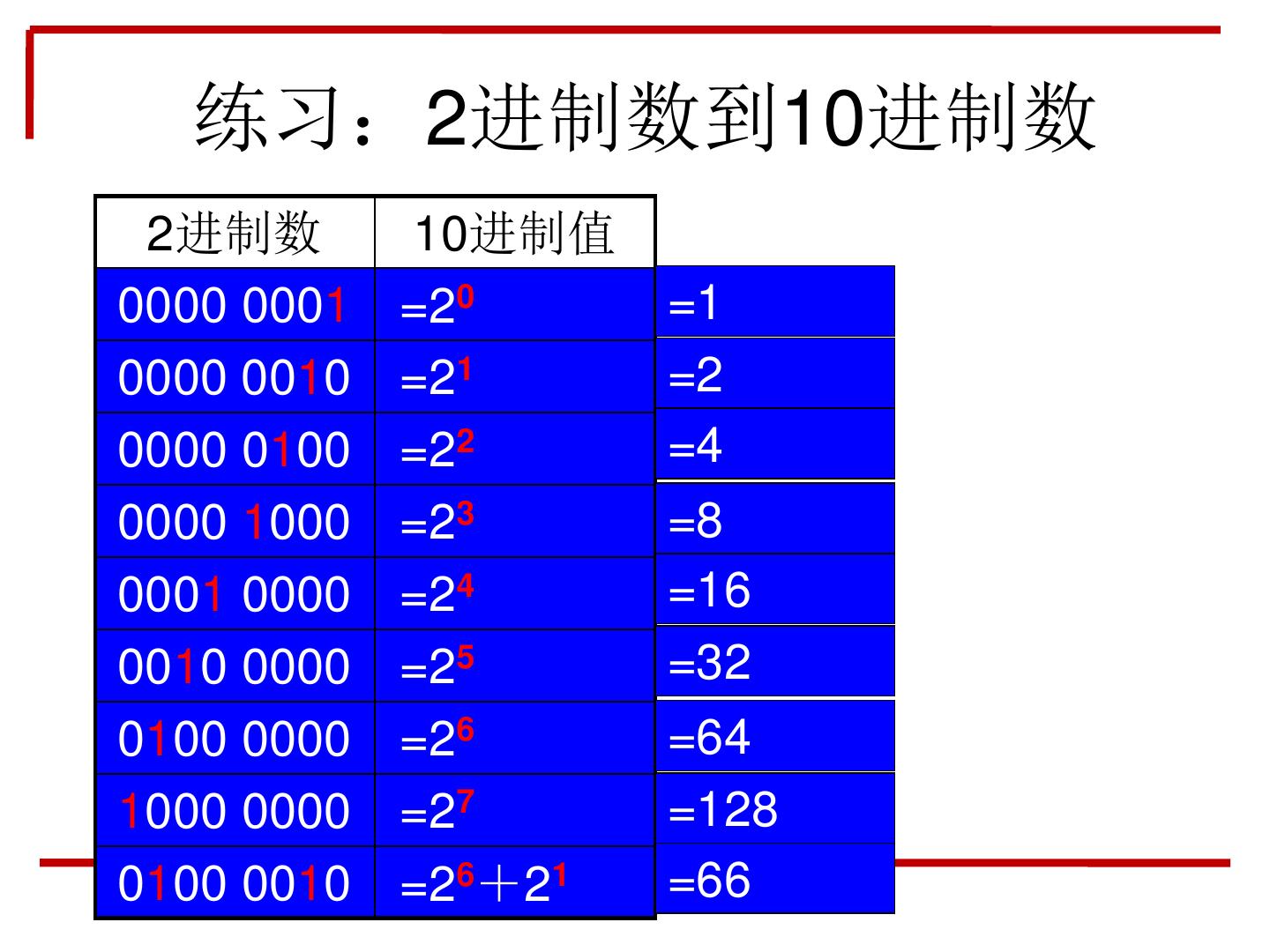
9 . 练习：2进制数到10进制数 2进制数 10进制值 0000 0001 =20 =1 =? 0000 0010 =21 =? =2 0000 0100 =22 =? =4 0000 1000 =23 =8 =? 0001 0000 =24 =? =16 0010 0000 =25 =? =32 0100 0000 =26 =64 =? 1000 0000 =27 =? =128 0100 0010 =26＋21 =? =66 

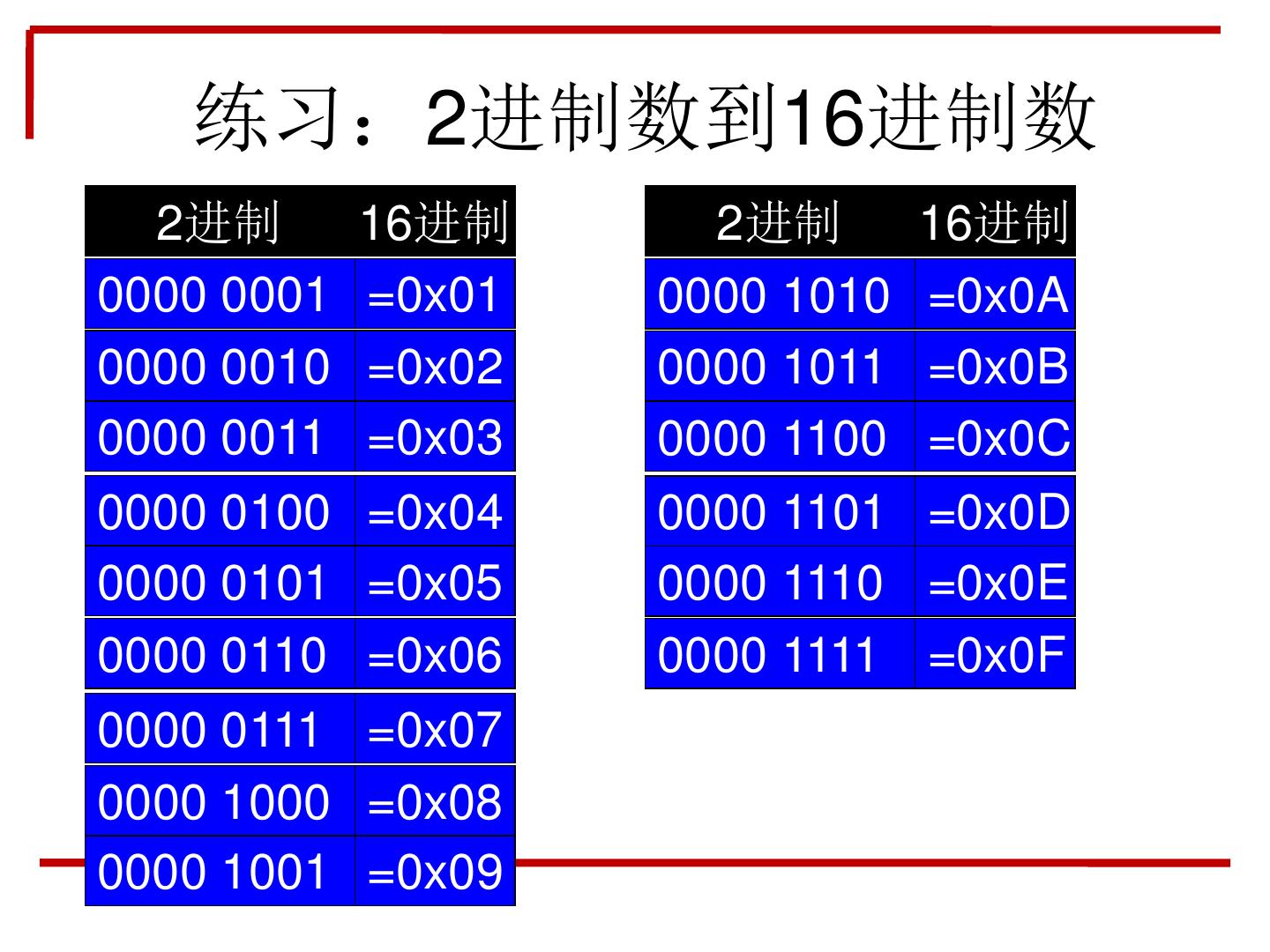
10 . 练习：2进制数到16进制数 2进制 16进制 2进制 16进制 0000 0001 =0x01 0000 1010 =0x0A 0000 0010 =0x02 0000 1011 =0x0B 0000 0011 =0x03 0000 1100 =0x0C 0000 0100 =0x04 0000 1101 =0x0D 0000 0101 =0x05 0000 1110 =0x0E 0000 0110 =0x06 0000 1111 =0x0F 0000 0111 =0x07 0000 1000 =0x08 0000 1001 =0x09 

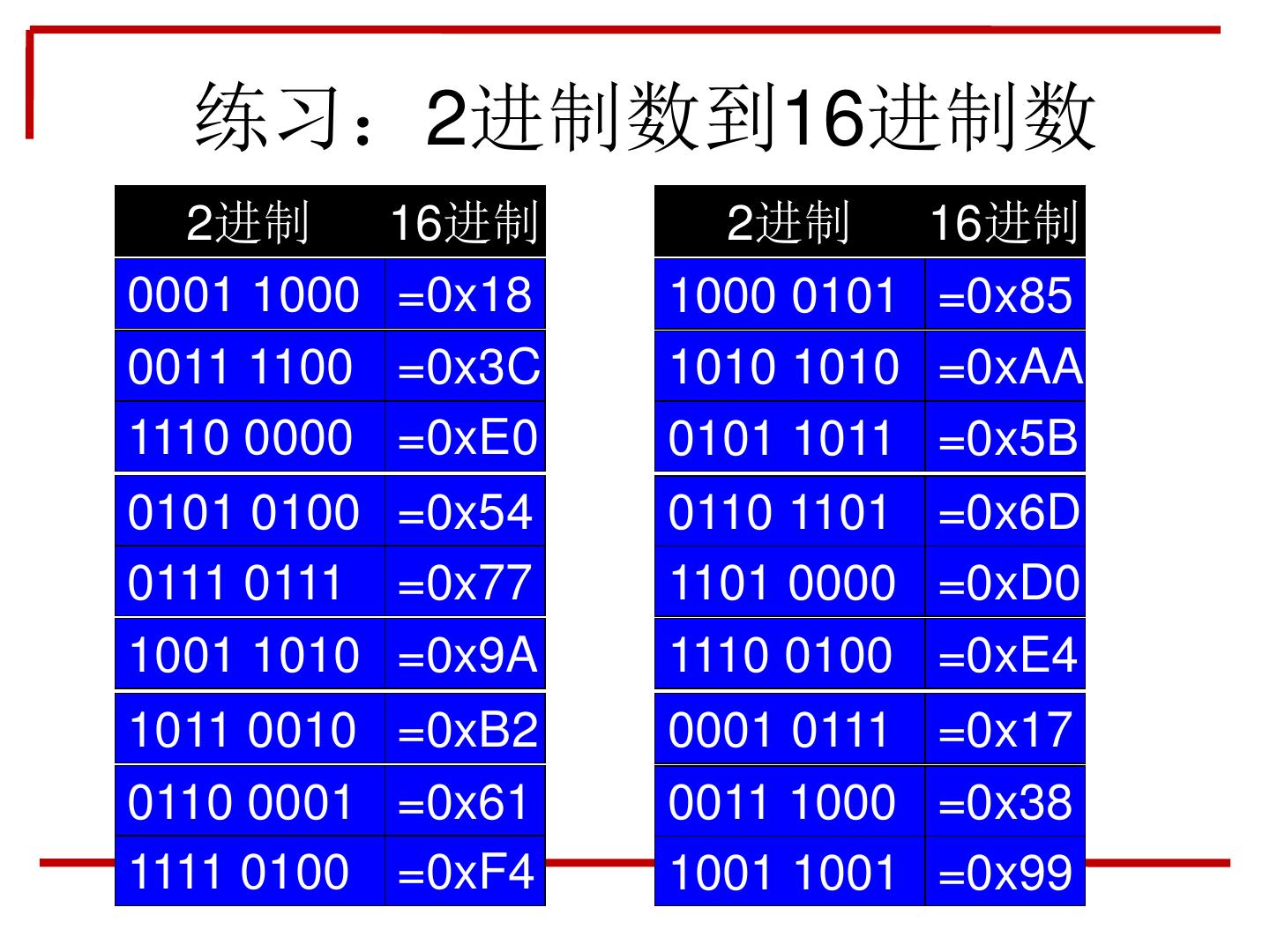
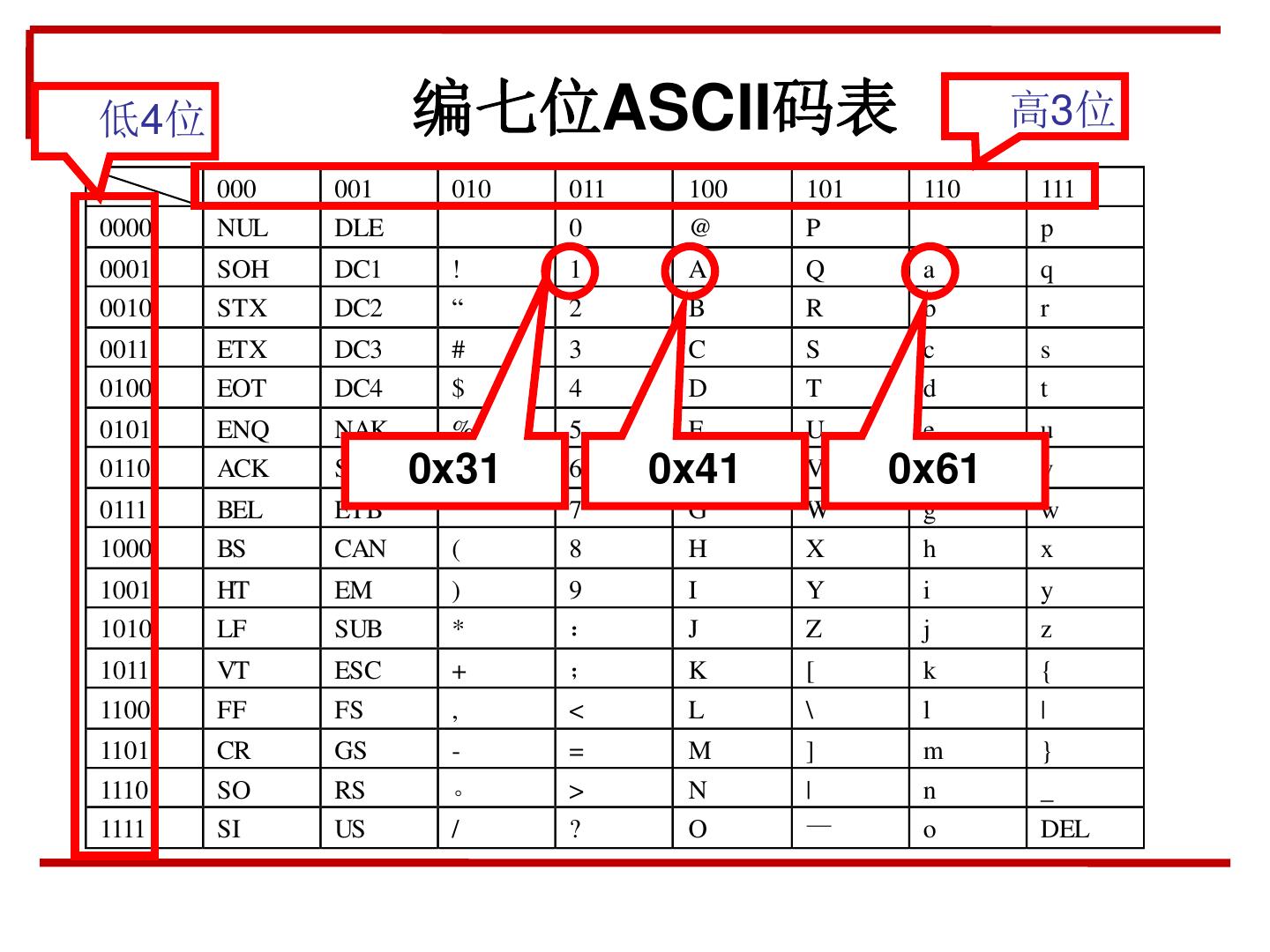
11 . 练习：2进制数到16进制数 2进制 16进制 2进制 16进制 0001 1000 =0x18 1000 0101 =0x85 0011 1100 =0x3C 1010 1010 =0xAA 1110 0000 =0xE0 0101 1011 =0x5B 0101 0100 =0x54 0110 1101 =0x6D 0111 0111 =0x77 1101 0000 =0xD0 1001 1010 =0x9A 1110 0100 =0xE4 1011 0010 =0xB2 0001 0111 =0x17 0110 0001 =0x61 0011 1000 =0x38 1111 0100 =0xF4 1001 1001 =0x99 

12 .• 3.A 数据的不同理解 

13 .• 数据在存储器中的表示 

14 .• 数据在存储器中的表示 

15 .• 3.B -1如何表示 

16 .• -1的表示 

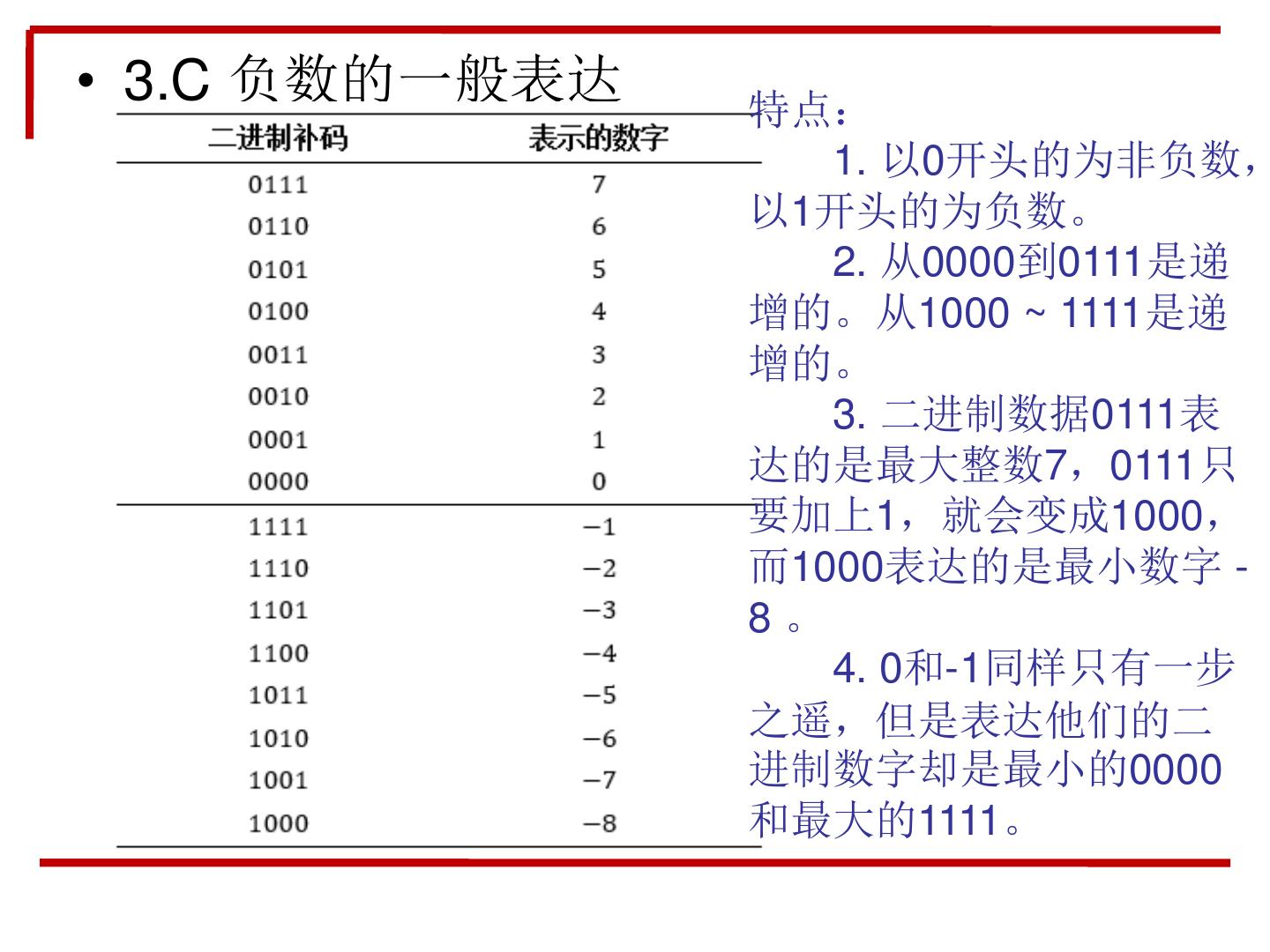
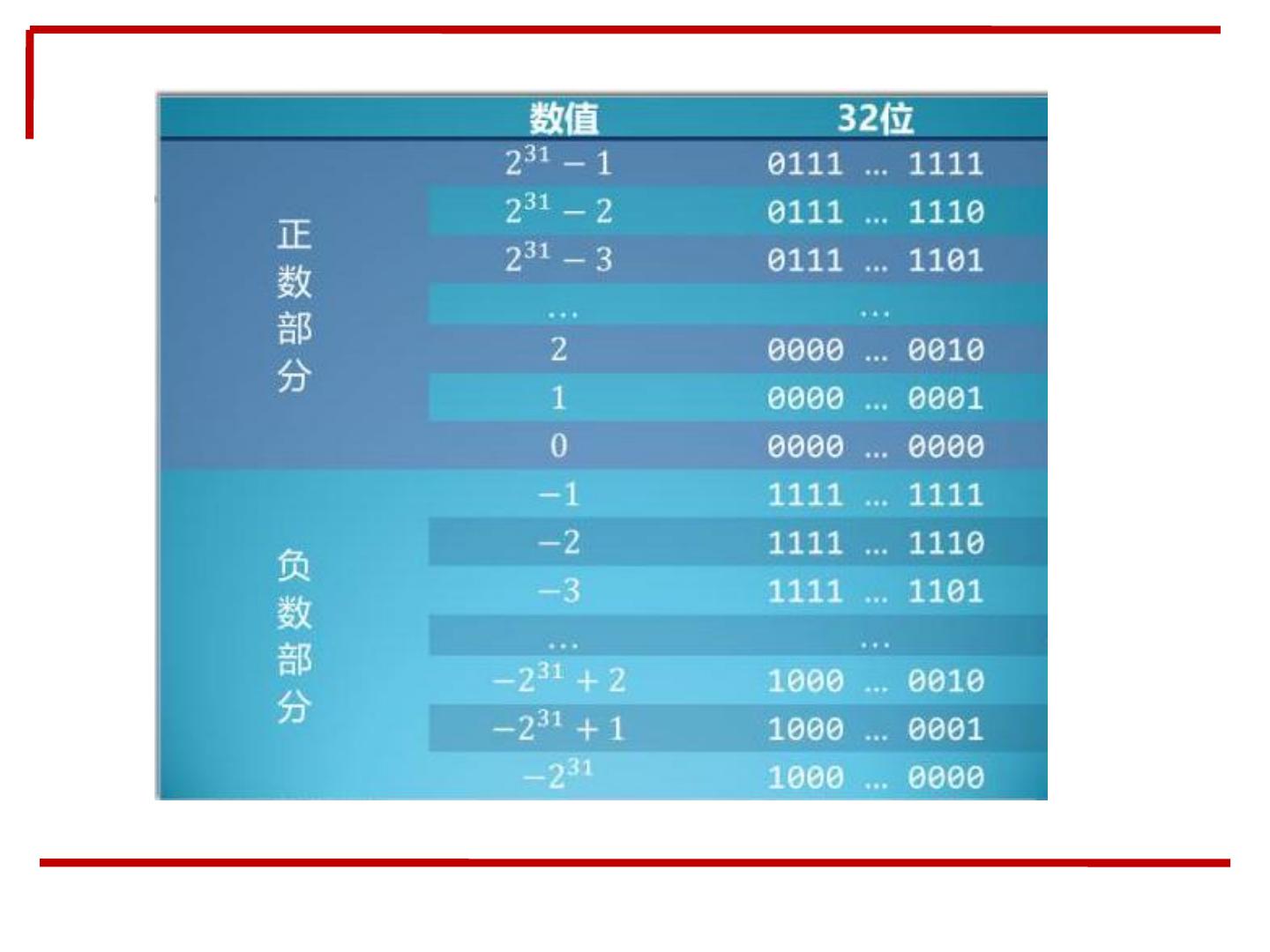
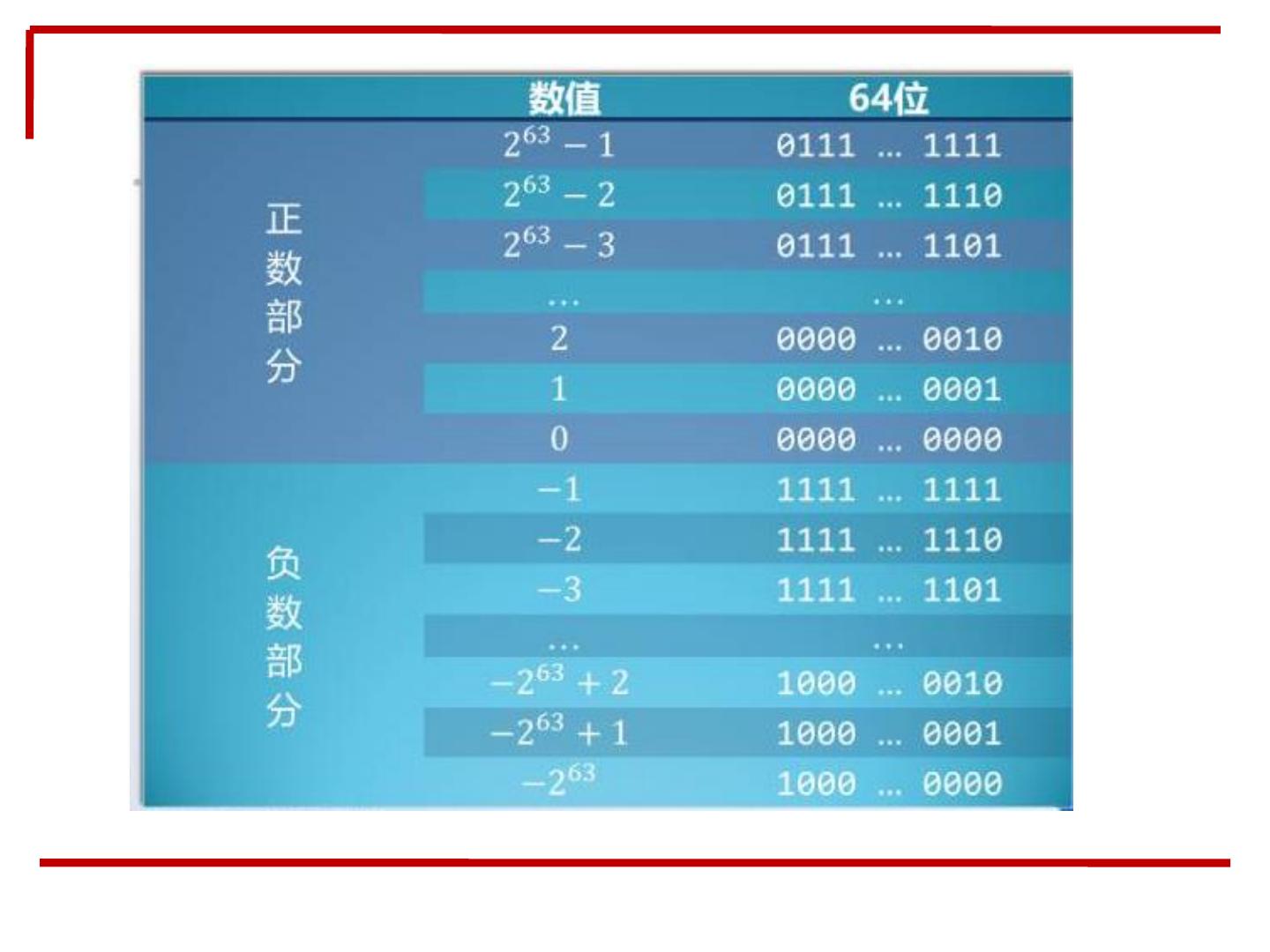
17 .• 3.C 负数的一般表达 特点： 1. 以0开头的为非负数， 以1开头的为负数。 2. 从0000到0111是递 增的。从1000 ~ 1111是递 增的。 3. 二进制数据0111表 达的是最大整数7，0111只 要加上1，就会变成1000， 而1000表达的是最小数字 - 8。 4. 0和-1同样只有一步 之遥，但是表达他们的二 进制数字却是最小的0000 和最大的1111。 

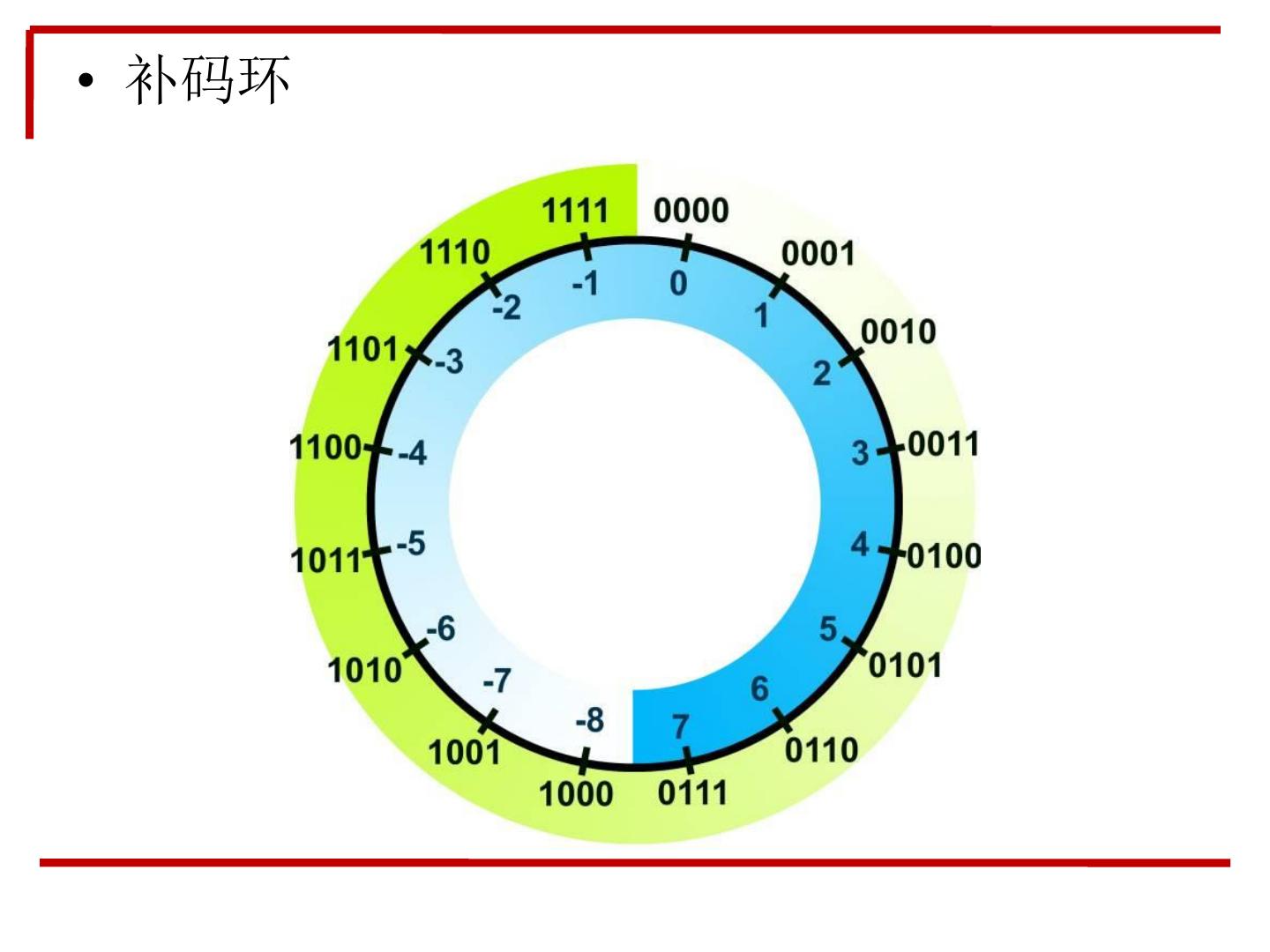
18 .• 补码环 

19 .

20 .

21 .

22 .

23 .

24 .

25 .

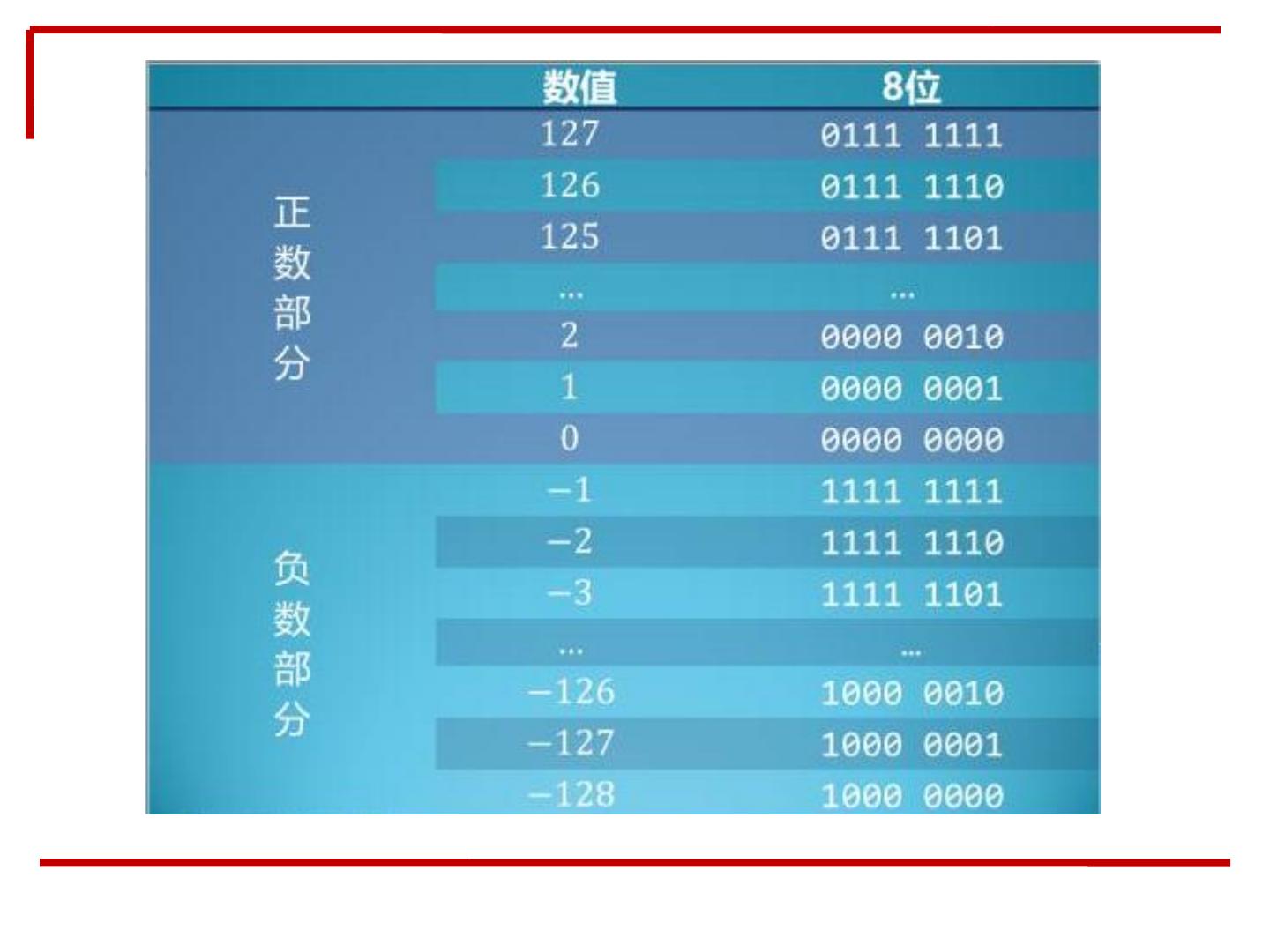
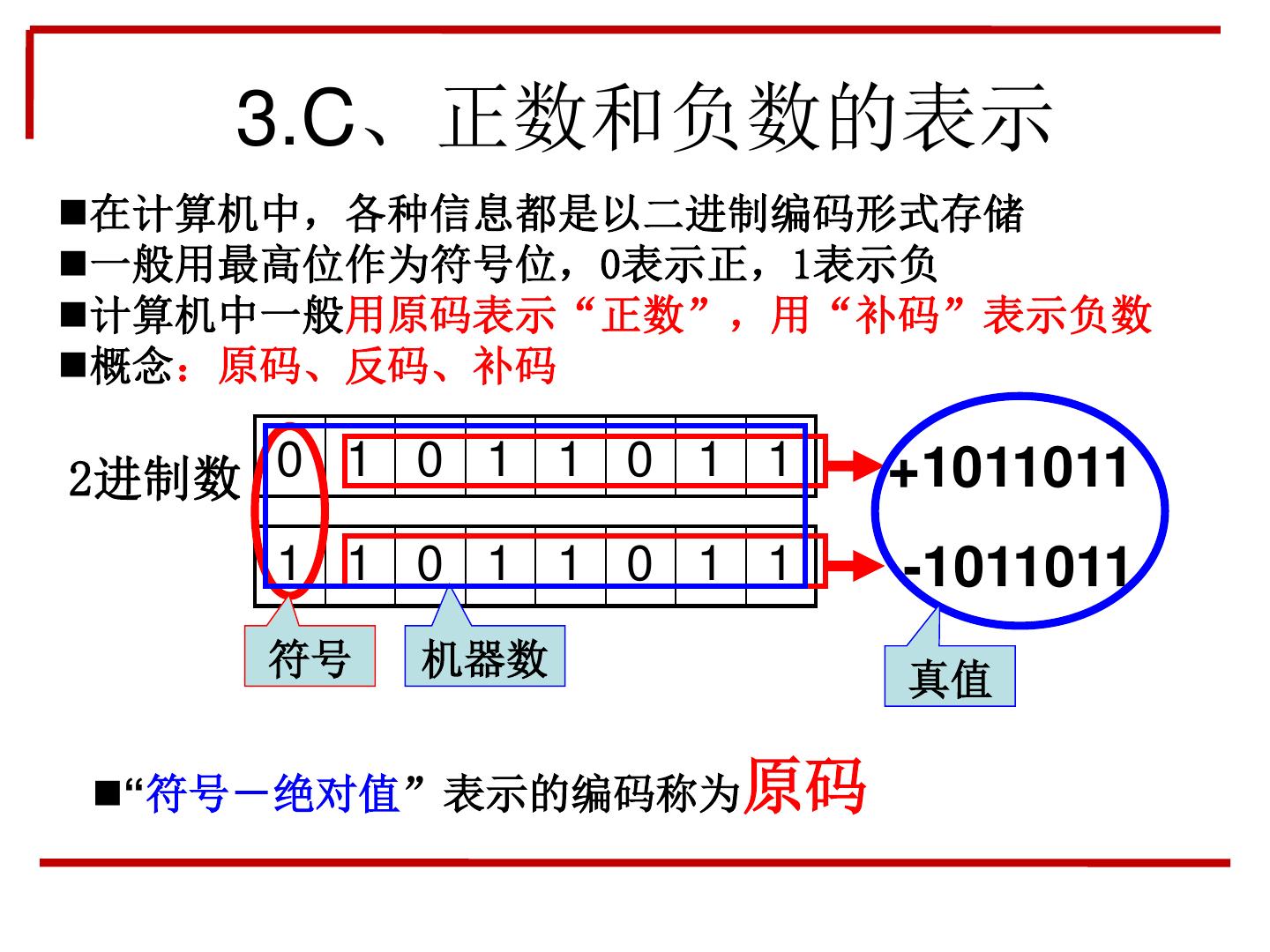
26 . 3.C、正数和负数的表示 在计算机中，各种信息都是以二进制编码形式存储 一般用最高位作为符号位，0表示正，1表示负 计算机中一般用原码表示“正数”，用“补码”表示负数 概念：原码、反码、补码 2进制数 0 1 0 1 1 0 1 1 +1011011 1 1 0 1 1 0 1 1 -1011011 符号 机器数 真值 “符号－绝对值”表示的编码称为原码 

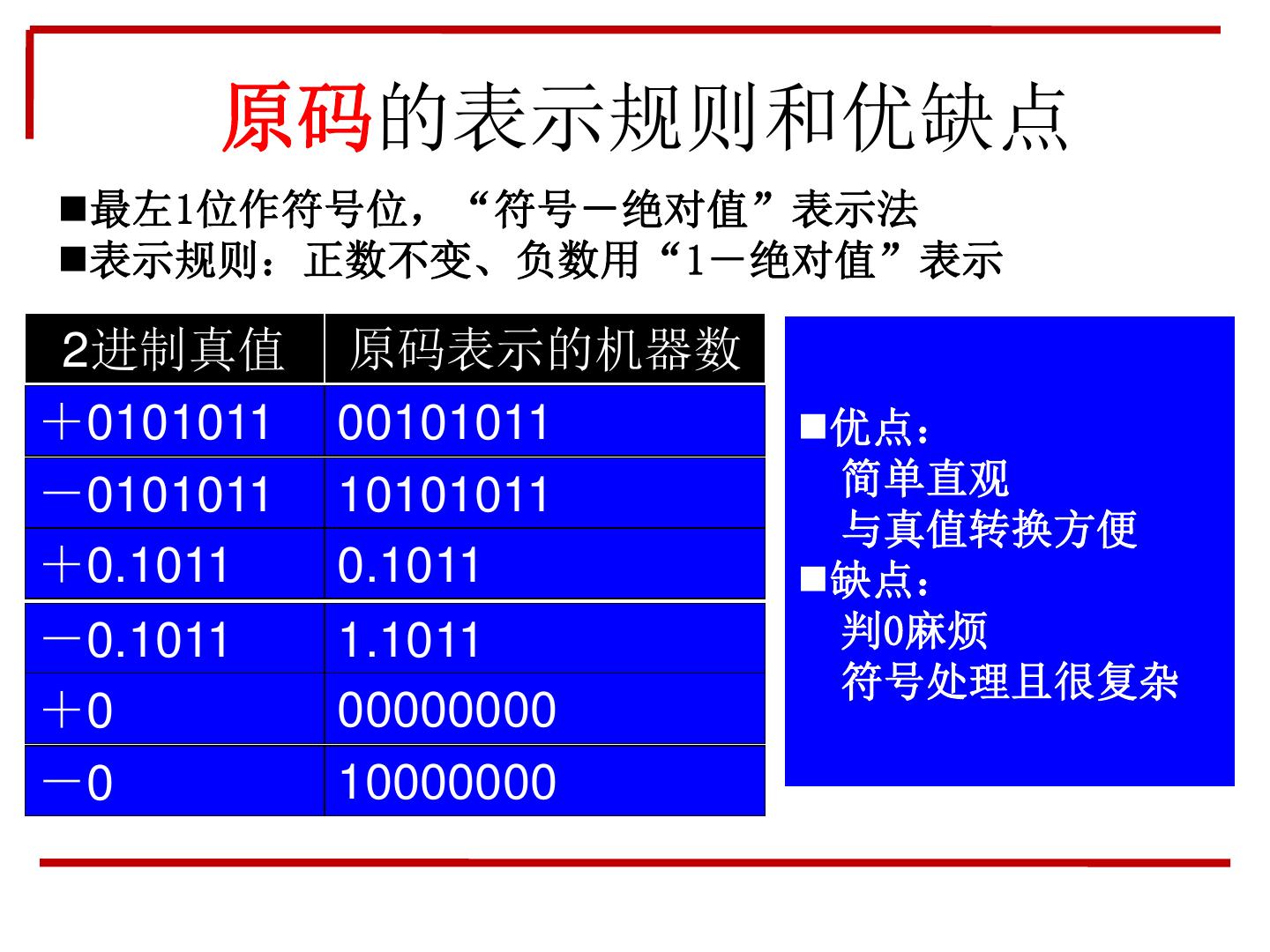
27 . 原码的表示规则和优缺点 最左1位作符号位，“符号－绝对值”表示法 表示规则：正数不变、负数用“1－绝对值”表示 2进制真值 原码表示的机器数 ＋0101011 00101011 优点： －0101011 10101011 简单直观 与真值转换方便 ＋0.1011 0.1011 缺点： －0.1011 1.1011 判0麻烦 符号处理且很复杂 ＋0 00000000 －0 10000000 

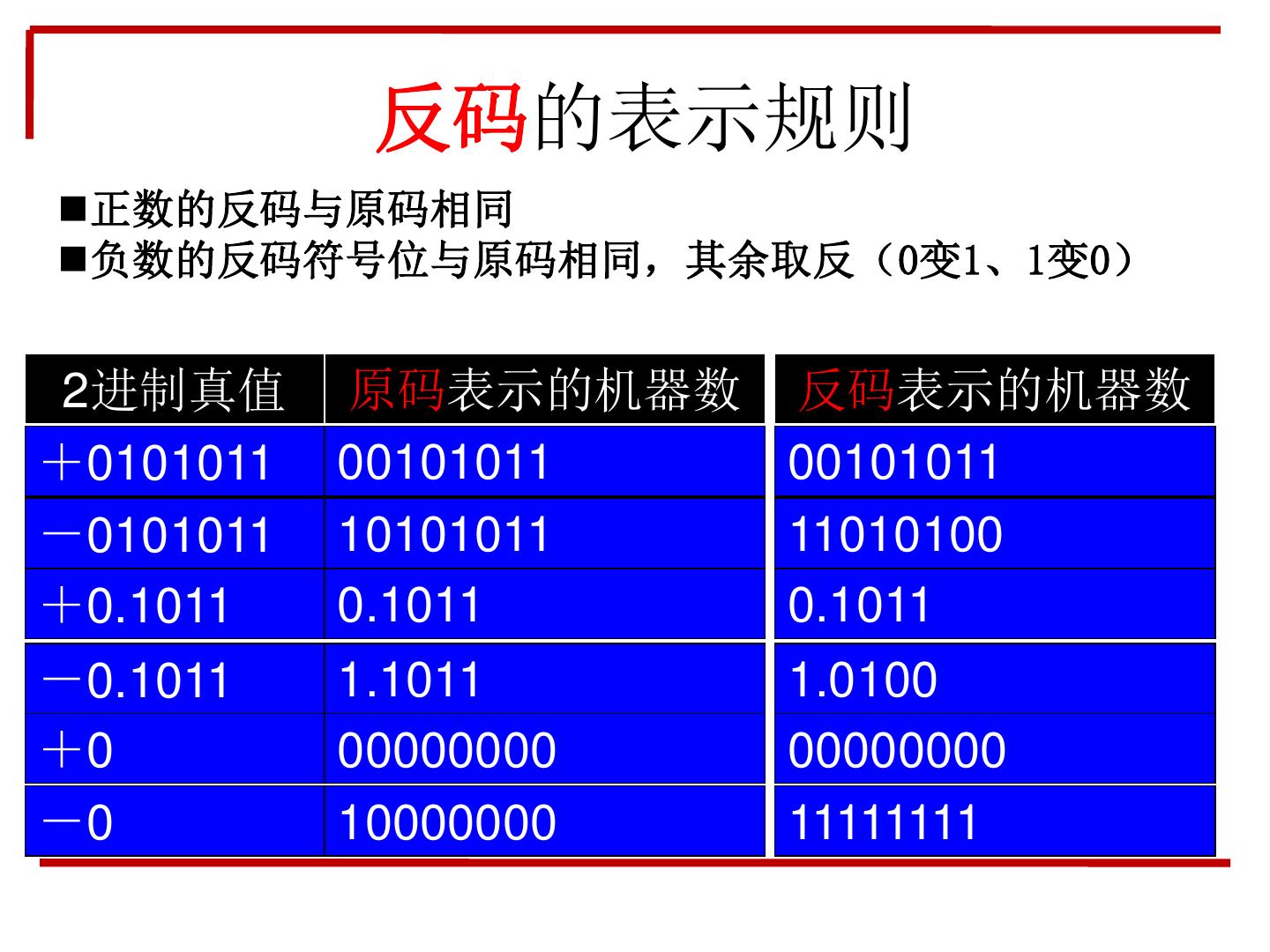
28 . 反码的表示规则 正数的反码与原码相同 负数的反码符号位与原码相同，其余取反（0变1、1变0） 2进制真值 原码表示的机器数 反码表示的机器数 ＋0101011 00101011 00101011 －0101011 10101011 11010100 ＋0.1011 0.1011 0.1011 －0.1011 1.1011 1.0100 ＋0 00000000 00000000 －0 10000000 11111111 

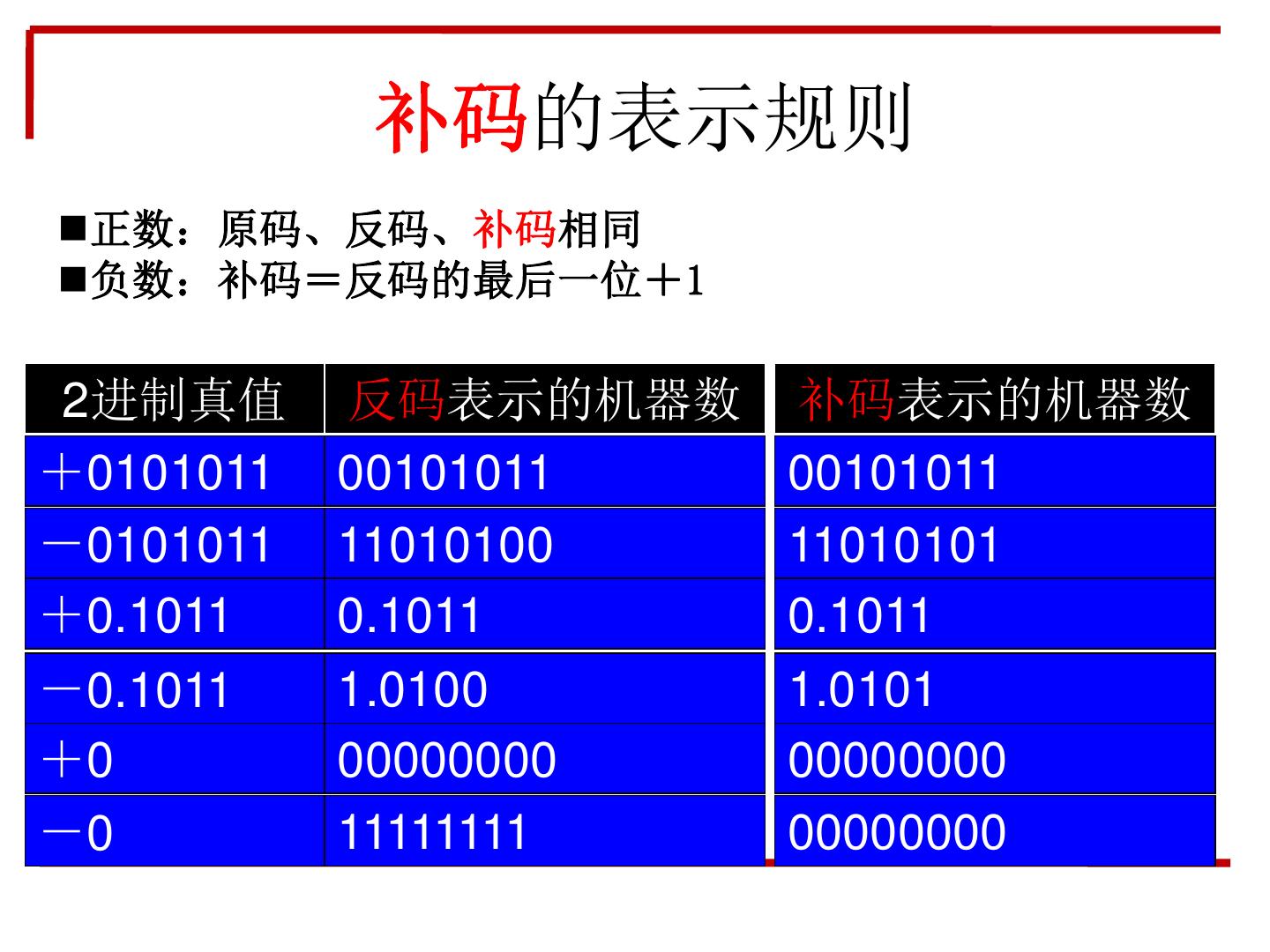
29 . 补码的表示规则 正数：原码、反码、补码相同 负数：补码＝反码的最后一位＋1 2进制真值 反码表示的机器数 补码表示的机器数 ＋0101011 00101011 00101011 －0101011 11010100 11010101 ＋0.1011 0.1011 0.1011 －0.1011 1.0100 1.0101 ＋0 00000000 00000000 －0 11111111 00000000