1 .Computer vision: models, learning and inference Chapter 18 Models for style and identity

2 .Identity and Style 2 2 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince Identity differs, but images similar Identity same, but images quite different

3 .Structure 3 3 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince Factor analysis review Subspace identity model Linear discriminant analysis Non-linear models Asymmetric bilinear model Symmetric bilinear model Applications

4 .Factor analysis review 4 4 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince Generative equation: Probabilistic form: Marginal density:

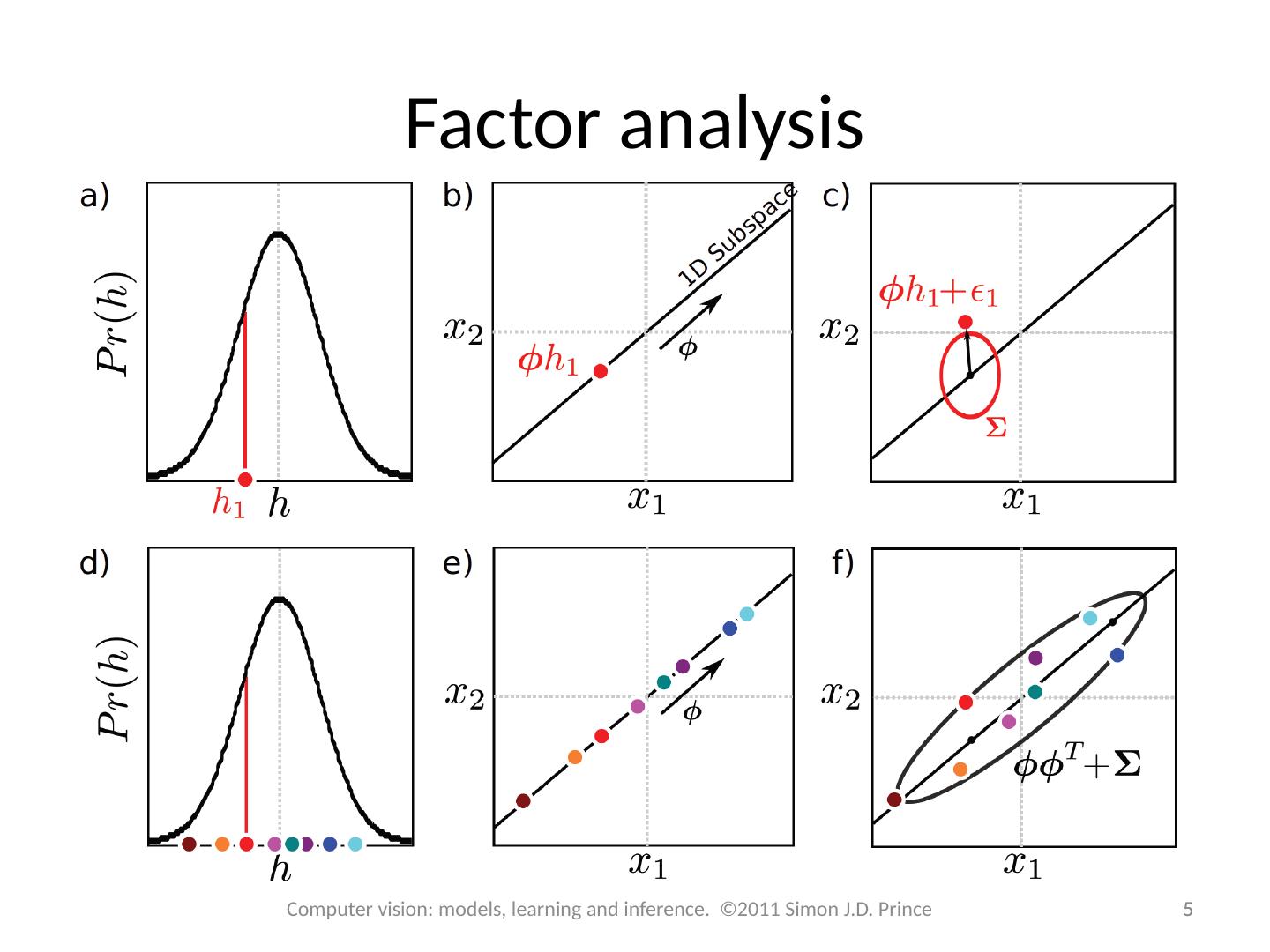
5 .Factor analysis 5 5 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince

6 .Factor analysis review 6 6 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince E-Step: M-Step:

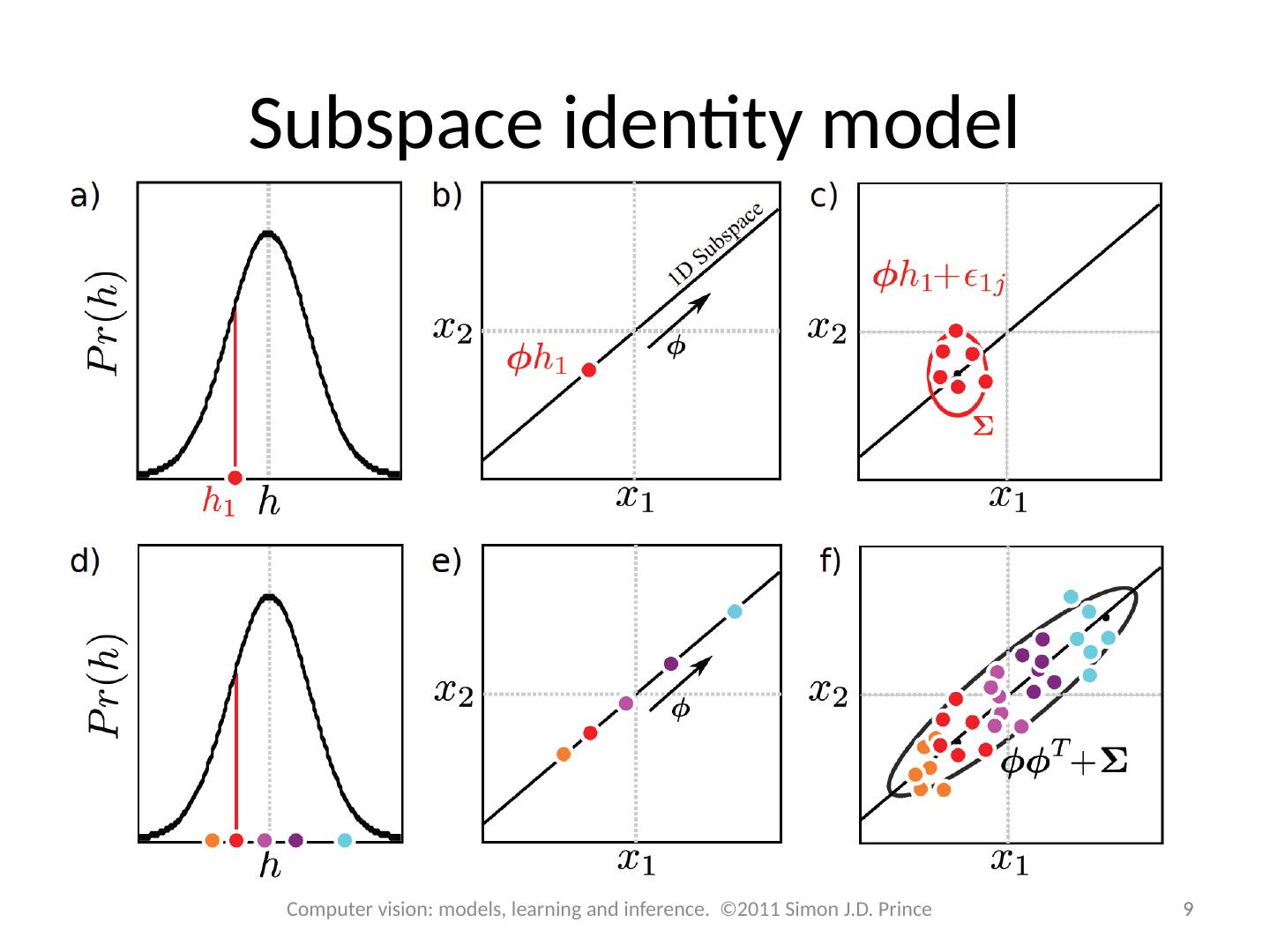
7 .Factor analysis vs. Identity model 7 7 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince Each color is a different identity multiple images lie in similar part of subspace

8 .Subspace identity model 8 8 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince Generative equation: Probabilistic form: Marginal density:

9 .Subspace identity model 9 9 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince

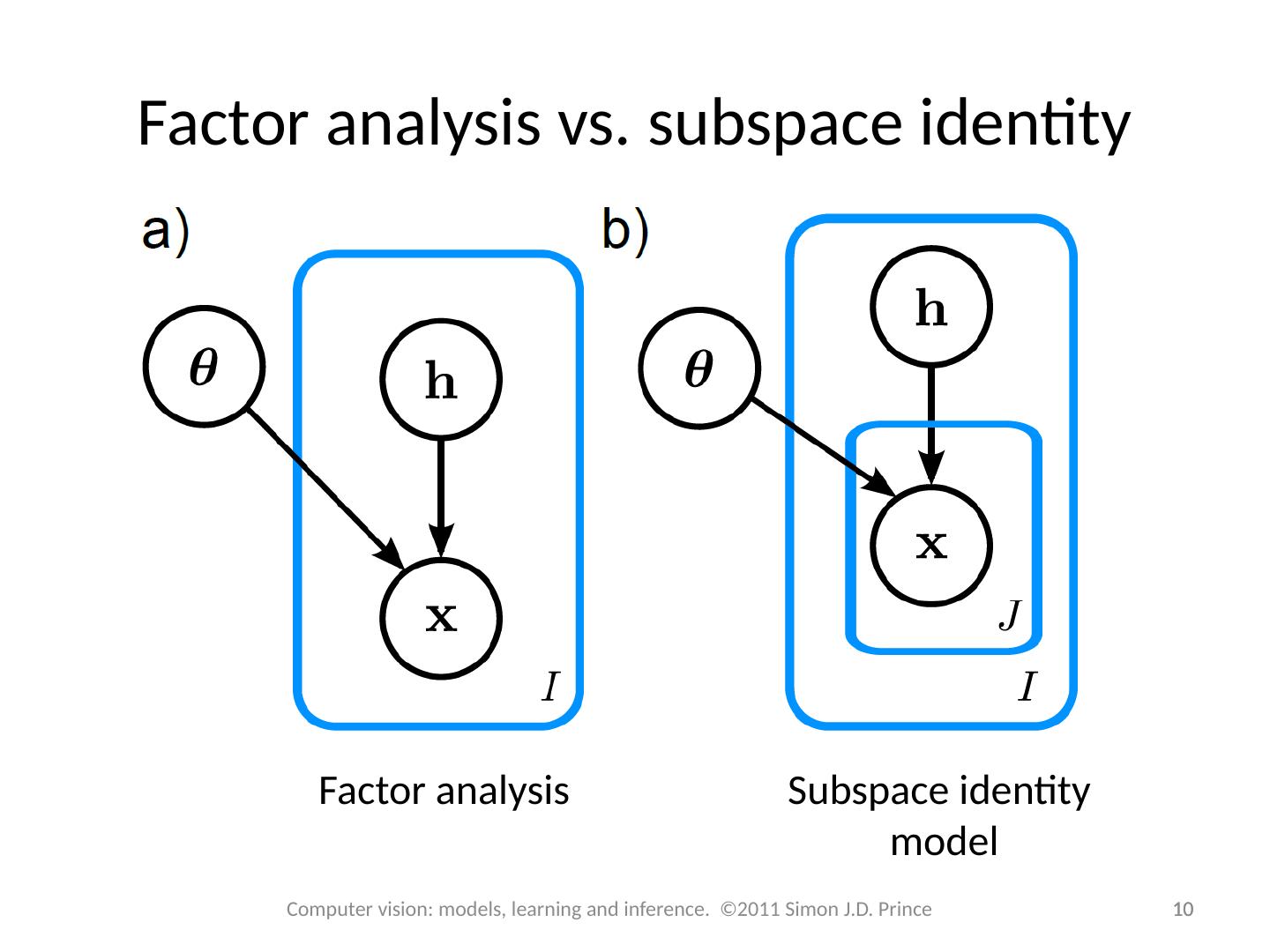
10 .Factor analysis vs. subspace identity 10 10 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince Factor analysis Subspace identity model

11 .Learning subspace identity model 11 11 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince E-Step: Extract moments :

12 .Learning subspace identity model 12 12 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince M-Step: E -Step:

13 .Subspace identity model 13 13 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince

14 .Subspace identity model 14 14 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince

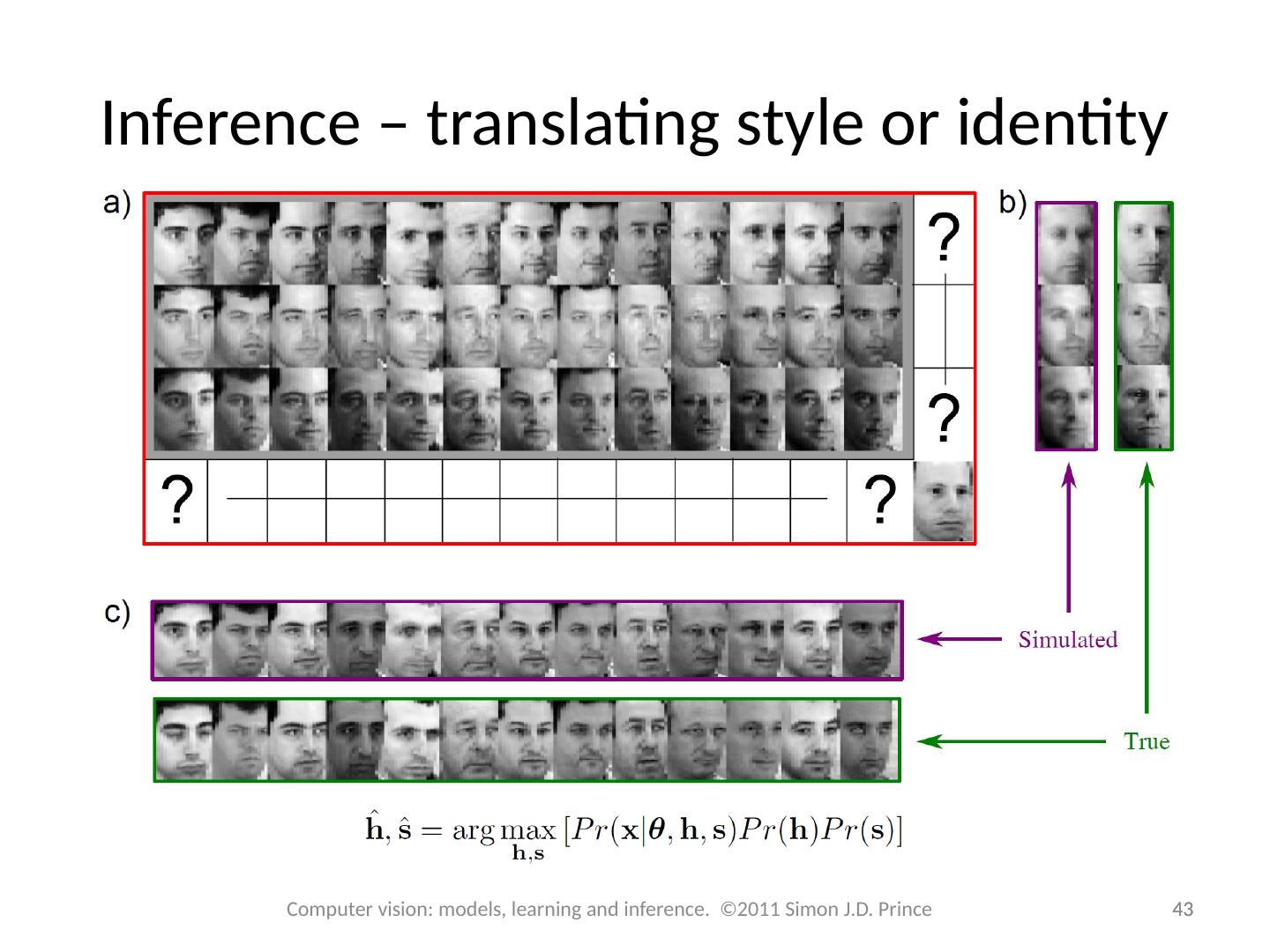
15 .Inference by comparing models 15 15 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince Model 1 – Faces match (identity shared) : Model 2 – Faces dont match (identities differ) : Both models have standard form of factor analyzer

16 .Inference by comparing models 16 16 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince Compute likelihood (e.g. for model zero) where Compute posterior probability using Bayes rule

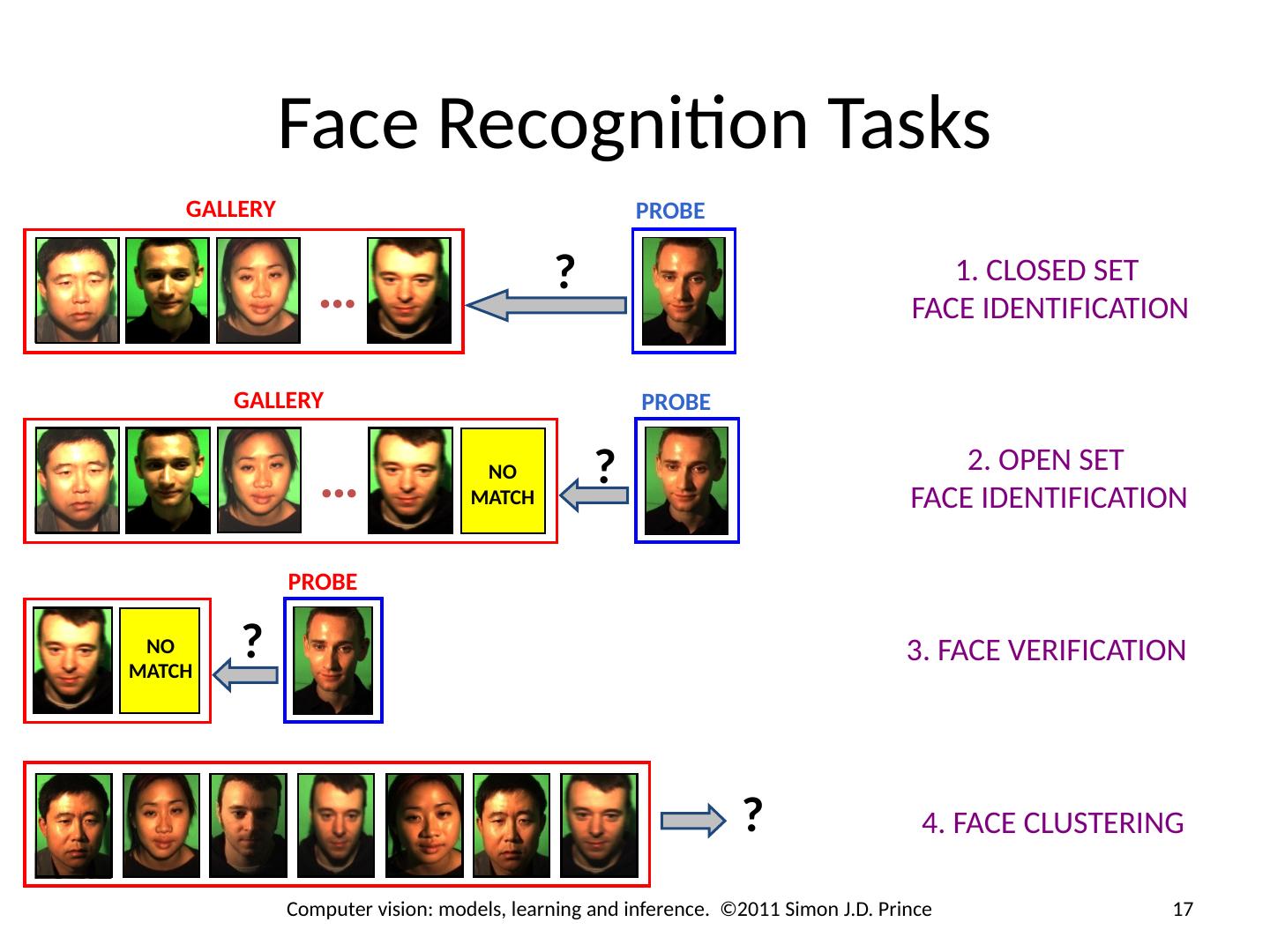
17 .Face Recognition Tasks PROBE … GALLERY ? 1. CLOSED SET FACE IDENTIFICATION … GALLERY PROBE ? NO MATCH 2. OPEN SET FACE IDENTIFICATION PROBE ? NO MATCH 3. FACE VERIFICATION 4. FACE CLUSTERING ? 17 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince

18 .Inference by comparing models 18 18 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince

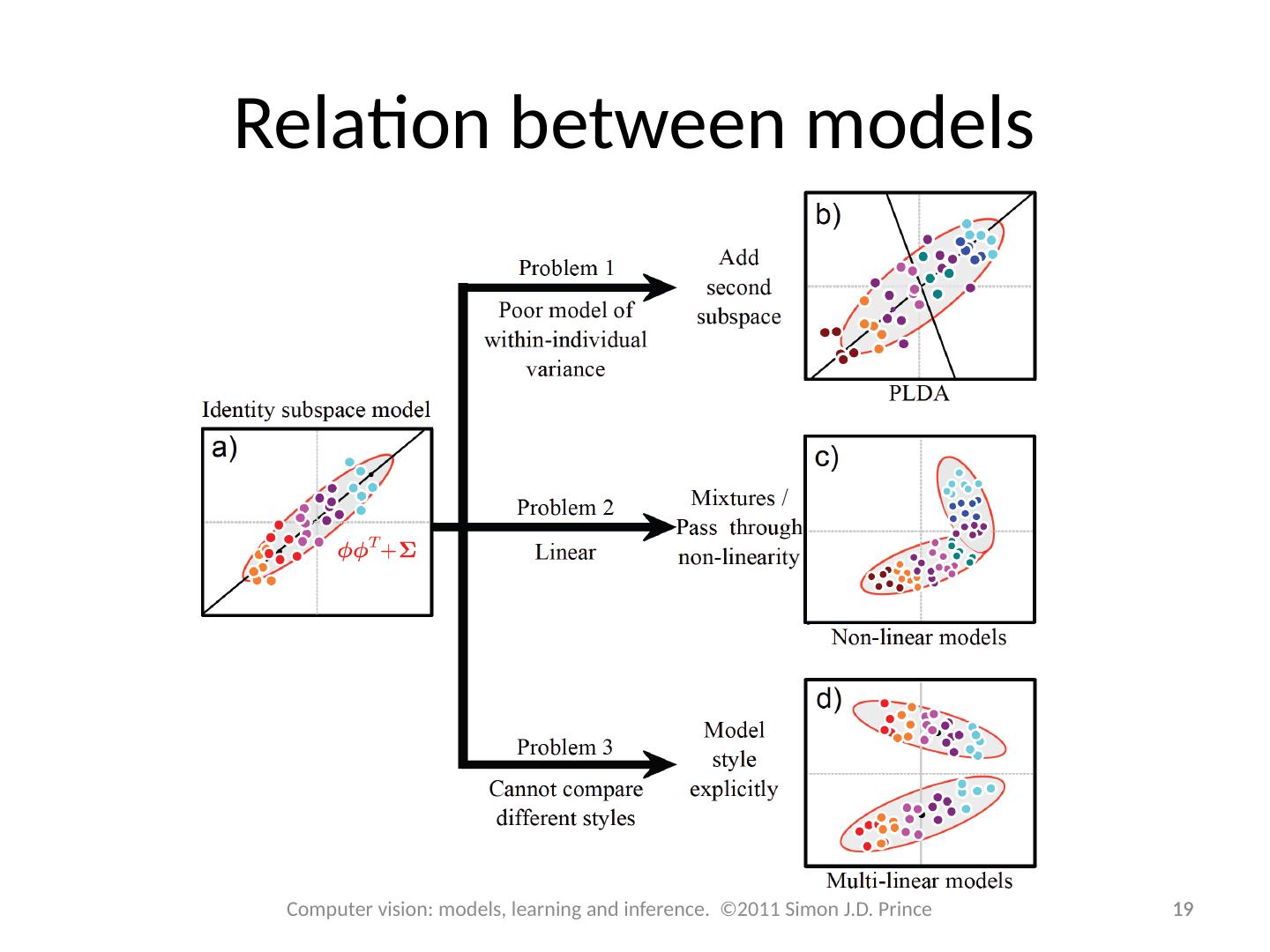
19 .Relation between models 19 19 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince

20 .Structure 20 20 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince Factor analysis review Subspace identity model Linear discriminant analysis Non-linear models Asymmetric bilinear model Symmetric bilinear model Applications

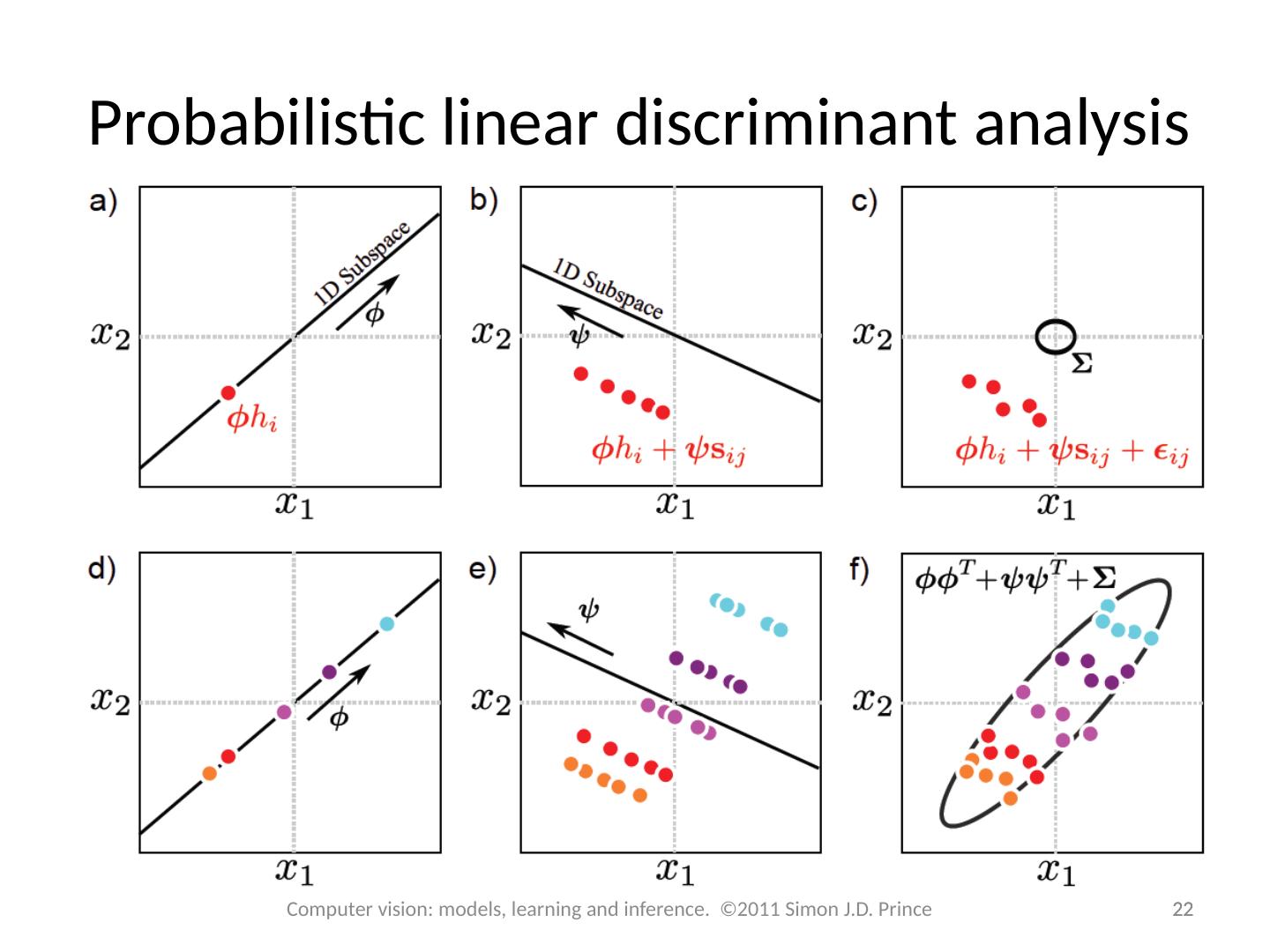
21 .Probabilistic linear discriminant analysis 21 21 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince Generative equation: Probabilistic form:

22 .Probabilistic linear discriminant analysis 22 22 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince

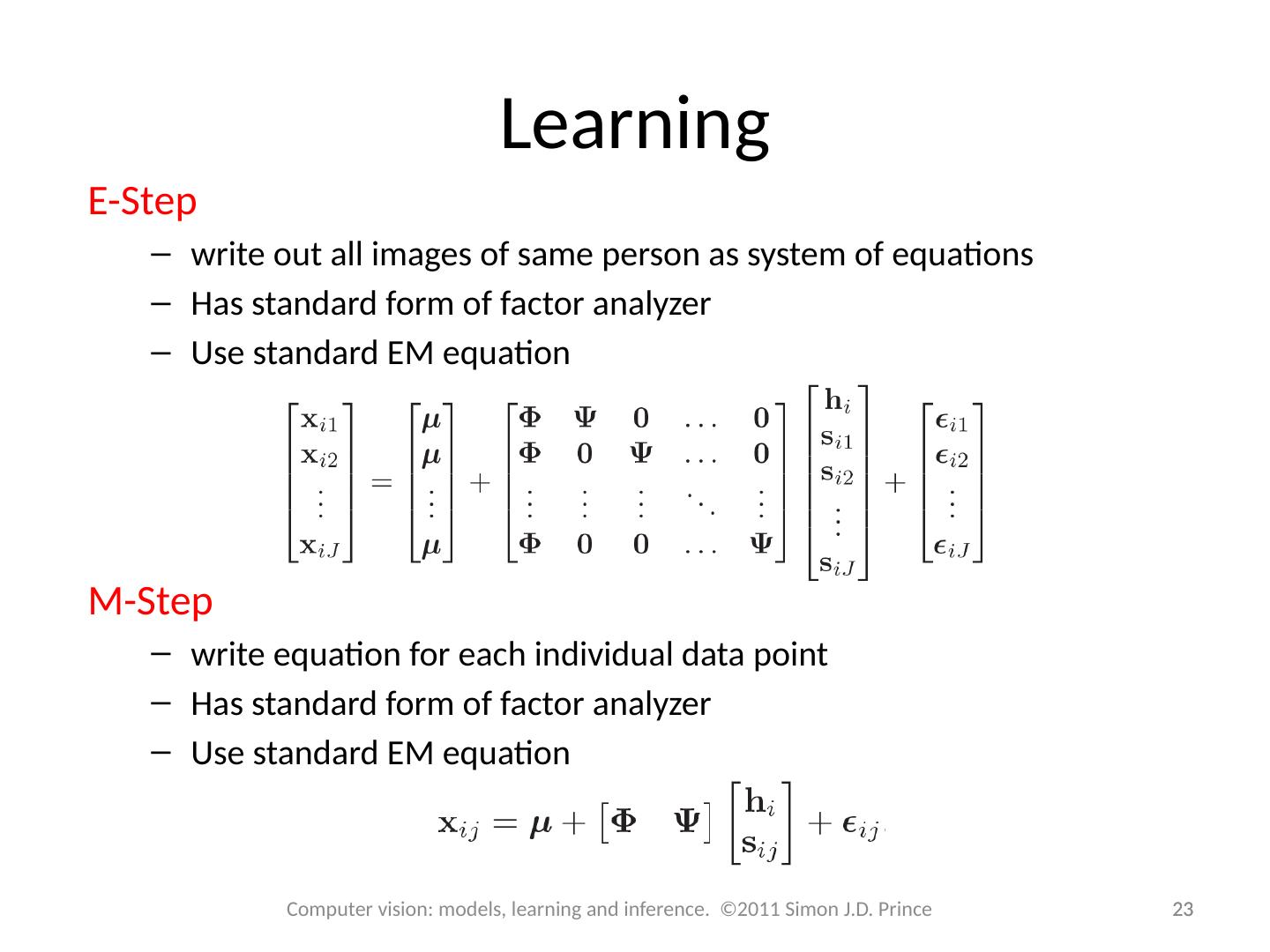
23 .Learning 23 23 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince E-Step write out all images of same person as system of equations Has standard form of factor analyzer Use standard EM equation M -Step write equation for each individual data point Has standard form of factor analyzer Use standard EM equation

24 .Probabilistic linear discriminant analyis 24 24 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince

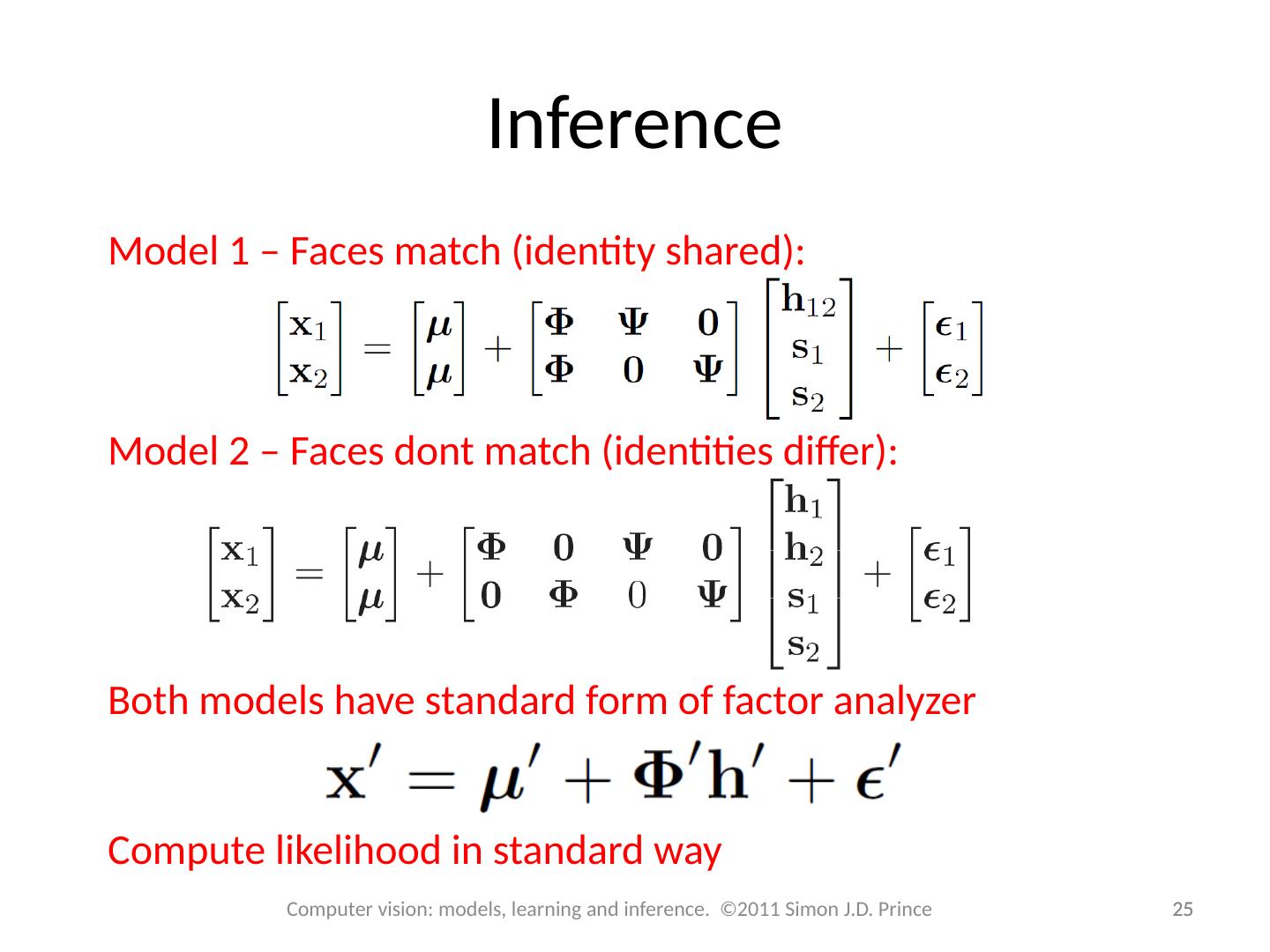
25 .Inference 25 25 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince Model 1 – Faces match (identity shared) : Model 2 – Faces dont match (identities differ) : Both models have standard form of factor analyzer Compute likelihood in standard way

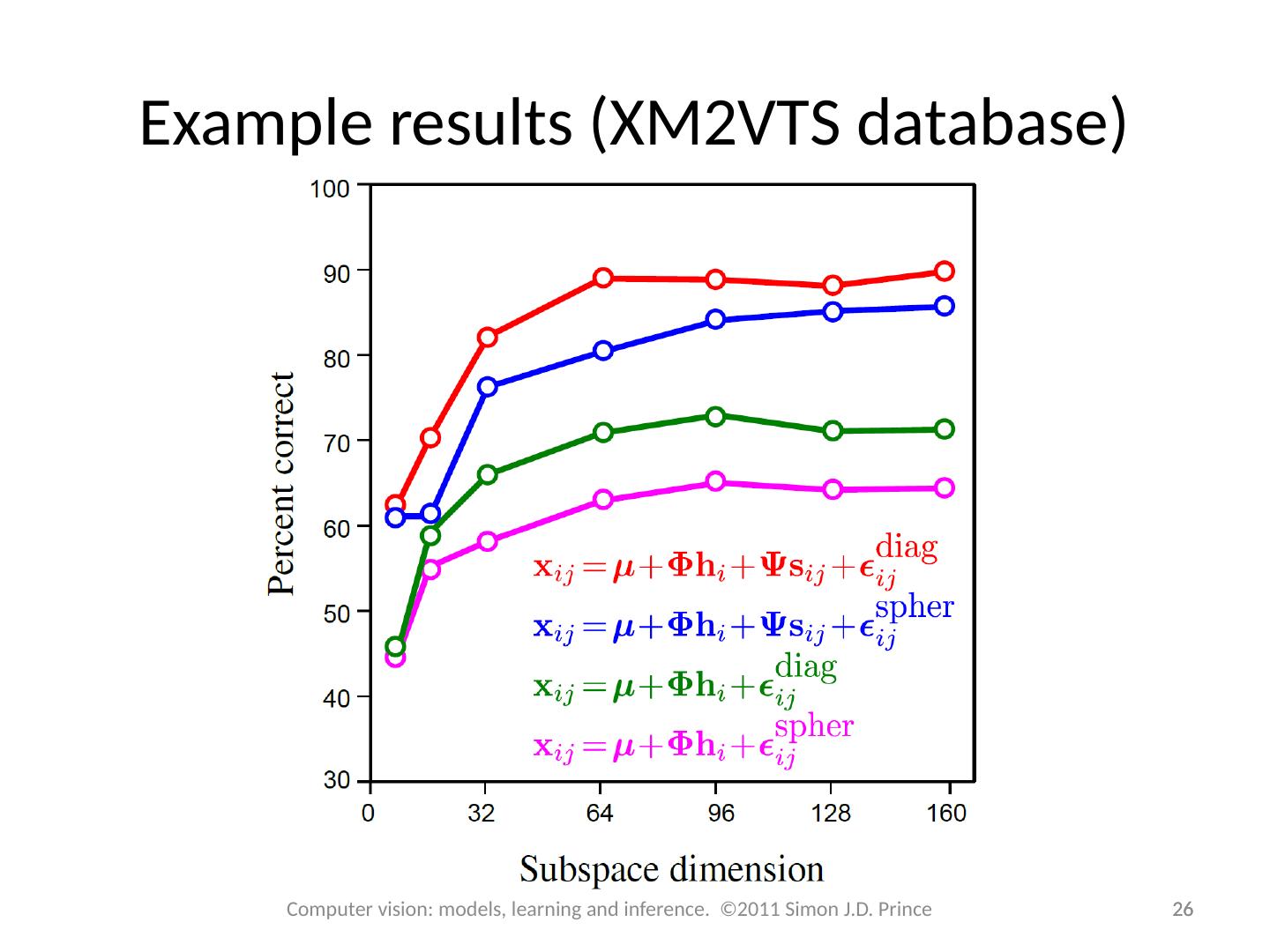
26 .Example results (XM2VTS database) 26 26 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince

27 .Structure 27 27 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince Factor analysis review Subspace identity model Linear discriminant analysis Non-linear models Asymmetric bilinear model Symmetric bilinear model Applications

28 .Non-linear models (mixture) 28 28 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince Mixture model can describe non-linear manifold. Introduce variable c i which represents which cluster To be the same identity, must also belong to the same cluster

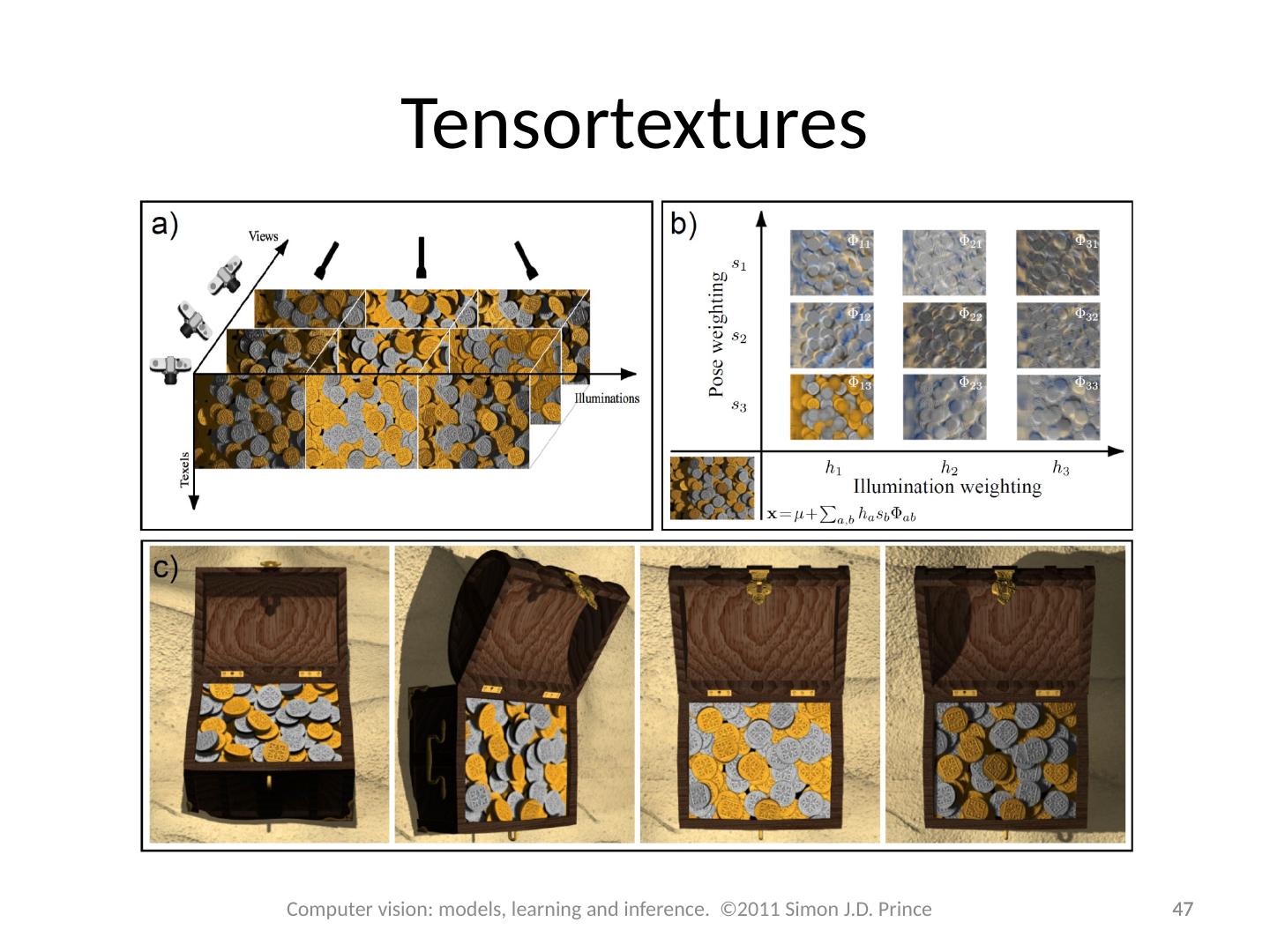
29 .Non-linear models (kernel) 29 29 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince Pass hidden variable through non-linear function f[ ]. Leads to kernelized algorithm Identity equivalent of GPLVM