02_线性方程组直接解法

1 .第二讲 线性方程组直接解法 1 Gauss 消去法和 LU 分解 2 特殊方程组的求解 3 扰动分析 4 误差分析 5 解的改进和条件数估计 

2 . 线性方程组的求解方法 • 直接法: LU 分解, Cholesky 分解, ... • 迭代法: 古典迭代法, Krylov 子空间迭代法 本章介绍直接法, 即 Gauss 消去法 或 PLU 分解 直接法优点: 稳定可靠 → 在工程计算中很受欢迎 直接法缺点: 运算量大 O(n3 ) → 不适合大规模稀疏线性方程组 (针对特殊结构矩阵的快速方法除外) 2/95 

3 .1 Gauss 消去法和 LU 分解 1.1 LU 分解 1.2 LU 分解的实现 1.3 IKJ 型 LU 分解 1.4 待定系数法计算 LU 分解 1.5 三角方程求解 1.6 选主元 LU 分解 1.7 矩阵求逆 3/95 

4 .1.1 LU 分解 考虑线性方程组 Ax = b (2.1) 其中 A ∈ Rn×n 非奇异, b ∈ Rn 为给定的右端项. Gauss 消去法本质上就是对系数矩阵 A 进行 LU 分解: A = LU (2.2) 其中 L 是单位下三角矩阵, U 为非奇异上三角矩阵. 分解 (2.2) 就称为 LU 分解 4/95 

5 . { Ly = b, Ax = b ⇐⇒ =⇒ 只需求解两个三角方程组 U x = y. 算法 1.1 Gauss 消去法 1: 将 A 进行 LU 分解: 2: A = LU , 其中 L 为单位下三角矩阵, U 为非奇异上三角矩阵; 3: 向前回代: 求解 Ly = b, 即得 y = L−1 b; 4: 向后回代: 求解 U x = y, 即得 x = U −1 y = (LU )−1 b = A−1 b. 5/95 

6 .† 需要指出的是: A 非奇异, 则解存在唯一, 但并不一定存在 LU 分解! 定理 (LU 分解的存在性和唯一性) 设 A ∈ Rn×n . 则存在唯一的单位下 三角矩阵 L 和非奇异上三角矩阵 U , 使得 A = LU 的充要条件是 A 的 所有顺序主子矩阵 Ak = A(1 : k, 1 : k) 都非奇异, k = 1, 2, . . . , n. (板书) 6/95 

7 .1.2 LU 分解的实现 — 矩阵初等变换 给定一个矩阵   a11 a12 · · · a1n    a21 a22 · · · a2n  A=  .. ..  ∈ Rn×n .   . .  an1 an2 · · · ann • 第一步: 假定 a11 ̸= 0, 构造矩阵   1 0 0 ··· 0 l 1 0 ··· 0  21    ai1 L1 =  l 0  31 1 ··· 0 ,  其中 li1 = , i = 2, 3, . . . , n.  .. ..  a11  . .  ln1 0 0 ··· 1 7/95 

8 .易知 L1 的逆为   1 0 0 ··· 0  −l 1 0 ··· 0  21    L−1 1 = −l  31 0 1 ··· 0 .   .. ..   . .  −ln1 0 0 ··· 1 用 L−1 1 左乘 A, 并将所得到的矩阵记为 A (1) ,则   a11 a12 · · · a1n  (1) (1)   0 a22 · · · a2n  A(1) = L−1 A  . . 1  . .. ..   . . .  (1) (1) 0 an2 · · · ann 即左乘 L−1 1 后, A 的第一列中除第一个元素外其它都变为 0. 8/95 

9 .• 第二步: 将上面的操作作用在 A(1) 的子矩阵 A(1) (2 : n, 2 : n) 上, 将 (1) 其第一列除第一个元素外都变为 0: 假定 a22 ̸= 0, 构造矩阵   1 0 0 ··· 0 0 1 0 ··· 0     (1) ai2 L2 =   0 l32 1 · · · 0 ,  其中 li2 = (1) , i = 3, 4, . . . , n.  .. .. ..  a22 . . .  0 ln2 0 · · · 1 用 L−1 2 左乘 A (1) , 并将所得到的矩阵记为 A(2) , 则   a11 a12 a13 · · · a1n  (1)   0 a(1) (1) 22 a23 · · · a2n     0 0 a(2) · · · a3n  (2) A(2) = L−1 −1 −1 2 A = L2 L1 A =  33 .  . .. ..   .. .. .   . .  (2) (2) 0 0 an3 · · · ann 9/95 

10 .• 依此类推, 假定 akk (k−1) ̸= 0 (k = 3, 4, . . . , n − 1), 则我们可以构造一系 列的矩阵 L3 , L4 , . . . , Ln−1 , 使得   a11 a12 a13 · · · a1n  (1)   0 a(1) 22 a23 · · · a2n  (1)    0 0 a(2) · · · a(2)  L−1 · · · L−1 −1 L A =  33 3n  ≜ U → 上三角 n−1 2 1  . .. .. . .   .. .   . .  (n−1) 0 0 0 · · · ann 于是可得 A = LU 其中   1 0 0 ··· 0 l 0 ··· 0  21 1    L = L1 L2 · · · Ln−1 = l  31 l32 1 ··· 0   .. .. ..   . . .  ln1 ln2 ln3 · · · 1 10/95 

11 .算法 1.2 LU 分解 1: for k = 1 to n − 1 do 2: for i = k + 1 to n do 3: lik = aik /akk % 计算 L 的第 k 列 4: end for 5: for j = k to n do 6: ukj = akj % 计算 U 的第 k 行 7: end for 8: for i = k + 1 to n do 9: for j = k + 1 to n do 10: aij = aij − lik ukj % 更新 A(k + 1 : n, k + 1 : n) 11: end for 12: end for 13: end for 11/95 

12 . Gauss 消去法的运算量 由算法 1.2 可知, LU 分解的运算量 (加减乘除) 为   ∑ ∑ n−1 n ∑n ∑ n ∑( n−1 ) 2  1+ 2 = n − i + 2(n − i)2 = n3 + O(n2 ). i=1 j=i+1 j=i+1 i=1 3 k=i+1 2 3 加上回代过程的运算量 O(n2 ), 总运算量为 n + O(n2 ) 3 12/95 

13 .† 评价算法的一个主要指标是执行时间, 但这依赖于计算机硬件和编 程技巧等, 因此直接给出算法执行时间是不太现实的. 所以我们通常 是统计算法中算术运算 (加减乘除) 的次数. † 在数值算法中, 大多仅仅涉及加减乘除和开方运算. 一般地, 加减运 算次数与乘法运算次数具有相同的量级, 而除法运算和开方运算次 数具有更低的量级. † 为了尽可能地减少运算量, 在实际计算中, 数, 向量和矩阵做乘法运 算时的先后执行次序为: 先计算数与向量的乘法, 然后计算矩阵与向 量的乘法, 最后才计算矩阵与矩阵的乘法. 13/95 

14 . 矩阵 L 和 U 的存储 当 A 的第 i 列被用于计算 L 的第 i 列后, 在后面的计算中不再被使用. 同样地, A 的第 i 行被用于计算 U 的第 i 行后, 在后面计算中也不再使用. 为了节省存储空间, 在计算过程中将 L 的第 i 列存放在 A 的第 i 列, 将 U 的第 i 行存放在 A 的第 i 行, 这样就不需要另外分配空间存储 L 和 U . 计算结束后, A 的上三角部分为 U , 其绝对下三角部分为 L 的绝对下三角 部分 (L 的对角线全部为 1, 不需要存储). 14/95 

15 .算法 1.3 LU 分解 1: for k = 1 to n − 1 do 2: for i = k + 1 to n do 3: aik = aik /akk 4: for j = k + 1 to n do 5: aij = aij − aik akj 6: end for 7: end for 8: end for † 根据指标的循环次序, 算法 1.3 也称为 KIJ 型 LU 分解. 实际计算中一 般不建议使用: 对指标 k 的每次循环, 都需要更新 A 的第 k + 1 至第 n 行, 这种反复读取数据的做法会使得计算效率大大降低. 对于按行存储的数据结构, 一般采用后面介绍的 IKJ 型 LU 分解. 15/95 

16 . MATLAB 源代码 1 LU 分解的 Matlab 代码 (KIJ 型) 1 % Matlab code : LU 分解 2 function A = mylu(A) 3 n=size(A,1); 4 for k=1:n-1 5 if A(k,k) == 0 6 fprintf('Error: A(%d,%d)=0!\n', k, k); 7 return; 8 end 9 for i=k+1:n 10 A(i,k)=A(i,k)/A(k,k); 11 for j=k+1:n 12 A(i,j)=A(i,j)-A(i,k)*A(k,j); 13 end 14 end 15 end 16/95 

17 .为了充分利用 Matlab 的向量运算优势, 提高运算效率, 程序可改写为 MATLAB 源代码 2 LU 分解 (KIJ 型) 1 function A = mylu(A) 2 n=size(A,1); 3 for k=1:n-1 4 if A(k,k) == 0 5 fprintf('Error: A(%d,%d)=0!\n', k, k); 6 return; 7 end 8 A(k+1:n,k)=A(k+1:n,k)/A(k,k); 9 A(k+1:n,k+1:n)=A(k+1:n,k+1:n)-A(k+1:n,k)*A(k,k+1:n); 10 end 17/95 

18 .1.3 IKJ 型 LU 分解 如果数据是按行存储的, 如 C/C++, 我们一般采用下面的 IKJ 型 LU 分解. 算法 1.4 LU 分解 (IKJ 型) 1: for i = 2 to n do 2: for k = 1 to i − 1 do 3: aik = aik /akk 4: for j = k + 1 to n do 5: aij = aij − aik akj 6: end for 7: end for 8: end for 18/95 

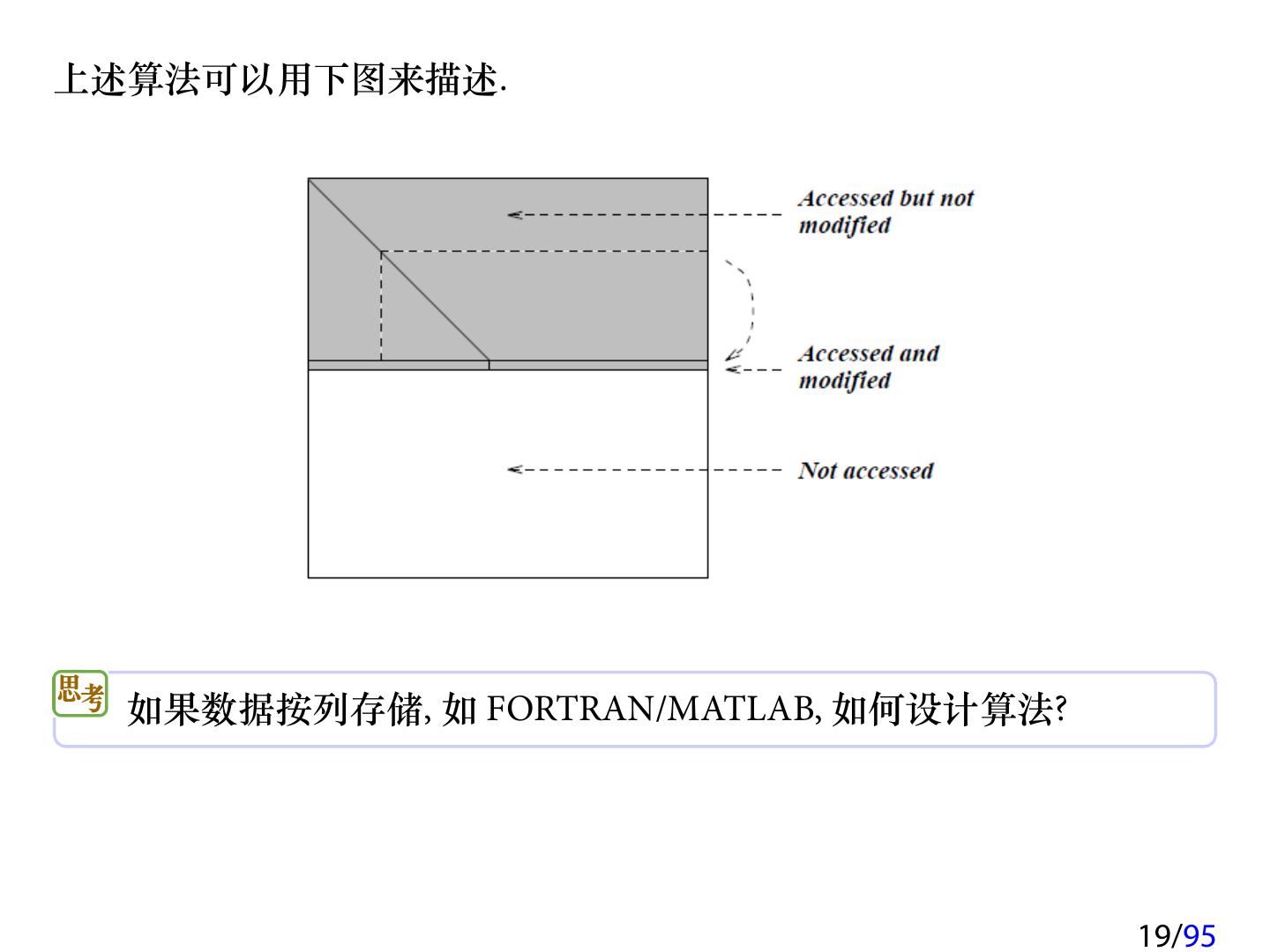
19 .上述算法可以用下图来描述. 如果数据按列存储, 如 FORTRAN/MATLAB, 如何设计算法? 19/95 

20 .1.4 待定系数法计算 LU 分解 设 A = LU , 即      a11 a12 a13 · · · a1n 1 u11 u12 u13 · · · u1n a a a · · · a  l  · · · u2n   21 22 23 2n   21 1  u22 u23        a31 a32 a33 · · · a3n  =  l31 l32 1  u33 · · · u2n        .. .. .   . ..  .. .   . . ..   .. .  . ..  an1 an2 an3 · · · ann ln1 ln2 · · · ln,n−1 1 unn (1) 比较等式两边的第一行, 可得 u1j = a1j , j = 1, 2, . . . , n. 再比较等式两边的第一列, 可得 ai1 = li1 u11 ⇒ li1 = ai1 /u11 , i = 2, 3, . . . , n. (2) 比较等式两边的第二行, 可得 a2j = l21 u1j ⇒ u2j = a2j − l21 uij , j = 2, 3, . . . , n. 20/95 

21 . 再比较等式两边的第二列, 可得 ai2 = li1 u12 + li2 u22 ⇒ li1 = (ai2 − li1 u12 )/u22 , i = 3, 4, . . . , n. (3) 以此类推, 第 k 步时, 比较等式两边的第 k 行, 可得 ukj = akj − (lk1 u1j + · · · + lk,k−1 uk−1,j ), j = k, k + 1, . . . , n. 比较等式两边的第 k 列, 可得 lik = (aik −li1 u1k −· · ·−li,k−1 uk−1,k )/ukk , i = k+1, k+2, . . . , n. 直到第 n 步, 即可计算出 L 和 U 的所有元素. 21/95 

22 .同样, 我们可以利用 A 来存储 L 和 U . 算法描述如下: 算法 1.5 LU 分解 (待定系数法或 Doolittle 方法) 1: for k = 1 to n do ∑ k−1 2: akj = akj − aki aij , j = k, k + 1, . . . , n i=1   1  ∑ k−1 3: aik = aik − aij ajk , i = k + 1, k + 2, . . . , n akk j=1 4: end for 22/95 

23 . MATLAB 源代码 3 待定系数法 LU 分解 1 function A = mylu2(A) 2 [n,n]=size(A); 3 for k=1:n 4 A(k,k)=A(k,k)-A(k,1:k-1)*A(1:k-1,k); 5 if (A(k,k)==0) 6 fprintf('Error: A(%d,%d)=0!\n', i,i); 7 return; 8 end 9 A(k,k+1:n)=A(k,k+1:n)-A(k,1:k-1)*A(1:k-1,k+1:n); 10 A(k+1:n,k)=A(k+1:n,k)-A(k+1:n,1:k-1)*A(1:k-1,k); 11 A(k+1:n,k)=A(k+1:n,k)/A(k,k); 12 end 23/95 

24 .1.5 三角方程求解 得到 A 的 LU 分解后, 我们最后需要用回代法求解两个三角方程组 Ly = b, U x = y. 算法 1.6 向前回代求解 Ly = b 1: y1 = b1 2: for i = 2 : n do 3: s = bi 4: for j = 1 : i − 1 do 5: s = s − uij xj 6: end for 7: xi = s 8: end for 24/95 

25 .如果数据是按列存储的, 则采用列存储方式效率会高一些. 下面是按列存 储方式求解上三角方程组. 算法 1.7 向后回代求解 U x = y 1: xn = yn /unn 2: for i = n − 1 : −1 : 1 do 3: s = yi 4: for j = i + 1 : n do 5: s = s − uij xj 6: end for 7: xi = s/uii 8: end for 这两个算法的运算量均为 n2 + O(n). 25/95 

26 .1.6 选主元 LU 分解 • 在 LU 分解算法 1.2 中, 我们称 a(k−1) kk (k−1) 为主元. 如果 akk = 0, 则算 法就无法进行下去. • 即使 a(k−1) kk (k−1) 不为零, 但如果 |akk | 的值很小, 由于舍入误差的原因, 也可能会给计算结果带来很大的误差. • 此时我们就需要通过 选主元 来解决这个问题. 26/95 

27 .例 用 LU 分解求解线性方程组 Ax = b, 其中 [ ] [ ] 0.02 61.3 61.5 A= , b= , 3.43 −8.5 25.8 要求在运算过程中保留 3 位有效数字. (x1 ≈ −20.7, x2 ≈ 1.01) (板书) 易知, 方程的精确解为 x1 = 10.0 和 x2 = 1.00. 我们发现 x1 的误差非常 大. 导致这个问题的原因就是 |a11 | 太小, 用它做主元时会放大舍入误差. 所以我们需要选主元. 27/95 

28 .选主元 LU 分解 定理 设 A ∈ Rn×n 非奇异, 则存在置换矩阵 P1 , P2 , 以及单位下三角矩 阵 L 和非奇异上三角矩阵 U , 使得 P1 AP2 = LU . 其中 P1 和 P2 中只有 一个是必需的. (板书) 第 k 步时, 如何选取置换矩阵 P1 和 P2 ？ 1. 选取 P1 和 P2 使得主元为剩下的矩阵中绝对值最大, 这种选取方法 称为 “全主元 Gauss 消去法”, 简称 GECP 2. 选取 P1 和 P2 使得主元为第 k 列中第 k 到第 n 个元素中, 绝对值最 大, 这种选取方法称为 “部分选主元 Gauss 消去法”, 简称 GEPP 此时 P2 = I, 因此也称为列主元 Gauss 消去法. • GECP 比 GEPP 更稳定, 但工作量大, 实际很少使用. • GEPP 算法能保证 L 所有的元素的绝对值都不超过 1. 28/95 

29 .算法 1.8 部分选主元 LU 分解 1: p = 1 : n % 用于记录置换矩阵 2: for i = 1 to n − 1 do 3: aki = maxi≤j≤n |aji | % 选列主元 4: if k ∼= i then 5: for j = 1 to n do 6: tmp = aij , aij = akj , akj = tmp % 交换第 i 行与第 k 行 7: end for 8: tmp = p(k), p(k) = p(i), p(i) = tmp % 更新置换矩阵 9: end if 10: for j = i + 1 to n do 11: aji = aji /aii % 计算 L 的第 i 列 12: end for 13: for j = i + 1 to n do 14: for k = i + 1 to n do