Markov Decision Processes

1 .MARKOV DECISION PROCESSES 

2 . The material for this talk is drawn from the slides, notes and lectures from several offerings of the CS181 course at Harvard University:  CS181 Intelligent Machines: Perception, Learning and Uncertainty, Sarah Finney, Spring 2009  CS181 Intelligent Machines: Perception, Learning and Uncertainty, Prof. David C Brooks, Spring 2011 REFERENCES  CS181 – Machine Learning, Prof. Ryan P. Adams, Spring 2014. https://github.com/wihl/cs181- spring2014  CS181 – Machine Learning, Prof. David Parkes, Spring 2017. https://harvard-ml-courses.github.io/cs181- web-2017/ 

3 . 1. Introduction o Types of Machine Learning o Decision Theory 2. Markov Decision Processes o Definitions OVERVIEW o Examples 3. MDP Solutions o finite horizon techniques • expectimax • value iteration o Infinite horizon techniques • value iteration • policy iteration 

4 . TYPES OF MACHINE LEARNING There are (at least) 3 broad categories of machine learning problems: Supervised Learning 𝑫𝒂𝒕𝒂 = 𝒙𝟏 , 𝒚𝟏 , … , 𝒙𝒏 , 𝒚𝒏 e.g., linear regression, decision trees, SVMs Unsupervised Learning 𝑫𝒂𝒕𝒂 = 𝒙𝟏 , , … , 𝒙𝒏 e.g., K-means, HAC, Gaussian mixture models Reinforcement Learning 𝑫𝒂𝒕𝒂 = 𝒔𝟏 , 𝒂𝟏 , 𝒓𝟏 , 𝒔𝟐 , 𝒂𝟐 , 𝒓𝟐 … an agent learns to act in an uncertain environment by training on data that are sequences of state, action, reward. 

5 . DECISION THEORY The three components of the decision theoretic framework MDPs: Probability Use probability to model uncertainty about the domain. Utility Use utility to model an agent’s objectives. Decision Policy The goal is to design a decision policy, describing how the agent should act in all possible states in order to maximize its expected utility. 

6 . UNCERTAINTY MODELED WITH PROBABILITY • The agent may not know the current state of the world • The effects of the agent’s action might be unpredictable. • Things happen that are outside the agent’s control. • The agent may be uncertain about the correct model of the world. 

7 . “HAPPINESS” MODELED WITH UTILITY 1. Utility is a real number. 2. The higher the utility, the “happier” your robot is. 3. Utility is based on the assumptions of Utility Theory, which if obeyed, make you rational. 4. For example, if you prefer reward A to reward B, and you prefer reward B to reward C, then you should prefer reward A to reward C. 

8 . MARKOV DECISION PROCESSES • States: 𝒔𝟏 , … , 𝒔𝒏 • Actions: 𝒂𝟏 , … , 𝒂𝒎 • Reward Function: r 𝑠, 𝑎 ∈ 𝑅 • Transition model: p 𝑠′ 𝑠, 𝑎 

9 . MARKOV DECISION PROCESSES GOAL: find a policy π that tells you what action to take in each state. We want to find ‘rewarding’ policies. 

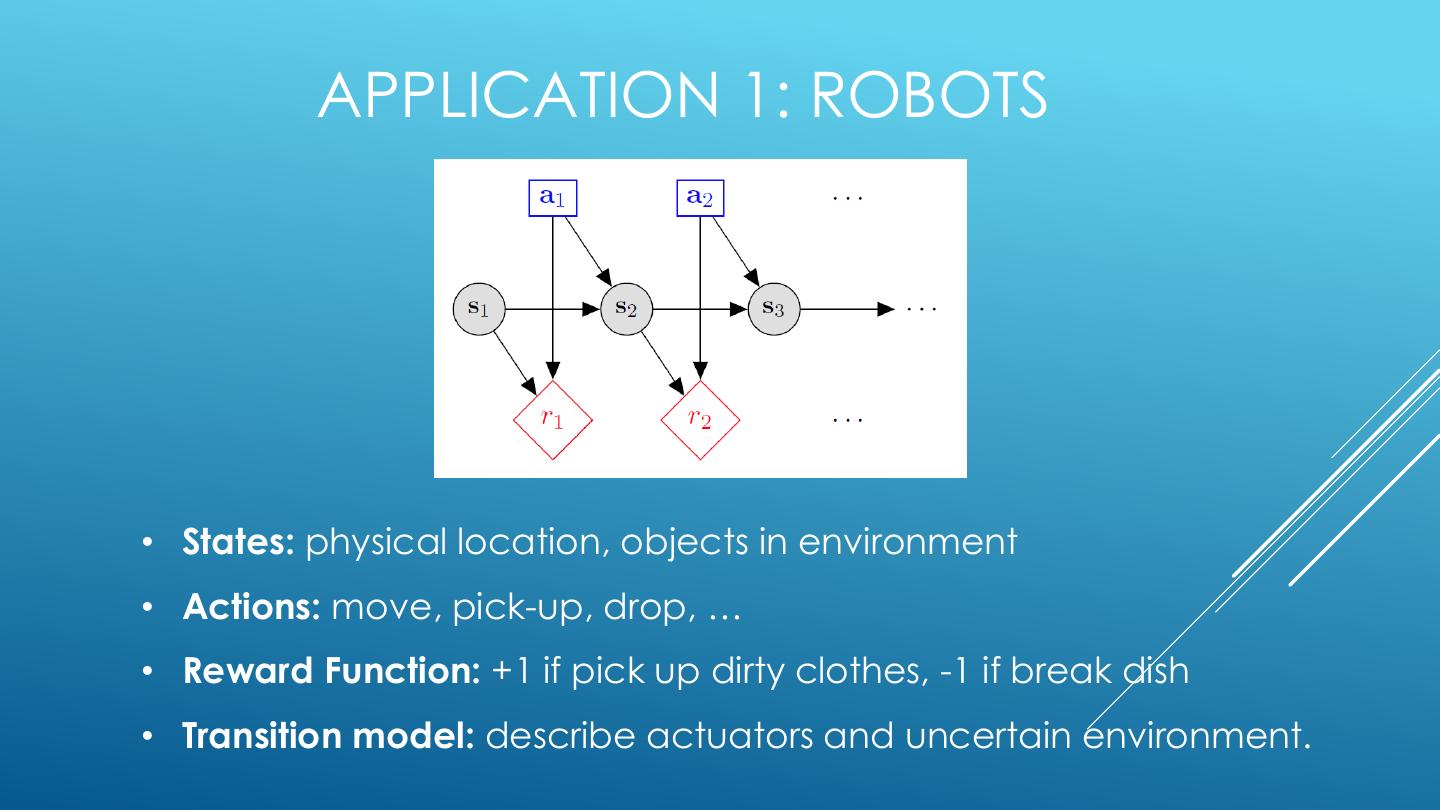
10 . APPLICATION 1: ROBOTS • States: physical location, objects in environment • Actions: move, pick-up, drop, … • Reward Function: +1 if pick up dirty clothes, -1 if break dish • Transition model: describe actuators and uncertain environment. 

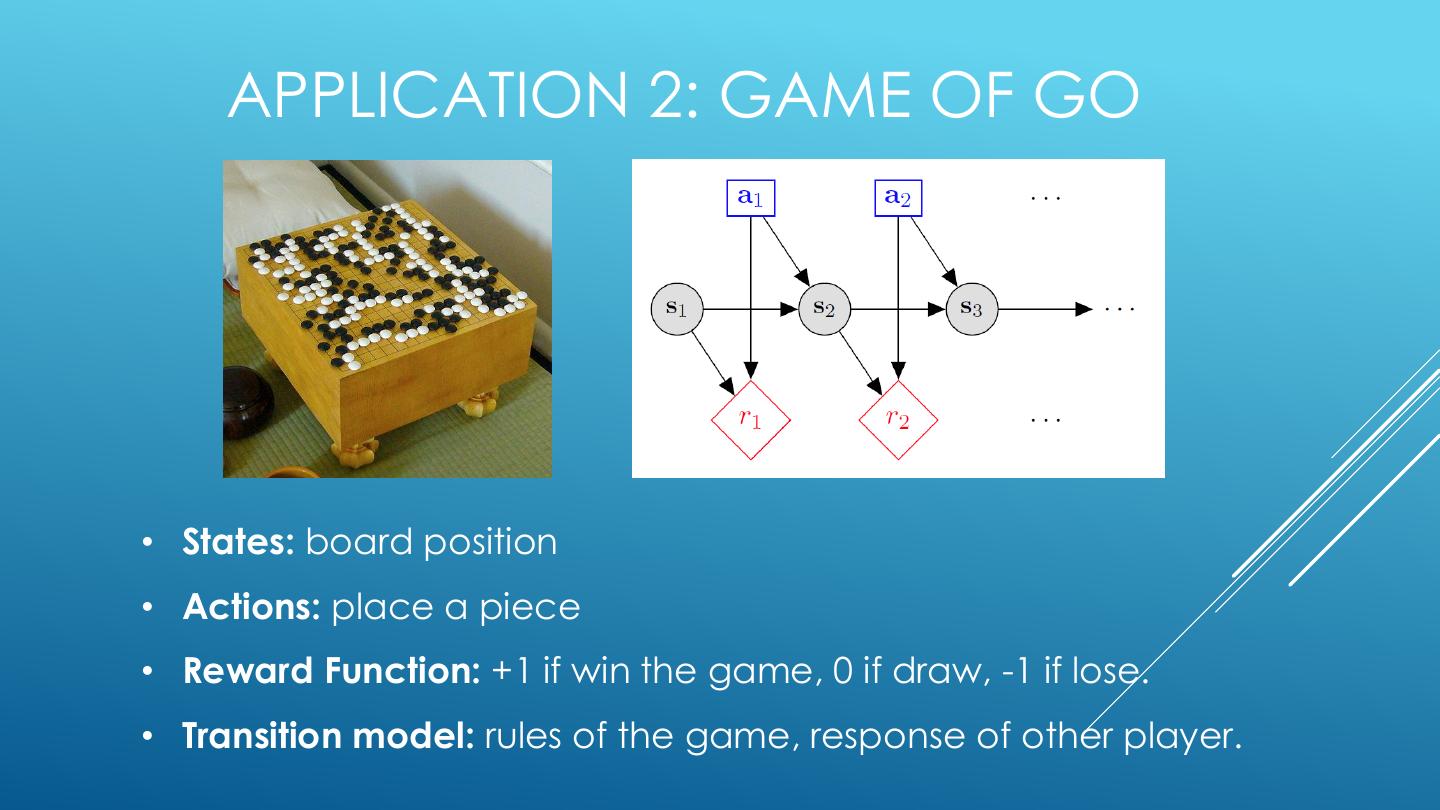
11 . APPLICATION 2: GAME OF GO • States: board position • Actions: place a piece • Reward Function: +1 if win the game, 0 if draw, -1 if lose. • Transition model: rules of the game, response of other player. 

12 .  AlphaGo (DeepMind) defeated Lee Sedol, 4-1 in March 2016, the top Go player in the world  AlphaGo combines Monte- Carlo tree search with deep neural nets (trained by supervised learning), with reinforcement learning.  Learns both a `policy network' (which action to play in which ALPHAGO VS. LEE SEDOL state) and a `value network' (estimate of value of an action under self-play). 

13 . APPLICATION 3: EMAIL ROUTING • States: - up/down for each server - current location and goal of each message. • Actions: choose path of servers for each message. • Reward Function: +1 for each message delivered to goal. • Transition model: describe network of servers. 

14 .APPLICATION 3: TRANSITION MODEL P(s’|s, a) depends on: - probability that each server fails given current load - probability that new messages enter the queue - probability that each message completes hop, given the state of the servers 

15 . SCOPE OF MDP APPLICABILITY The Markov Decision Process is a general probabilistic framework, and can be applied in many different scenarios. Planning  this talk • Full access to the MDP, compute an optimal policy. • “How do I act in a known world?" Policy Evaluation  this talk • Full access to the MDP, compute the `value' of a fixed policy. • “How will this plan perform under uncertainty?“ Reinforcement Learning (later) • Limited access to the MDP. • “Can I learn to act in an uncertain world?" 

16 . DIFFERENT OBJECTIVE CRITERIA • Sequence of 𝒔𝟏 , 𝒂𝟏 , 𝒓𝟏 , 𝒔𝟐 , 𝒂𝟐 , 𝒓𝟐 … ; discrete time t • Finite horizon, 𝑇 ≥ 1 steps 𝑇 𝑢𝑡𝑖𝑙𝑖𝑡𝑦 = ෍ r 𝑠𝑡 , 𝑎𝑡 𝑡=1 • Infinite horizon, discount factor 𝛾 𝜖 ሺ0, 1ሿ 𝑢𝑡𝑖𝑙𝑖𝑡𝑦 = r 𝑠1 , 𝑎1 + 𝛾 ∙ r 𝑠2𝑡 , 𝑎2 + 𝛾 2 ∙ r 𝑠3 , 𝑎3 + ⋯ 𝑇 𝑢𝑡𝑖𝑙𝑖𝑡𝑦 = ෍ 𝛾 𝑡−1 ∙ r 𝑠𝑡 , 𝑎𝑡 𝑡=1 

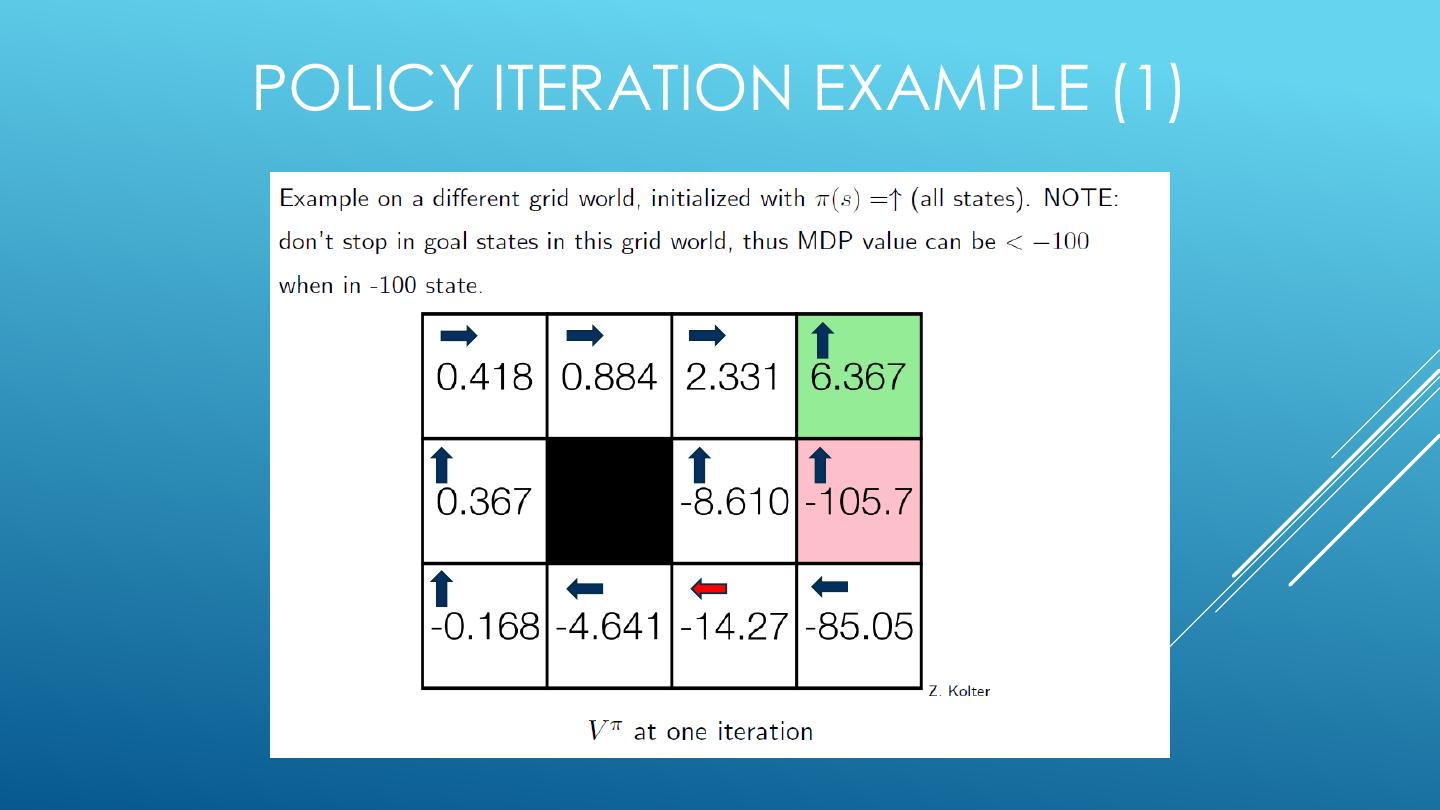
17 .OPTIMAL POLICY EXAMPLES: GRIDWORLD S Location on the grid 𝑥1 , 𝑦1 A Local movements ←, →, ↑, ↓ 𝐫 𝒔, 𝒂 Reward function, e.g., make it to a goal, don’t fall into a pit. 𝒑 𝒔′ |𝒔, 𝒂 Transition model e.g., d deterministic or slippages. 

18 .OPTIMAL POLICY: PERFECT ACTUATOR Goal • r 𝑔𝑜𝑎𝑙, 𝑎 = +1 and stop • r 𝑝𝑖𝑡, 𝑎 = −1 and stop Pit • r 𝑠, 𝑎 = −0.04 everywhere else. • Bounce off obstacles • Perfect actuator 

19 .OPTIMAL POLICY: IMPERFECT ACTUATOR • r 𝑔𝑜𝑎𝑙, 𝑎 = +1 and stop Goal • r 𝑝𝑖𝑡, 𝑎 = −1 and stop • r 𝑠, 𝑎 = −0.04 everywhere else. Pit • Bounce off obstacles • Imperfect actuator: - 0.8 probability of going straight - 0.1 probability of moving right - 0.1 probability of moving left 

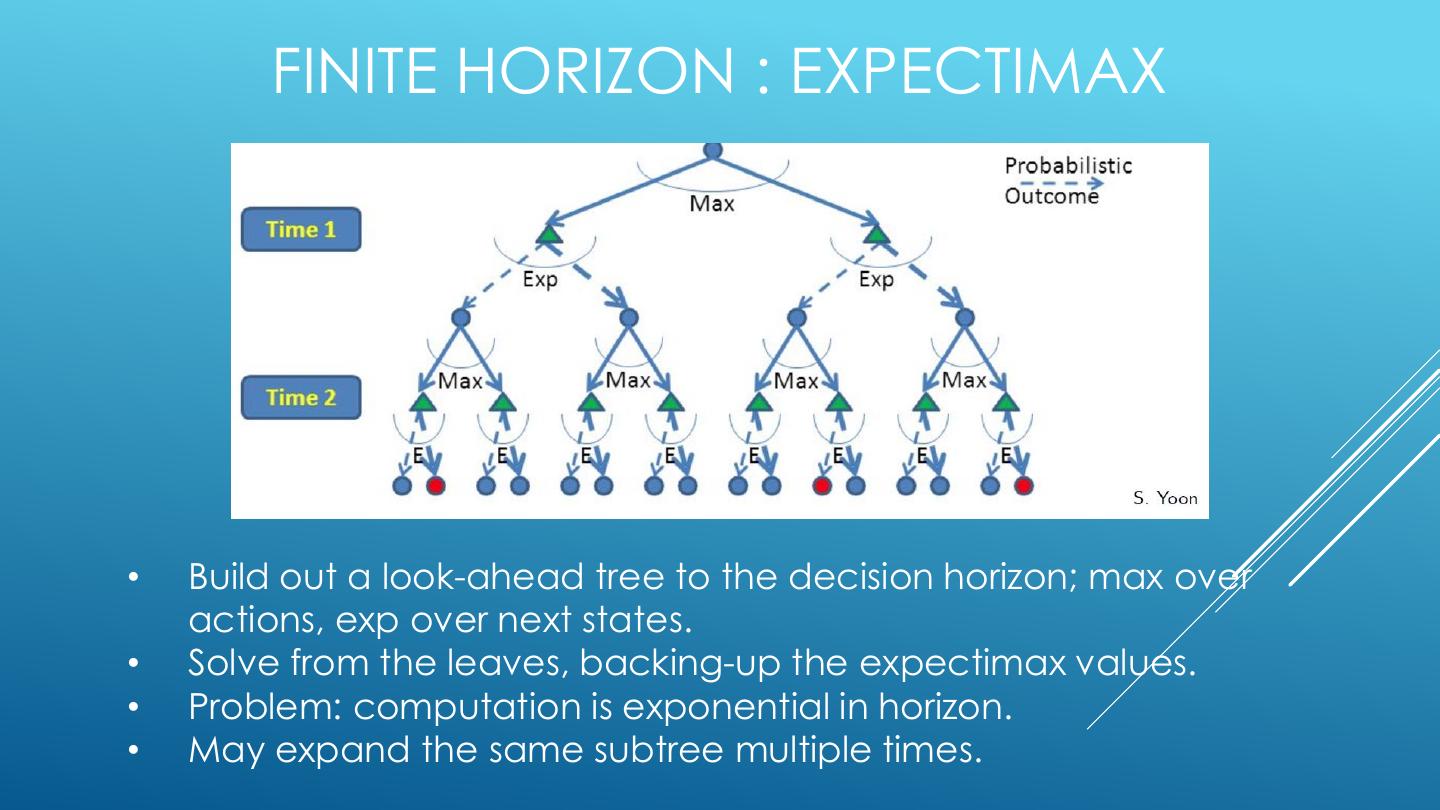
20 . FINITE HORIZON : EXPECTIMAX • Build out a look-ahead tree to the decision horizon; max over actions, exp over next states. • Solve from the leaves, backing-up the expectimax values. • Problem: computation is exponential in horizon. • May expand the same subtree multiple times. 

21 .EXPECTIMAX: A GAME AGAINST NATURE • Like a game except opponent is probabilistic • Strongly related minmax used in game theory • Nodes where you move: S ( ) • Nodes where nature moves: <S,A> ( ) 

22 . POLICY AND VALUES • Policy: action to take at each state • Value of state (node): expected total reward - Depends on policy 

23 .NOTATION 

24 .BASIC EQUATIONS 

25 .EXPECTIMAX ALGORITHM 

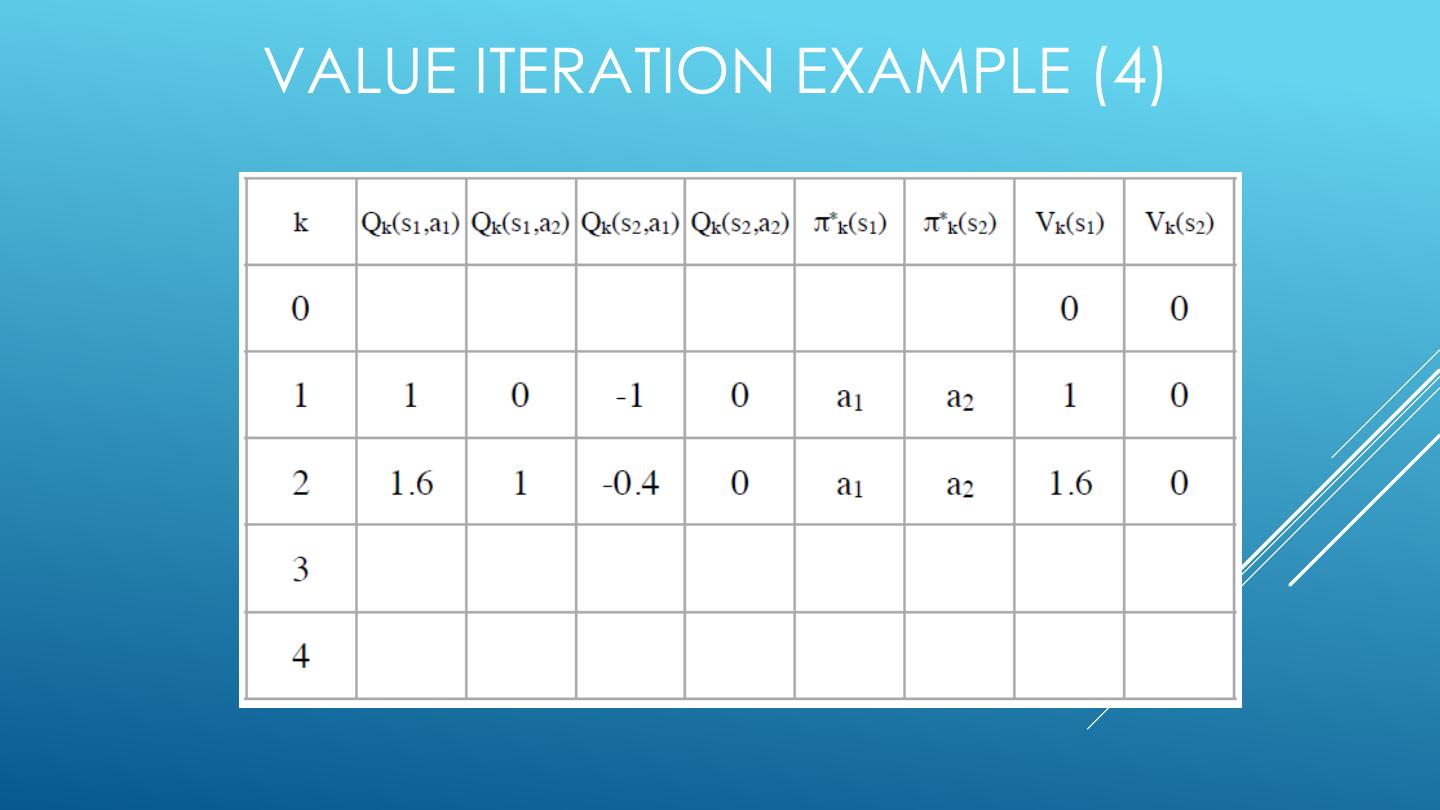
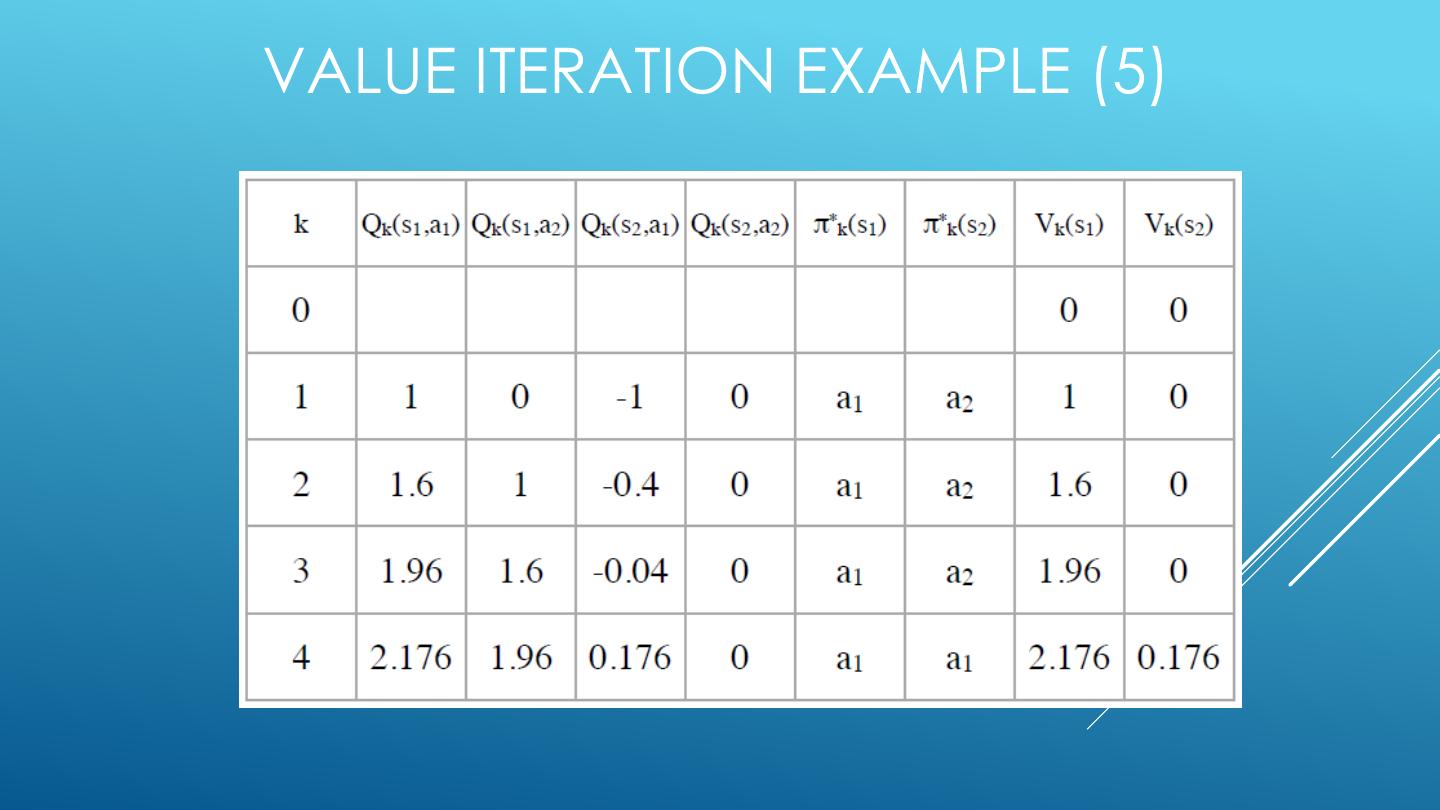
26 . 2-STATE FINITE HORIZON EXAMPLE <A1, 1.0, -1> <A1, 0.6, +1> <A2, 1.0, +0> S1 S2 <A1, 0.4, +1> <A2, 1.0, +0> States: S1, S2 Actions: A1,A2 Edges: <action, probability, value> 

27 .EXPECTIMAX: GAME TREE EXAMPLE (1) 

28 .EXPECTIMAX: GAME TREE EXAMPLE (2) 

29 .EXPECTIMAX: GAME TREE EXAMPLE (3)