Deep Laplacian Pyramid Networks for Fast and Accurate Super-Resolution

1 . Deep Laplacian Pyramid Networks for Fast and Accurate Super-Resolution Wei-Sheng Lai1 Jia-Bin Huang2 Narendra Ahuja3 Ming-Hsuan Yang1 1 University of California, Merced 2 Virginia Tech 3 University of Illinois, Urbana-Champaign http://vllab.ucmerced.edu/wlai24/LapSRN Abstract arXiv:1704.03915v2 [cs.CV] 9 Oct 2017 polation, to upscale input images to the desired spatial reso- lution before applying the network for prediction. This pre- Convolutional neural networks have recently demon- processing step increases unnecessary computational cost strated high-quality reconstruction for single-image super- and often results in visible reconstruction artifacts. Several resolution. In this paper, we propose the Laplacian Pyramid algorithms accelerate SRCNN by performing convolution Super-Resolution Network (LapSRN) to progressively re- on LR images and replacing the pre-defined upsampling op- construct the sub-band residuals of high-resolution images. erator with sub-pixel convolution [28] or transposed con- At each pyramid level, our model takes coarse-resolution volution [8] (also named as deconvolution in some of the feature maps as input, predicts the high-frequency residu- literature). These methods, however, use relatively small als, and uses transposed convolutions for upsampling to the networks and cannot learn complicated mappings well due finer level. Our method does not require the bicubic interpo- to the limited network capacity. Second, existing methods lation as the pre-processing step and thus dramatically re- optimize the networks with an 2 loss and thus inevitably duces the computational complexity. We train the proposed generate blurry predictions. Since the 2 loss fails to cap- LapSRN with deep supervision using a robust Charbonnier ture the underlying multi-modal distributions of HR patches loss function and achieve high-quality reconstruction. Fur- (i.e., the same LR patch may have many corresponding HR thermore, our network generates multi-scale predictions in patches), the reconstructed HR images are often overly- one feed-forward pass through the progressive reconstruc- smooth and not close to human visual perception on nat- tion, thereby facilitates resource-aware applications. Ex- ural images. Third, most methods reconstruct HR images tensive quantitative and qualitative evaluations on bench- in one upsampling step, which increases the difficulties of mark datasets show that the proposed algorithm performs training for large scaling factors (e.g., 8×). In addition, ex- favorably against the state-of-the-art methods in terms of isting methods cannot generate intermediate SR predictions speed and accuracy. at multiple resolutions. As a result, one needs to train a large variety of models for various applications with differ- ent desired upsampling scales and computational loads. 1. Introduction To address these drawbacks, we propose the Laplacian Single-image super-resolution (SR) aims to reconstruct Pyramid Super-Resolution Network (LapSRN) based on a a high-resolution (HR) image from a single low-resolution cascade of convolutional neural networks (CNNs). Our net- (LR) input image. In recent years, example-based SR meth- work takes an LR image as input and progressively predicts ods have demonstrated the state-of-the-art performance by the sub-band residuals in a coarse-to-fine fashion. At each learning a mapping from LR to HR image patches using level, we first apply a cascade of convolutional layers to large image databases. Numerous learning algorithms have extract feature maps. We then use a transposed convolu- been applied to learn such a mapping, including dictionary tional layer for upsampling the feature maps to a finer level. learning [37, 38], local linear regression [30, 36], and ran- Finally, we use a convolutional layer to predict the sub- dom forest [26]. band residuals (the differences between the upsampled im- Recently, Dong et al. [7] propose a Super-Resolution age and the ground truth HR image at the respective level). Convolutional Neural Network (SRCNN) to learn a nonlin- The predicted residuals at each level are used to efficiently ear LR-to-HR mapping. The network is extended to embed reconstruct the HR image through upsampling and addi- a sparse coding-based network [33] or use a deeper struc- tion operations. While the proposed LapSRN consists of ture [17]. While these models demonstrate promising re- a set of cascaded sub-networks, we train the network with sults, there are three main issues. First, existing methods a robust Charbonnier loss function in an end-to-end fashion use a pre-defined upsampling operator, e.g., bicubic inter- (i.e., without stage-wise optimization). As depicted in Fig- 1 

2 . bicubic Feature Extraction Branch bicubic interpolation interpolation ... + ... ... ... (a) SRCNN [7] (c) VDSR [17] + bicubic + interpolation + ... Image Reconstruction Branch (b) FSRCNN [8] (d) DRCN [18] (e) LapSRN (ours) Figure 1: Network architectures of SRCNN [7], FSRCNN [8], VDSR [17], DRCN [18] and the proposed LapSRN. Red arrows indicate convolutional layers. Blue arrows indicate transposed convolutions (upsampling). Green arrows denote element-wise addition operators, and the orange arrow indicates recurrent layers. ure 1(e), our network architecture naturally accommodates 2. Related Work and Problem Context deep supervision (i.e., supervisory signals can be applied simultaneously at each level of the pyramid). Numerous single-image super-resolution methods have been proposed in the literature. Here we focus our discus- Our algorithm differs from existing CNN-based methods sion on recent example-based approaches. in the following three aspects: SR based on internal databases. Several methods [9, 12] exploit the self-similarity property in natural images and (1) Accuracy. The proposed LapSRN extracts feature maps construct LR-HR patch pairs based on the scale-space pyra- directly from LR images and jointly optimizes the upsam- mid of the low-resolution input image. While internal pling filters with deep convolutional layers to predict sub- databases contain more relevant training patches than ex- band residuals. The deep supervision with the Charbonnier ternal image databases, the number of LR-HR patch pairs loss improves the performance thanks to the ability to better may not be sufficient to cover large textural variations in an handle outliers. As a result, our model has a large capacity image. Singh et al. [29] decompose patches into directional to learn complicated mappings and effectively reduces the frequency sub-bands and determine better matches in each undesired visual artifacts. sub-band pyramid independently. Huang et al. [15] extend the patch search space to accommodate the affine transform (2) Speed. Our LapSRN embraces both fast processing and perspective deformation. The main drawback of SR speed and high capacity of deep networks. Experimen- methods based on internal databases is that they are typ- tal results demonstrate that our method is faster than sev- ically slow due to the heavy computational cost of patch eral CNN based super-resolution models, e.g., SRCNN [7], search in the scale-space pyramid. SCN [33], VDSR [17], and DRCN [18]. Similar to FSR- SR based on external databases. Numerous SR meth- CNN [8], our LapSRN achieves real-time speed on most ods learn the LR-HR mapping with image pairs collected of the evaluated datasets. In addition, our method provides from external databases using supervised learning algo- significantly better reconstruction accuracy. rithms, such as nearest neighbor [10], manifold embed- ding [2, 5], kernel ridge regression [19], and sparse rep- (3) Progressive reconstruction. Our model generates resentation [37, 38, 39]. Instead of directly modeling the multiple intermediate SR predictions in one feed-forward complex patch space over the entire database, several meth- pass through progressive reconstruction using the Laplacian ods partition the image database by K-means [36], sparse pyramid. This characteristic renders our technique applica- dictionary [30] or random forest [26], and learn locally lin- ble to a wide range of applications that require resource- ear regressors for each cluster. aware adaptability. For example, the same network can be Convolutional neural networks based SR. In contrast to used to enhance the spatial resolution of videos depend- modeling the LR-HR mapping in the patch space, SR- ing on the available computational resources. For scenar- CNN [7] jointly optimize all the steps and learn the non- ios with limited computing resources, our 8× model can linear mapping in the image space. The VDSR network [17] still perform 2× or 4× SR by simply bypassing the com- demonstrates significant improvement over SRCNN [7] by putation of residuals at finer levels. Existing CNN-based increasing the network depth from 3 to 20 convolutional methods, however, do not offer such flexibility. layers. To facilitate training a deeper model with a fast 2 

3 .Table 1: Comparisons of CNN based SR algorithms: SRCNN [7], FSRCNN [8], SCN [33], ESPCN [28], VDSR [17], and the proposed LapSRN. The number of layers includes both convolution and transposed convolution. Methods with direct reconstruction performs one-step upsampling (with bicubic interpolation or transposed convolution) from LR to HR images, while progressive reconstruction predicts HR images in multiple steps. Method Network input #Layers Residual learning Reconstruction Loss function SRCNN [7] LR + bicubic 3 No Direct L2 FSRCNN [8] LR 8 No Direct L2 SCN [33] LR + bicubic 5 No Progressive L2 ESPCN [28] LR 3 No Direct L2 VDSR [17] LR + bicubic 20 Yes Direct L2 DRCN [18] LR + bicubic 5 (recursive) No Direct L2 LapSRN (ours) LR 27 Yes Progressive Charbonnier convergence speed, VDSR trains the network to predict the tive model based on a Laplacian pyramid framework (LAP- residuals rather the actual pixel values. Wang et al. [33] GAN) to generate realistic images in [6], which is the most combine the domain knowledge of sparse coding with a related to our work. However, the proposed LapSRN differs deep CNN and train a cascade network (SCN) to up- from LAPGAN in three aspects. sample images to the desired scale factor progressively. First, LAPGAN is a generative model which is designed Kim et al. [18] propose a shallow network with deeply re- to synthesize diverse natural images from random noise and cursive layers (DRCN) to reduce the number of parameters. sample inputs. On the contrary, our LapSRN is a super- To achieve real-time performance, the ESPCN net- resolution model that predicts a particular HR image based work [28] extracts feature maps in the LR space and re- on the given LR image. LAPGAN uses a cross-entropy loss places the bicubic upsampling operation with an efficient function to encourage the output images to respect the data sub-pixel convolution. The FSRCNN network [8] adopts a distribution of training datasets. In contrast, we use the similar idea and uses a hourglass-shaped CNN with more Charbonnier penalty function to penalize the deviation of layers but fewer parameters than that in ESPCN. All the the prediction from the ground truth sub-band residuals. above CNN-based SR methods optimize networks with an Second, the sub-networks of LAPGAN are independent 2 loss function, which often leads to overly-smooth results (i.e., no weight sharing). As a result, the network capacity that do not correlate well with human perception. In the is limited by the depth of each sub-network. Unlike LAP- context of SR, we demonstrate that the 2 loss is less effec- GAN, the convolutional layers at each level in LapSRN are tive for learning and predicting sparse residuals. connected through multi-channel transposed convolutional We compare the network structures of SRCNN, FSR- layers. The residual images at a higher level are therefore CNN, VDSR, DRCN and our LapSRN in Figure 1 and predicted by a deeper network with shared feature represen- list the main differences among existing CNN-based meth- tations at lower levels. The feature sharing at lower levels ods and the proposed framework in Table 1. Our approach increases the non-linearity at finer convolutional layers to builds upon existing CNN-based SR algorithms with three learn complex mappings. Also, the sub-networks in LAP- main differences. First, we jointly learn residuals and up- GAN are independently trained. On the other hand, all the sampling filters with convolutional and transposed convo- convolutional filters for feature extraction, upsampling, and lutional layers. Using the learned upsampling filters not residual prediction layers in the LapSRN are jointly trained only effectively suppresses reconstruction artifacts caused in an end-to-end, deeply supervised fashion. by the bicubic interpolation, but also dramatically reduces Third, LAPGAN applies convolutions on the upsampled the computational complexity. Second, we optimize the images, so the speed depends on the size of HR images. On deep network using a robust Charbonnier loss function in- the contrary, our design of LapSRN effectively increases stead of the 2 loss to handle outliers and improve the re- the size of the receptive field and accelerates the speed by construction accuracy. Third, as the proposed LapSRN pro- extracting features from the LR space. We provide compar- gressively reconstructs HR images, the same model can be isons with LAPGAN in the supplementary material. used for applications that require different scale factors by Adversarial training. The SRGAN method [20] optimizes truncating the network up to a certain level. the network using the perceptual loss [16] and the adversar- Laplacian pyramid. The Laplacian pyramid has been used ial loss for photo-realistic SR. We note that our LapSRN can in a wide range of applications, such as image blending [4], be easily extended to the adversarial training framework. As texture synthesis [14], edge-aware filtering [24] and seman- it is not our contribution, we provide experiments on the ad- tic segmentation [11, 25]. Denton et al. propose a genera- versarial loss in the supplementary material. 3 

4 .3. Deep Laplacian Pyramid Network for SR by ys = xs + rs . We use the bicubic downsampling to resize In this section, we describe the design methodology of the ground truth HR image y to ys at each level. Instead of the proposed Laplacian pyramid network, the optimization minimizing the mean square errors between ys and yˆs , we using robust loss functions with deep supervision, and the propose to use a robust loss function to handle outliers. The details for network training. overall loss function is defined as: 1 N L (i) (i) 3.1. Network architecture L (y, ˆ y; θ ) = ∑ ∑ ρ yˆs − ys N i=1 s=1 We propose to construct our network based on the Lapla- cian pyramid framework, as shown in Figure 1(e). Our 1 N L (i) (i) (i) model takes an LR image as input (rather than an upscaled = ∑ ∑ ρ (yˆs − xs ) − rs , N i=1 (1) s=1 version of the LR image) and progressively predicts resid- √ where ρ(x) = x2 + ε 2 is the Charbonnier penalty function ual images at log2 S levels where S is the scale factor. For (a differentiable variant of 1 norm) [3], N is the number of example, the network consists of 3 sub-networks for super- training samples in each batch, and L is the number of level resolving an LR image at a scale factor of 8. Our model has in our pyramid. We empirically set ε to 1e − 3. two branches: (1) feature extraction and (2) image recon- In the proposed LapSRN, each level s has its loss func- struction. tion and the corresponding ground truth HR image ys . This Feature extraction. At level s, the feature extraction multi-loss structure resembles the deeply-supervised nets branch consists of d convolutional layers and one trans- for classification [21] and edge detection [34]. However, posed convolutional layer to upsample the extracted fea- the labels used to supervise intermediate layers in [21, 34] tures by a scale of 2. The output of each transposed con- are the same across the networks. In our model, we use volutional layer is connected to two different layers: (1) a different scales of HR images at the corresponding level as convolutional layer for reconstructing a residual image at supervision. The deep supervision guides the network train- level s, and (2) a convolutional layer for extracting features ing to predict sub-band residual images at different levels at the finer level s + 1. Note that we perform the feature ex- and produce multi-scale output images. For example, our traction at the coarse resolution and generate feature maps 8× model can produce 2×, 4× and 8× super-resolution re- at the finer resolution with only one transposed convolu- sults in one feed-forward pass. This property is particularly tional layer. In contrast to existing networks that perform all useful for resource-aware applications, e.g., mobile devices feature extraction and reconstruction at the fine resolution, or network applications. our network design significantly reduces the computational complexity. Note that the feature representations at lower 3.3. Implementation and training details levels are shared with higher levels, and thus can increase In the proposed LapSRN, each convolutional layer con- the non-linearity of the network to learn complex mappings sists of 64 filters with the size of 3 × 3. We initialize the at the finer levels. convolutional filters using the method of He et al. [13]. The Image reconstruction. At level s, the input image is up- size of the transposed convolutional filters is 4 × 4 and the sampled by a scale of 2 with a transposed convolutional weights are initialized from a bilinear filter. All the con- (upsampling) layer. We initialize this layer with the bi- volutional and transposed convolutional layers (except the linear kernel and allow it to be jointly optimized with all reconstruction layers) are followed by leaky rectified linear the other layers. The upsampled image is then combined units (LReLUs) with a negative slope of 0.2. We pad zeros (using element-wise summation) with the predicted resid- around the boundaries before applying convolution to keep ual image from the feature extraction branch to produce a the size of all feature maps the same as the input of each high-resolution output image. The output HR image at level level. The convolutional filters have small spatial supports s is then fed into the image reconstruction branch of level (3 × 3). However, we can achieve high non-linearity and s + 1. The entire network is a cascade of CNNs with a sim- increase the size of receptive fields with a deep structure. ilar structure at each level. We use 91 images from Yang et al. [38] and 200 images from the training set of Berkeley Segmentation Dataset [1] 3.2. Loss function as our training data. The same training dataset is used Let x be the input LR image and θ be the set of net- in [17, 26] as well. In each training batch, we randomly work parameters to be optimized. Our goal is to learn a sample 64 patches with the size of 128 × 128. An epoch mapping function f for generating a high-resolution im- has 1, 000 iterations of back-propagation. We augment the age yˆ = f (x; θ ) that is close to the ground truth HR image training data in three ways: (1) Scaling: randomly down- y. We denote the residual image at level s by rs , the up- scale between [0.5, 1.0]. (2) Rotation: randomly rotate im- scaled LR image by xs and the corresponding HR images age by 90◦ , 180◦ , or 270◦ . (3) Flipping: flip images hor- by ys . The desired output HR images at level s is modeled izontally or vertically with a probability of 0.5. Following 4 

5 . 28.2 27.8 PSNR (dB) 27.4 SRCNN FSRCNN (a) (b) (c) (d) (e) (f) w/o pyramid structure 27 w/o residual learning Figure 3: Contribution of different components in the pro- w/o robust loss LapSRN (full model) posed network. (a) HR image. (b) w/o pyramid structure 26.6 (c) w/o residual learning (d) w/o robust loss (e) full model 0 50 100 150 Epoch (f) ground truth. Figure 2: Convergence analysis on the pyramid structure, Table 3: Trade-off between performance and speed on the loss functions and residual learning. Our LapSRN con- depth at each level of the proposed network. verges faster and achieves improved performance. S ET 5 S ET 14 Depth Table 2: Ablation study of pyramid structures, loss func- PSNR Second PSNR Second tions, and residual learning. We replace each component 3 31.15 0.036 27.98 0.036 with the one used in existing methods, and observe perfor- 5 31.28 0.044 28.04 0.042 mance (PSNR) drop on both S ET 5 and S ET 14. 10 31.37 0.050 28.11 0.051 Residual Pyramid Loss S ET 5 S ET 14 15 31.45 0.077 28.16 0.071 Robust 30.58 27.61 curve) requires more iterations to achieve comparable per- Robust 31.10 27.94 formance with SRCNN. In Figure 3(d), we show that the 2 30.93 27.86 network trained with the 2 loss generates SR results with Robust 31.28 28.04 more ringing artifacts. In contrast, the SR images recon- struct by the proposed algorithm (Figure 3(e)) contain rela- the protocol of existing methods [7, 17], we generate the LR tively clean and sharp details. training patches using the bicubic downsampling. We train Pyramid structure. By removing the pyramid structure, our model with the MatConvNet toolbox [31]. We set mo- our model falls back to a network similar to FSRCNN but mentum parameter to 0.9 and the weight decay to 1e − 4. with the residual learning. To use the same number of The learning rate is initialized to 1e − 5 for all layers and convolutional layers as LapSRN, we train a network with decreased by a factor of 2 for every 50 epochs. 10 convolutional layers and one transposed convolutional layer. The quantitative results in Table 2 shows that the 4. Experiment Results pyramid structure leads to moderate performance improve- We first analyze the contributions of different compo- ment (e.g. 0.7 dB on S ET 5 and 0.4 dB on S ET 14). nents of the proposed network. We then compare our Lap- Network depth. We train the proposed model with differ- SRN with state-of-the-art algorithms on five benchmark ent depth, d = 3, 5, 10, 15, at each level and show the trade- datasets and demonstrate the applications of our method on offs between performance and speed in Table 3. In general, super-resolving real-world photos and videos. deep networks perform better shallow ones at the expense of increased computational cost. We choose d = 10 for our 4.1. Model analysis 2× and 4× SR models to strike a balance between perfor- Residual learning. To demonstrate the effect of residual mance and speed. We show that the speed of our LapSRN learning, we remove the image reconstruction branch and with d = 10 is faster than most of the existing CNN-based directly predict the HR images at each level. Figure 2 shows SR algorithms (see Figure 6). For 8× model, we choose the convergence curves in terms of PSNR on the S ET 14 d = 5 because we do not observe significant performance for 4× SR. The performance of the “non-residual” network gain by using more convolutional layers. (blue curve) converges slowly and fluctuates significantly. 4.2. Comparisons with the state-of-the-arts The proposed LapSRN (red curve), on the other hand, out- performs SRCNN within 10 epochs. We compare the proposed LapSRN with 8 state-of-the- Loss function. To validate the effect of the Charbonnier art SR algorithms: A+ [30], SRCNN [7], FSRCNN [8], loss function, we train the proposed network with the 2 SelfExSR [15], RFL [26], SCN [33], VDSR [17] and loss function. We use a larger learning rate (1e − 4) since DRCN [18]. We carry out extensive experiments using the gradient magnitude of the 2 loss is smaller. As illus- 5 datasets: S ET 5 [2], S ET 14 [39], BSDS100 [1], U R - trated in Figure 2, the network optimized with 2 loss (green BAN 100 [15] and MANGA 109 [23]. Among these datasets, 5 

6 . HR (PSNR, SSIM) Bicubic (24.76, 0.6633) A+ [30] (25.59, 0.7139) SelfExSR [15] (25.45, 0.7087) Ground-truth HR FSRCNN [8] (25.81, 0.7248) VDSR [17] (25.94, 0.7353) DRCN [18] (25.98, 0.7357) Ours (26.09, 0.7403) HR (PSNR, SSIM) Bicubic (22.43, 0.5926) A+ [30] (23.19, 0.6545) SelfExSR [15] (23.88, 0.6961) Ground-truth HR FSRCNN [8] (23.61, 0.6708) VDSR [17] (24.25, 0.7030) DRCN [18] (23.95, 0.6947) Ours (24.36, 0.7200) HR (PSNR, SSIM) Bicubic (23.53, 0.8073) A+ [30] (26.10, 0.8793) SelfExSR [15] (26.75, 0.8960) Ground-truth HR FSRCNN [8] (27.19, 0.8896) VDSR [17] (27.99, 0.9202) DRCN [18] (28.18, 0.9218) Ours (28.25, 0.9224) Figure 4: Visual comparison for 4× SR on BSDS100, U RBAN 100 and M ANGA 109. HR FSRCNN [8] HR FSRCNN [8] (PSNR, SSIM) (19.57, 0.5133) (PSNR, SSIM) (15.61, 0.3494) Ground-truth HR VDSR [17] LapSRN (ours) Ground-truth HR VDSR [17] LapSRN (ours) (19.58, 0.5147) (19.75, 0.5246) (15.66, 0.3644) (15.72, 0.3865) Figure 5: Visual comparison for 8× SR on BSDS100 and U RBAN 100. S ET 5, S ET 14 and BSDS100 consist of natural scenes; U R - intermediate convolutional layers are trained to minimize BAN 100 contains challenging urban scenes images with the prediction errors for both the corresponding level and details in different frequency bands; and MANGA 109 is a higher levels, the intermediate predictions of our 8× model dataset of Japanese manga. We train the LapSRN until the are slightly inferior to our 2× and 4× models. Neverthe- learning rate decreases to 1e − 6 and the training time is less, our 8× model provides a competitive performance to around three days on a Titan X GPU. the state-of-the-art methods in 2× and 4× SR. We evaluate the SR images with three commonly used In Figure 4, we show visual comparisons on U RBAN 100, image quality metrics: PSNR, SSIM [32], and IFC [27]. BSDS100 and M ANGA 109 with the a scale factor of Table 4 shows quantitative comparisons for 2×, 4× and 8× 4×. Our method accurately reconstructs parallel straight SR. Our LapSRN performs favorably against existing meth- lines and grid patterns such as windows and the stripes on ods on most datasets. In particular, our algorithm achieves tigers. We observe that methods using the bicubic upsam- higher IFC values, which has been shown to be correlated pling for pre-processing generate results with noticeable ar- well with human perception of image super-resolution [35]. tifacts [7, 17, 26, 30, 33]. In contrast, our approach effec- We note that the best results can be achieved by training tively suppresses such artifacts through progressive recon- with specific scale factors (Ours 2× and Ours 4×). As the struction and the robust loss function. 6 

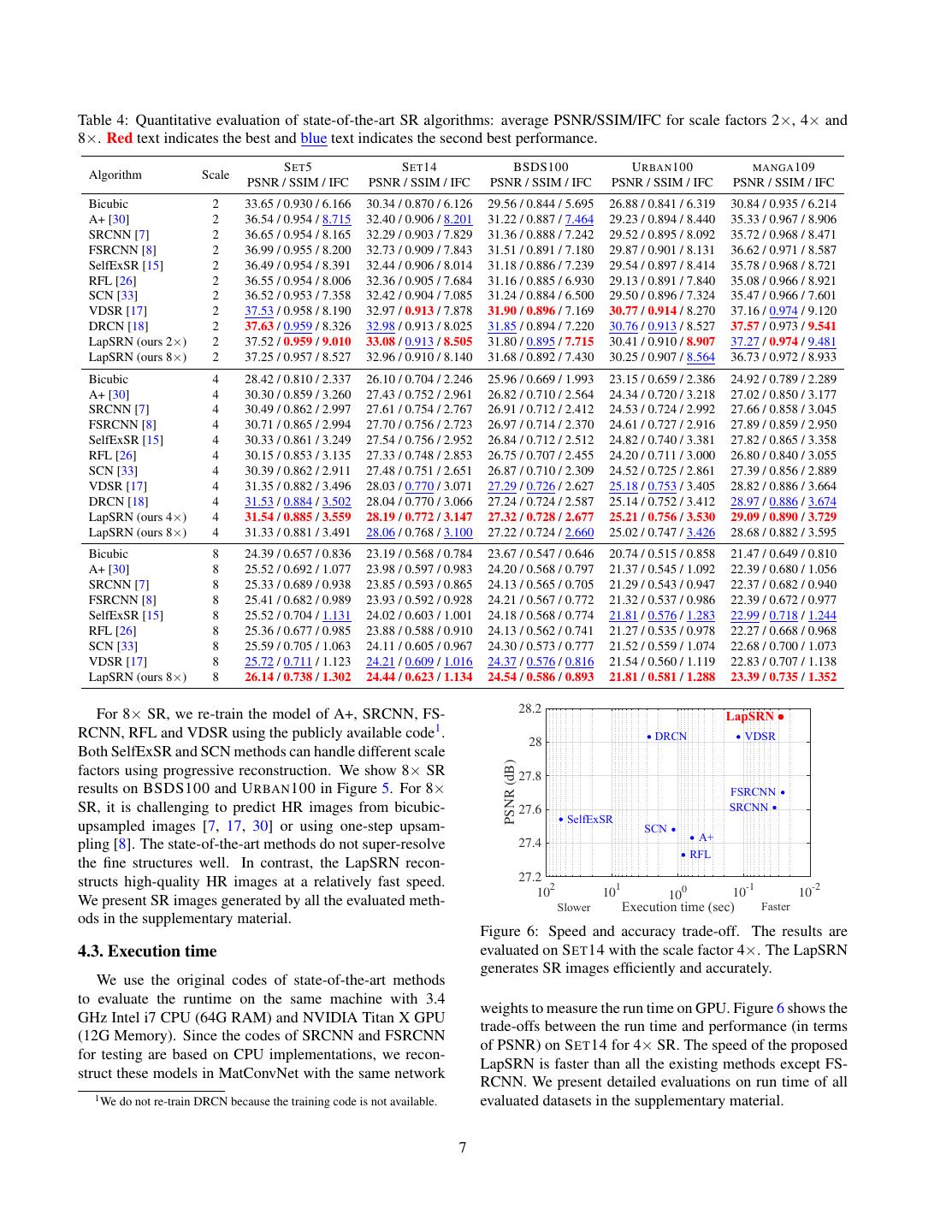
7 .Table 4: Quantitative evaluation of state-of-the-art SR algorithms: average PSNR/SSIM/IFC for scale factors 2×, 4× and 8×. Red text indicates the best and blue text indicates the second best performance. S ET 5 S ET 14 BSDS100 U RBAN 100 MANGA 109 Algorithm Scale PSNR / SSIM / IFC PSNR / SSIM / IFC PSNR / SSIM / IFC PSNR / SSIM / IFC PSNR / SSIM / IFC Bicubic 2 33.65 / 0.930 / 6.166 30.34 / 0.870 / 6.126 29.56 / 0.844 / 5.695 26.88 / 0.841 / 6.319 30.84 / 0.935 / 6.214 A+ [30] 2 36.54 / 0.954 / 8.715 32.40 / 0.906 / 8.201 31.22 / 0.887 / 7.464 29.23 / 0.894 / 8.440 35.33 / 0.967 / 8.906 SRCNN [7] 2 36.65 / 0.954 / 8.165 32.29 / 0.903 / 7.829 31.36 / 0.888 / 7.242 29.52 / 0.895 / 8.092 35.72 / 0.968 / 8.471 FSRCNN [8] 2 36.99 / 0.955 / 8.200 32.73 / 0.909 / 7.843 31.51 / 0.891 / 7.180 29.87 / 0.901 / 8.131 36.62 / 0.971 / 8.587 SelfExSR [15] 2 36.49 / 0.954 / 8.391 32.44 / 0.906 / 8.014 31.18 / 0.886 / 7.239 29.54 / 0.897 / 8.414 35.78 / 0.968 / 8.721 RFL [26] 2 36.55 / 0.954 / 8.006 32.36 / 0.905 / 7.684 31.16 / 0.885 / 6.930 29.13 / 0.891 / 7.840 35.08 / 0.966 / 8.921 SCN [33] 2 36.52 / 0.953 / 7.358 32.42 / 0.904 / 7.085 31.24 / 0.884 / 6.500 29.50 / 0.896 / 7.324 35.47 / 0.966 / 7.601 VDSR [17] 2 37.53 / 0.958 / 8.190 32.97 / 0.913 / 7.878 31.90 / 0.896 / 7.169 30.77 / 0.914 / 8.270 37.16 / 0.974 / 9.120 DRCN [18] 2 37.63 / 0.959 / 8.326 32.98 / 0.913 / 8.025 31.85 / 0.894 / 7.220 30.76 / 0.913 / 8.527 37.57 / 0.973 / 9.541 LapSRN (ours 2×) 2 37.52 / 0.959 / 9.010 33.08 / 0.913 / 8.505 31.80 / 0.895 / 7.715 30.41 / 0.910 / 8.907 37.27 / 0.974 / 9.481 LapSRN (ours 8×) 2 37.25 / 0.957 / 8.527 32.96 / 0.910 / 8.140 31.68 / 0.892 / 7.430 30.25 / 0.907 / 8.564 36.73 / 0.972 / 8.933 Bicubic 4 28.42 / 0.810 / 2.337 26.10 / 0.704 / 2.246 25.96 / 0.669 / 1.993 23.15 / 0.659 / 2.386 24.92 / 0.789 / 2.289 A+ [30] 4 30.30 / 0.859 / 3.260 27.43 / 0.752 / 2.961 26.82 / 0.710 / 2.564 24.34 / 0.720 / 3.218 27.02 / 0.850 / 3.177 SRCNN [7] 4 30.49 / 0.862 / 2.997 27.61 / 0.754 / 2.767 26.91 / 0.712 / 2.412 24.53 / 0.724 / 2.992 27.66 / 0.858 / 3.045 FSRCNN [8] 4 30.71 / 0.865 / 2.994 27.70 / 0.756 / 2.723 26.97 / 0.714 / 2.370 24.61 / 0.727 / 2.916 27.89 / 0.859 / 2.950 SelfExSR [15] 4 30.33 / 0.861 / 3.249 27.54 / 0.756 / 2.952 26.84 / 0.712 / 2.512 24.82 / 0.740 / 3.381 27.82 / 0.865 / 3.358 RFL [26] 4 30.15 / 0.853 / 3.135 27.33 / 0.748 / 2.853 26.75 / 0.707 / 2.455 24.20 / 0.711 / 3.000 26.80 / 0.840 / 3.055 SCN [33] 4 30.39 / 0.862 / 2.911 27.48 / 0.751 / 2.651 26.87 / 0.710 / 2.309 24.52 / 0.725 / 2.861 27.39 / 0.856 / 2.889 VDSR [17] 4 31.35 / 0.882 / 3.496 28.03 / 0.770 / 3.071 27.29 / 0.726 / 2.627 25.18 / 0.753 / 3.405 28.82 / 0.886 / 3.664 DRCN [18] 4 31.53 / 0.884 / 3.502 28.04 / 0.770 / 3.066 27.24 / 0.724 / 2.587 25.14 / 0.752 / 3.412 28.97 / 0.886 / 3.674 LapSRN (ours 4×) 4 31.54 / 0.885 / 3.559 28.19 / 0.772 / 3.147 27.32 / 0.728 / 2.677 25.21 / 0.756 / 3.530 29.09 / 0.890 / 3.729 LapSRN (ours 8×) 4 31.33 / 0.881 / 3.491 28.06 / 0.768 / 3.100 27.22 / 0.724 / 2.660 25.02 / 0.747 / 3.426 28.68 / 0.882 / 3.595 Bicubic 8 24.39 / 0.657 / 0.836 23.19 / 0.568 / 0.784 23.67 / 0.547 / 0.646 20.74 / 0.515 / 0.858 21.47 / 0.649 / 0.810 A+ [30] 8 25.52 / 0.692 / 1.077 23.98 / 0.597 / 0.983 24.20 / 0.568 / 0.797 21.37 / 0.545 / 1.092 22.39 / 0.680 / 1.056 SRCNN [7] 8 25.33 / 0.689 / 0.938 23.85 / 0.593 / 0.865 24.13 / 0.565 / 0.705 21.29 / 0.543 / 0.947 22.37 / 0.682 / 0.940 FSRCNN [8] 8 25.41 / 0.682 / 0.989 23.93 / 0.592 / 0.928 24.21 / 0.567 / 0.772 21.32 / 0.537 / 0.986 22.39 / 0.672 / 0.977 SelfExSR [15] 8 25.52 / 0.704 / 1.131 24.02 / 0.603 / 1.001 24.18 / 0.568 / 0.774 21.81 / 0.576 / 1.283 22.99 / 0.718 / 1.244 RFL [26] 8 25.36 / 0.677 / 0.985 23.88 / 0.588 / 0.910 24.13 / 0.562 / 0.741 21.27 / 0.535 / 0.978 22.27 / 0.668 / 0.968 SCN [33] 8 25.59 / 0.705 / 1.063 24.11 / 0.605 / 0.967 24.30 / 0.573 / 0.777 21.52 / 0.559 / 1.074 22.68 / 0.700 / 1.073 VDSR [17] 8 25.72 / 0.711 / 1.123 24.21 / 0.609 / 1.016 24.37 / 0.576 / 0.816 21.54 / 0.560 / 1.119 22.83 / 0.707 / 1.138 LapSRN (ours 8×) 8 26.14 / 0.738 / 1.302 24.44 / 0.623 / 1.134 24.54 / 0.586 / 0.893 21.81 / 0.581 / 1.288 23.39 / 0.735 / 1.352 28.2 For 8× SR, we re-train the model of A+, SRCNN, FS- LapSRN RCNN, RFL and VDSR using the publicly available code1 . DRCN VDSR 28 Both SelfExSR and SCN methods can handle different scale PSNR (dB) factors using progressive reconstruction. We show 8× SR 27.8 results on BSDS100 and U RBAN 100 in Figure 5. For 8× FSRCNN SR, it is challenging to predict HR images from bicubic- 27.6 SRCNN SelfExSR upsampled images [7, 17, 30] or using one-step upsam- SCN 27.4 A+ pling [8]. The state-of-the-art methods do not super-resolve RFL the fine structures well. In contrast, the LapSRN recon- structs high-quality HR images at a relatively fast speed. 27.2 102 101 100 10-1 10-2 We present SR images generated by all the evaluated meth- Slower Execution time (sec) Faster ods in the supplementary material. Figure 6: Speed and accuracy trade-off. The results are 4.3. Execution time evaluated on S ET 14 with the scale factor 4×. The LapSRN generates SR images efficiently and accurately. We use the original codes of state-of-the-art methods to evaluate the runtime on the same machine with 3.4 weights to measure the run time on GPU. Figure 6 shows the GHz Intel i7 CPU (64G RAM) and NVIDIA Titan X GPU trade-offs between the run time and performance (in terms (12G Memory). Since the codes of SRCNN and FSRCNN of PSNR) on S ET 14 for 4× SR. The speed of the proposed for testing are based on CPU implementations, we recon- LapSRN is faster than all the existing methods except FS- struct these models in MatConvNet with the same network RCNN. We present detailed evaluations on run time of all 1 We do not re-train DRCN because the training code is not available. evaluated datasets in the supplementary material. 7 

8 . Bicubic FSRCNN [8] Bicubic FSRCNN [8] Ground-truth HR VDSR [17] LapSRN (ours) Ground-truth HR VDSR [17] LapSRN (ours) Figure 7: Comparison of real-world photos for 4× SR. We note that the ground truth HR images and the blur kernels are not available in these cases. On the left image, our method super-resolves the letter “W” accurately while VDSR incorrectly connects the stroke with the letter “O”. On the right image, our method reconstructs the rails without the ringing artifacts. HR SRCNN [7] HR SelfExSR [15] Ground-truth HR VDSR [17] LapSRN (ours) Ground-truth HR VDSR [17] LapSRN (ours) Figure 8: Visual comparison on a video frame with a spatial Figure 9: A failure case for 8× SR. Our method is not able resolution of 1200 × 800 for 8× SR. Our method provides to hallucinate details if the LR input image does not consist more clean and sharper results than existing methods. of sufficient amount of structure. 4.4. Super-resolving real-world photos image. All SR algorithms fail to recover the fine structure except SelfExSR [15], which explicitly detects the 3D scene We demonstrate an application of super-resolving his- geometry and uses self-similarity to hallucinate the regular torical photographs with JPEG compression artifacts. In structure. This is a common limitation shared by paramet- these cases, neither the ground-truth images nor the down- ric SR methods [7, 8, 17, 18]. Another limitation of the sampling kernels are available. As shown in Figure 7, our proposed network is the relative large model size. To re- method can reconstruct sharper and more accurate images duce the number of parameters, one can replace the deep than the state-of-the-art approaches. convolutional layers at each level with recursive layers. 4.5. Super-resolving video sequences 5. Conclusions We conduct frame-based SR experiments on two video sequences from [22] with a spatial resolution of 1200 × 800 In this work, we propose a deep convolutional network pixels.2 We downsample each frame by 8×, and then ap- within a Laplacian pyramid framework for fast and ac- ply super-resolution frame by frame for 2×, 4× and 8×, curate single-image super-resolution. Our model progres- respectively. The computational cost depends on the size of sively predicts high-frequency residuals in a coarse-to-fine input images since we extract features from the LR space. manner. By replacing the pre-defined bicubic interpolation On the contrary, the speed of SRCNN and VDSR is limited with the learned transposed convolutional layers and opti- by the size of output images. Both FSRCNN and our ap- mizing the network with a robust loss function, the pro- proach achieve real-time performance (i.e., over 30 frames posed LapSRN alleviates issues with undesired artifacts and per second) on all upsampling scales. In contrast, the FPS reduces the computational complexity. Extensive evalua- is 8.43 for SRCNN and 1.98 for VDSR on 8× SR. Figure 8 tions on benchmark datasets demonstrate that the proposed visualizes results of 8× SR on one representative frame. model performs favorably against the state-of-the-art SR al- gorithms in terms of visual quality and run time. 4.6. Limitations Acknowledgments While our model is capable of generating clean and sharp HR images on a large scale factor, e.g., 8×, it does not “hal- This work is supported in part by the NSF CAREER lucinate” fine details. As shown in Figure 9, the top of the Grant #1149783, gifts from Adobe and Nvidia. J.-B. Huang building is significantly blurred in the 8× downscaled LR and N. Ahuja are supported in part by Office of Naval Re- search under Grant N00014-16-1-2314. 2 Our method is not a video super-resolution algorithm as temporal co- herence or motion blur are not considered. 8 

9 .References [20] C. Ledig, L. Theis, F. Huszar, J. Caballero, A. Cunning- ham, A. Acosta, A. Aitken, A. Tejani, J. Totz, Z. Wang, and [1] P. Arbelaez, M. Maire, C. Fowlkes, and J. Malik. Con- W. Shi. Photo-realistic single image super-resolution using a tour detection and hierarchical image segmentation. TPAMI, generative adversarial network. In CVPR, 2017. 3 33(5):898–916, 2011. 4, 5 [21] C. Lee, S. Xie, P. Gallagher, Z. Zhang, and Z. Tu. Deeply- [2] M. Bevilacqua, A. Roumy, C. Guillemot, and M. L. Alberi- supervised nets, 2015. In International Conference on Arti- Morel. Low-complexity single-image super-resolution based ficial Intelligence and Statistics, 2015. 4 on nonnegative neighbor embedding. In BMVC, 2012. 2, 5 [22] R. Liao, X. Tao, R. Li, Z. Ma, and J. Jia. Video super- [3] A. Bruhn, J. Weickert, and C. Schn¨orr. Lucas/Kanade meets resolution via deep draft-ensemble learning. In ICCV, 2015. Horn/Schunck: Combining local and global optic flow meth- 8 ods. IJCV, 61(3):211–231, 2005. 4 [23] Y. Matsui, K. Ito, Y. Aramaki, T. Yamasaki, and K. Aizawa. [4] P. J. Burt and E. H. Adelson. The Laplacian pyramid as a Sketch-based manga retrieval using manga109 dataset. Mul- compact image code. IEEE Transactions on Communica- timedia Tools and Applications, pages 1–28, 2016. 5 tions, 31(4):532–540, 1983. 3 [24] S. Paris, S. W. Hasinoff, and J. Kautz. Local laplacian fil- [5] H. Chang, D.-Y. Yeung, and Y. Xiong. Super-resolution ters: Edge-aware image processing with a laplacian pyramid. through neighbor embedding. In CVPR, 2004. 2 ACM TOG (Proc. of SIGGRAPH), 30(4):68, 2011. 3 [6] E. L. Denton, S. Chintala, and R. Fergus. Deep generative [25] P. O. Pinheiro, T.-Y. Lin, R. Collobert, and P. Doll´ar. Learn- image models using a laplacian pyramid of adversarial net- ing to refine object segments. In ECCV, 2016. 3 works. In NIPS, 2015. 3 [26] S. Schulter, C. Leistner, and H. Bischof. Fast and accu- [7] C. Dong, C. C. Loy, K. He, and X. Tang. Image super- rate image upscaling with super-resolution forests. In CVPR, resolution using deep convolutional networks. TPAMI, 2015. 1, 2, 4, 5, 6, 7 38(2):295–307, 2015. 1, 2, 3, 5, 6, 7, 8 [27] H. R. Sheikh, A. C. Bovik, and G. De Veciana. An infor- [8] C. Dong, C. C. Loy, and X. Tang. Accelerating the super- mation fidelity criterion for image quality assessment using resolution convolutional neural network. In ECCV, 2016. 1, natural scene statistics. TIP, 14(12):2117–2128, 2005. 6 2, 3, 5, 6, 7, 8 [28] W. Shi, J. Caballero, F. Huszar, J. Totz, A. Aitken, R. Bishop, [9] G. Freedman and R. Fattal. Image and video upscaling D. Rueckert, and Z. Wang. Real-time single image and video from local self-examples. ACM TOG (Proc. of SIGGRAPH), super-resolution using an efficient sub-pixel convolutional 30(2):12, 2011. 2 neural network. In CVPR, 2016. 1, 3 [10] W. T. Freeman, T. R. Jones, and E. C. Pasztor. Example- [29] A. Singh and N. Ahuja. Super-resolution using sub-band based super-resolution. IEEE, Computer Graphics and Ap- self-similarity. In ACCV, 2014. 2 plications, 22(2):56–65, 2002. 2 [30] R. Timofte, V. De Smet, and L. Van Gool. A+: Adjusted [11] G. Ghiasi and C. C. Fowlkes. Laplacian pyramid reconstruc- anchored neighborhood regression for fast super-resolution. tion and refinement for semantic segmentation. In ECCV, In ACCV, 2014. 1, 2, 5, 6, 7 2016. 3 [31] A. Vedaldi and K. Lenc. MatConvNet: Convolutional neural [12] D. Glasner, S. Bagon, and M. Irani. Super-resolution from a networks for matlab. In ACM MM, 2015. 5 single image. In ICCV, 2009. 2 [32] Z. Wang, A. C. Bovik, H. R. Sheikh, and E. P. Simoncelli. [13] K. He, X. Zhang, S. Ren, and J. Sun. Delving deep into Image quality assessment: From error visibility to structural rectifiers: Surpassing human-level performance on imagenet similarity. TIP, 13(4):600–612, 2004. 6 classification. In ICCV, 2015. 4 [33] Z. Wang, D. Liu, J. Yang, W. Han, and T. Huang. Deep networks for image super-resolution with sparse prior. In [14] D. J. Heeger and J. R. Bergen. Pyramid-based texture analy- ICCV, 2015. 1, 2, 3, 5, 6, 7 sis/synthesis. In SIGGRAPH, 1995. 3 [34] S. Xie and Z. Tu. Holistically-nested edge detection. In [15] J.-B. Huang, A. Singh, and N. Ahuja. Single image super- CVPR, 2015. 4 resolution from transformed self-exemplars. In CVPR, 2015. [35] C.-Y. Yang, C. Ma, and M.-H. Yang. Single-image super- 2, 5, 6, 7, 8 resolution: a benchmark. In ECCV. 2014. 6 [16] J. Johnson, A. Alahi, and L. Fei-Fei. Perceptual losses for [36] C.-Y. Yang and M.-H. Yang. Fast direct super-resolution by real-time style transfer and super-resolution. In ECCV, 2016. simple functions. In ICCV, 2013. 1, 2 3 [37] J. Yang, J. Wright, T. Huang, and Y. Ma. Image super- [17] J. Kim, J. K. Lee, and K. M. Lee. Accurate image super- resolution as sparse representation of raw image patches. In resolution using very deep convolutional networks. In CVPR, CVPR, 2008. 1, 2 2016. 1, 2, 3, 4, 5, 6, 7, 8 [38] J. Yang, J. Wright, T. S. Huang, and Y. Ma. Image super- [18] J. Kim, J. K. Lee, and K. M. Lee. Deeply-recursive convolu- resolution via sparse representation. TIP, 19(11):2861–2873, tional network for image super-resolution. In CVPR, 2016. 2010. 1, 2, 4 2, 3, 5, 6, 7, 8 [39] R. Zeyde, M. Elad, and M. Protter. On single image scale-up [19] K. I. Kim and Y. Kwon. Single-image super-resolution using sparse-representations. In Curves and Surfaces. 2010. using sparse regression and natural image prior. TPAMI, 2, 5 32(6):1127–1133, 2010. 2 9