05_More LISP Examples. Genetic Algorithm

1 . Example of formula (defun roots (a b c) (list (/ (+ (- b) (sqrt (- (expt b 2) (* 4 a c)) )) (* 2 a)) (/ (+ (- b) (sqrt (- (expt b 2) (* 4 a c)) )) (* 2 a)) )) Returns a list of solutions to a quadratic equation 

2 . eval and quote > (eval (cdr '(a + 2 3))) 5 > (setq a 'b) b > a b > b error: unbound variable - b if continued: try evaluating symbol again 1> [ back to top level ] > (set 'a 'b) Value of atom a b is atom b > (eval (eval ''a)) b For every quote > 'a there is an eval a 

3 . eval and quote For every quote > (eval (eval '(quote a))) there is an eval b > 'a a > (eval '(list '* 9 6)) (* 9 6) > (eval (eval '(list * 9 6))) error: bad function - (* 9 6) 1> [ back to top level ] > (eval (eval '(list '* 9 6))) 54 

4 . Examples of tail recursion • If last operation in function is recursive call, overwrite actuals and go to beginning of code: (defun last (lis) ; finds the last element of the list (if (null? (cdr lis) (car lis)) (last (crd lis)))) ; can be done with loop (defun length (lis) ; calculates the length of the list (if (null? lis) 0) (+ 1 (length (cdr lis)))) ; not tail recursive! 

5 . Example of Tree Recursion: Fibonacci • Writing a function to compute the nth Fibonacci number – Fibonacci sequence: 0, 1, 1, 2, 3, 5, 8, 13, … • fib(0) = 0 • fib(1) = 1 • fib(n) = fib(n-2) + fib(n-1) 

6 . Short Version of tree recursion (defun fib (n) (cond ((eql n 0) 0) ; base case ((eql n 1) 1) ; base case (t (+ (fib (- n 1)) ; recursively compute fib(n) (fib (- n 2)))))) 

7 . Complete Version with Error Checking and Comments (defun fib (n) "Computes the nth Fibonacci number." (cond ((or (not (integerp n)) (< n 0)) ; error case (error "~s must be an integer >= 0.~&" n)) ((eql n 0) 0) ; base case ((eql n 1) 1) ; base case (t (+ (fib (- n 1)) ; recursively compute fib(n) (fib (- n 2)))))) 

8 . Problems: 1. Write a function (power 3 2) = 3^2 = 9 2. Write a function that counts the number of atoms in an expression. (count-atoms '(a (b) c)) --> 3 3. (count-anywhere 'a '(a ((a) b) a)) --> 3 4. (dot-product '(10 20) '(3 4)) --> 10x3 + 20x4 = 110 5. Write a function (flatten '(a (b) () ((c)))) --> (a b c) which removes all levels of parenthesis and returns a flat list of atoms. 6. Write a function (remove-dups '(a 1 1 a b 2 b)) --> (a 1 b 2) which removes all duplicate atoms from a flat list. (Note: there is a built-in remove-duplicates in Common Lisp, do not use it). 

9 . Solutions 1-3 (defun power (a b) "compute a^b - (power 3 2) ==> 9" (if (= b 0) 1 (* a (power a (- b 1))))) (defun count-atoms (exp) "count atoms in expresion - (count-atoms '(a (b) c)) ==> 3" (cond ((null exp) 0) ((atom exp) 1) (t (+ (count-atoms (first exp)) (count-atoms (rest exp)))))) (defun count-anywhere (a exp) "count performances of a in expresion - (count-anywhere 'a '(a ((a) b) (a))) ==> 3" (cond ((null exp) 0) ((atom exp) (if (eq a exp) 1 0)) (t (+ (count-anywhere a (first exp)) (count-anywhere a (rest exp)))))) 

10 . Solutions (defun flatten (exp) "removes all levels of paranthesis and returns flat list of atomsi (flatten '(a (b) () ((c)))) ==> (a b c)" (cond ((null exp) nil) ((atom exp) (list exp)) (t (append (flatten (first exp)) (flatten (rest exp)))))) 

11 . Iteration – adding all elements from a list • Iteration is done by recursion • Analogous to while-loop (defun plus-red (a) (if (null a) 0 (plus (car a) (plus-red (cdr a)) )) ) 

12 . Nested Loops • Example : Cartesian product (defun all-pairs (M N) (if (null M) nil (append (distl (car M) N) (all-pairs (cdr M ) N )) )) (defun distl (x N) (if (null N) nil (cons (list x (car N)) (distl x (cdr N)) )) ) 

13 . Functional arguments and abstraction Suppress details of loop control and recursion example: applying a function to all elements of list (defun mapcar (f x) (if (null x) Another definition of mapcar uses if not cond nil (cons (f (car x)) (mapcar f (cdr x)) )) ) 

14 . Hierarchical structures • Are difficult to handle iteratively example: equal function • eq only handles atoms • initial states – If x and y are both atoms (equal x y) = (eq x y) – If exactly one of x and y is atom (equal x y) = nil (and (atom x) (atom y) (eq x y)) • use car and cdr to write equal recursively 

15 . Equivalency of recursion and iteration • it may be seemed that recursion is more powerful than iteration • in theory these are equivalent • As we said iteration can be done by recursion • by maintaining a stack of activation records we can convert a recursive program to an iterative one. 

16 .Genetic algorithm Common Lisp code 

17 . REDUCE (with 3 arguments) a function to be applied to Final value returned every element of list x a list (defun reduce (f a x) (if (null x) a (f (car x) (reduce f a (cdr x) )) ) ) (reduce #'* '(1 2 3 4 5)) => 120 Here only two values (* 1 (* 2 (* 3 (* 4 5)))) => 120 

18 . Few more examples of using function reduce Examples: (reduce #'* '(1 2 3 4 5)) => 120 (reduce #'append '((1) (2)) :initial-value '(i n i t)) => (I N I T 1 2) ;; list (I N I T) with appended (1) with appended (2) (reduce #'append '((1) (2)) :from-end t :initial-value '(i n i t)) => (1 2 I N I T) (reduce #'- '(1 2 3 4)) == (- (- (- 1 2) 3) 4) => -8 (reduce #'- '(1 2 3 4) :from-end t) ;Alternating sum. == (- 1 (- 2 (- 3 4))) => -2 (reduce #'+ '()) => 0 (reduce #'+ '(3)) => 3 (reduce #'+ '(foo)) => FOO 

19 . Few more examples of using function reduce (reduce #'+ '(foo)) => FOO (reduce #'list '(1 2 3 4)) => (((1 2) 3) 4) ;; assumes to start from beginning of argument list (list (list (list 1 2) 3) 4) (reduce #'list '(1 2 3 4) :from-end t) => (1 (2 (3 4))) (reduce #'list '(1 2 3 4) :initial-value 'foo) => ((((foo 1) 2) 3) 4) (reduce #'list '(1 2 3 4) :from-end t :initial-value 'foo) => (1 (2 (3 (4 foo)))) 

20 . Few more functions reduce reduce uses a binary operation, function, to combine the elements of sequence bounded by start and end. The function must accept as arguments two elements of sequence or the results from combining those  elements. The function must also be able to accept no arguments. If key is supplied, it is used is used to extract the values to reduce. The key function is applied exactly once to each element of sequence in the order implied by the reduction order but not to the value of initial-value, if supplied. The key function typically returns part of the element of sequence. If key is not supplied or is nil, the sequence element itself is used. The reduction is left-associative, unless from-end is true in which case it is right-associative. If initial-value is supplied, it is logically placed before the subsequence (or after it if from-end is true) and included in the reduction operation. In the normal case, the result of reduce is the combined result of function's being applied to successive pairs of elements of sequence. If the subsequence contains exactly one element and no initial-value is given, then that element is returned and function is not called. If the subsequence is empty and an initial- value is given, then the initial-value is returned and function is not called. If the subsequence is empty and no initial-value is given, then the function is called with zero arguments, and reduce returns whatever function does. This is the only case where the function is called with other than two arguments. 

21 .Few more examples of function some • SOME function searches the sequences for values for which predicate returns true. • It there is such list of values that occupy same index in each sequence, return value is true, otherwise false. (some #'alphanumericp "") => NIL (some #'alphanumericp "...") => NIL (some #'alphanumericp "ab...") => T (some #'alphanumericp "abc") => T (some #'< '(1 2 3 4) '(2 3 4 5)) => T (some #'< '(1 2 3 4) '(1 3 4 5)) => T (some #'< '(1 2 3 4) '(1 2 3 4)) => NIL 

22 . Reminder of function let* • let* is similar to let, but the bindings of variables are performed sequentially rather than in parallel. • The expression for the init-form of a var can refer to vars previously bound in the let*. • The form (let* ((var1 init-form-1) (var2 init-form-2) ... (varm init-form-m)) declaration1 declaration2 ... declarationp form1 form2 ... formn) •   first evaluates the expression init-form-1, • then binds the variable var1 to that value; • then it evaluates init-form-2 and binds var2, and so on. • The expressions formj are then evaluated in order; the values of all but the last are discarded (that is, the body of let* is an implicit progn). 

23 . User defined function for crossover random 1.0) generates a random number between 0.0 and 1.0 x and y are chromosomes. This function does “in place” crossover or leaves parents unchanged as they are (defun crossover (x y)    (if (> (random 1.0) 0.6) (list x y)  ;; in this case do nothing, return x and y as in input     ;;else      (let* ((site (random (length x)))  Site is a place of cut (swap (rest (nthcdr site x) )))  Creates child 1     Swap is temporary location       (setf (rest (nthcdr site x)) (rest (nthcdr site y))) Execute crossover       (setf (rest (nthcdr site y)) swap)))) X Y Creates child 2 (nthcdr 2 x) site x swap Child 1 Child 2 swap 

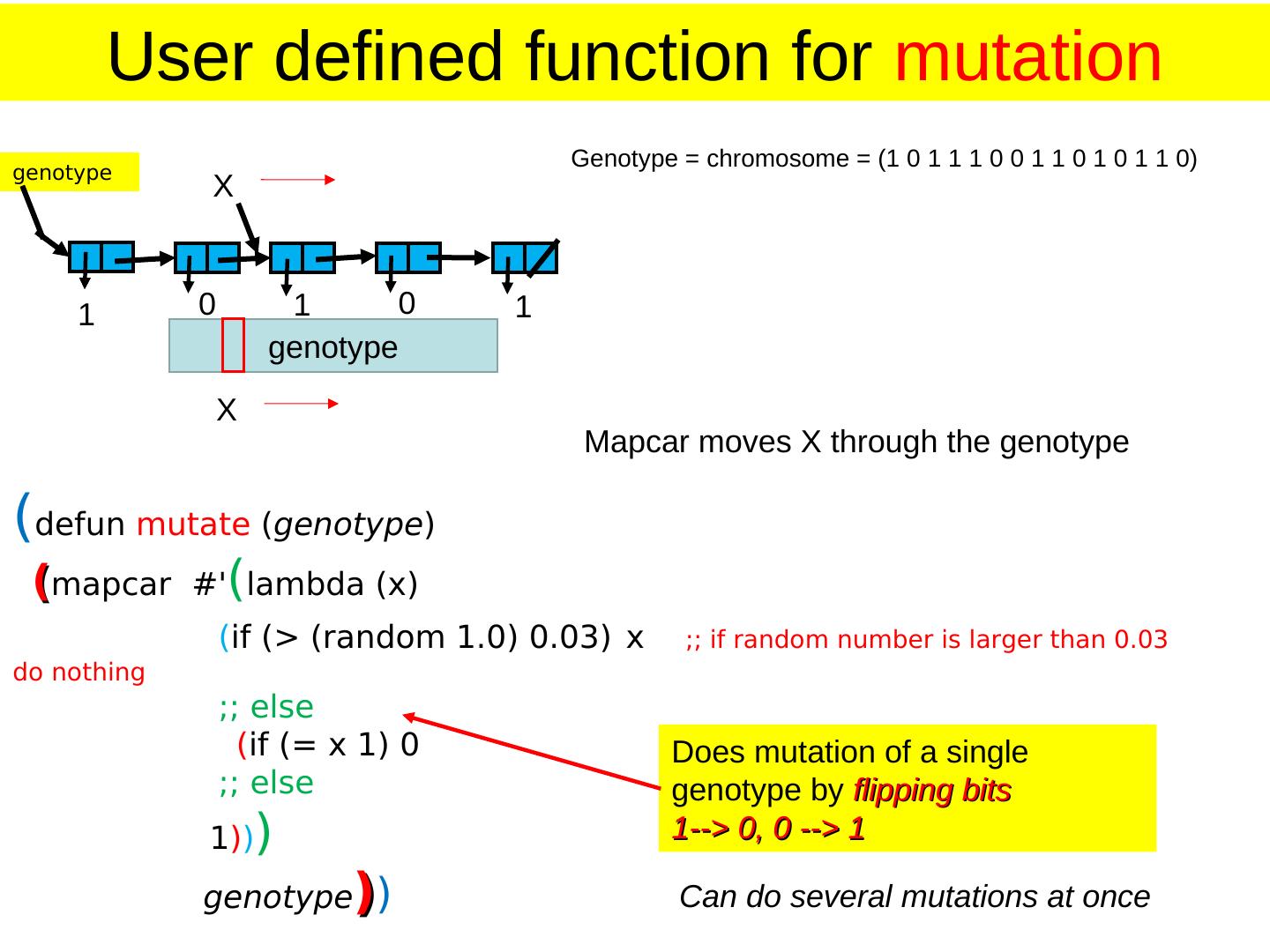
24 . User defined function for mutation Genotype = chromosome = (1 0 1 1 1 0 0 1 1 0 1 0 1 1 0) genotype X 1 0 1 0 1 genotype X Mapcar moves X through the genotype (defun mutate (genotype)     (mapcar #'(lambda (x)          (if (> (random 1.0) 0.03) x ;; if random number is larger than 0.03 do nothing             ;; else             (if (= x 1) 0  Does mutation of a single               ;; else  genotype by flipping bits               1)))  1--> 0, 0 --> 1    genotype)) Can do several mutations at once 

25 . User defined function selectone distributi on 1 …. Genotypen pair cost1 Genotype1 cost3 costn Genotype3 • This function takes distribution and selects one candidate. • It will be used in function reproduce Genotype and distribution are lists of pairs ((cost chromosome) … (cost chromosome)) Selects one parent from population (defun selectone (distribution) distribution   Initializes random   (let ((random (random 1.0))  Initializes prob          (prob 0)          genotype)  Initializes genotype     (some #'(lambda (pair)  •        (incf prob (first pair))  Compares elements of distribution. • • Selects one with higher prob        (if (> random prob) nil  Some selects the first from left that has higher value of prob            ;;else             (setq genotype (rest Apply to the original distribution pair))))         distribution)  Calls function mutate to mutate the      (mutate genotype))) genotype 

26 .Function fitness calculates Calculate fitness function fitness of a chromosome x Function list2num converts list of binary bits s to a number (genotype, object, candidate) x (defun fitness (x)  Calculates fitness of a genotype x   (let ((xarg (/ (list2num x) 1073741823.0))          (v '(0.5 0.25 1.0 0.25))          (c '(0.125 0.375 0.625 0.875))  Set parameters         (w 0.003))      (reduce #'+ (mapcar #'(lambda (vi ci)         (let ((xc (- xarg ci)))           (* vi (exp (* -1 (/ (* 2 w)) xc xc)))))          v c)))) Chromosome is now a • This is of course just one single number xarg particular example of calculating the cost fitness function. • You create your own fitness i=4 -2w ( ( 2 function for your problem. Fitness = vi * e (xarg-ci) REMINDER i=1 (reduce #'* '(1 2 3 4 5)) => 120 

27 . User defined function distribution Takes the initial population and distributes it according to fitness Distributes initial population function Creates genotypes by removing the (defun distribution (population)  duplicates from population   (let* ((genotypes (remove-duplicates population :test #'equal))    (sum (apply #'+ (mapcar #'fitness genotypes))))      Uses function fitness Creates sum of fitness values Calculates fitness of all elements from list genotypes (mapcar #'(lambda (x) (cons (/ (fitness x) sum) x)) genotypes))) Creates a pair of normalized fitness and a genotype x Creates list of pairs for all elements of list genotypes 

28 .Genetic algorithm Common Lisp code (importance of drawing trees for larger functions) reproduce offspring distribution dotimes let length selectone set crossover q nconc I found it very useful to create for myself such trees to know who is calling whom 

29 . Genetic algorithm Common Lisp code: Takes population as argument. This can be some list of random (defun reproduce (population)  binary lists of the same length each.   (let ( (offspring nil)  Initializes offspring to empty list         (d (distribution population) ))  Distributed Distributes initial population     (dotimes (i (/ (length population) 2) )  population Repeats for the length of half population       (let ( (x (selectone d) )  Selects parent x, one from population             (y (selectone d)) Selects parent y, one from population )          (crossover x y)  Does crossover of parents x and y End of adding new         (setq offspring (nconc (list x y) children to list offspring offspring) ) ))      offspring)) Creates new list offspring by adding new children x and y to old list offspring Returns new list offspring