020-Artificial Intelligence programming and Prolog Language Tutorial

1 .Artificial Intelligence programming and Prolog Language Tutorial

2 .Contents What is logic programming? Small Examples The Basics Another Example: Towers of Hanoi Other Examples

3 .What is Logic Programming?

4 .What is Logic Programming? “The use of mathematical logic for computer programming.” (Wikipedia) “A declarative, relational style of programming based on first-order logic.” (Dictionary.com)

5 .History of Prolog Developed in 1972 by Alain Colmerauer and Philippe Roussel Name comes from “PROgramming in LOGic” A solution to the debate about which kinds of logic to use

6 .History of Logic Programming Came about in 1960s and 1970s due to debates about using declarative or procedural representations in AI Stanford and Edinburgh – declarative MIT - procedural Developed Planner in 1969 (first language in the proceduralistic paradigm).

7 .Systems for Logic Programming ALF CLP ECLiPSe Elf Fish Flang Gödel KLIC LIFE MONA Oz System RELFUN SAMPLE XSB Just to name a few….

8 .Systems for Logic Programming, cont. Prolog is the most common system Prolog has many variations: &-Prolog, And-parallel Prolog. ACE, And-Or-parallel Prolog. Actor Prolog Andorra-I, an Or- and (deterministic) and-parallel Prolog. Aurora, Or-parallel Prolog. cu-Prolog, a constraint logic programming language lambda Prolog LeanTaP , a small theorem prover written in SICStus Prolog. Logtalk , an extension for Object-Oriented Programming in Prolog. Mixtus , an automatic partial evaluator for full Prolog. Muse, Or-parallel Prolog.

9 .Prolog Structure

10 .Prolog Structure Prolog facts – a database of predicates and associations. Prolog rules – define new predicates by using Prolog facts. Note: Prolog considers capital letters to denote variables , not predicates.

11 .Prolog Structure – Queries A query searches the database for the first fact that satisfies its goal. If a fact is found then it either unifies the variable with a constant or Prolog returns yes . If a fact is not found that meets that condition then Prolog returns no .

12 .Prolog Structure – disjunction and conjunction . Use a semi-colon to request subsequent answers. In other words, a semi-colon signifies disjunction .  A comma signifies conjunction . 

13 .How Prolog Works: Example 1 Example of data base: instructor ( perkowski , ee271) instructor ( perkowski , ee171) instructor ( perkowski , ee478) enrolled ( alan - cheng , ee475) enrolled ( matthew , ee171) enrolled (alan-cheng,ee171) enrolled (alan-cheng,ee271) enrolled (chris-clark,ee271) enrolled ( edison-tsai , ee171) enrolled ( chris - clark , ee171) This is the database of Prolog facts.

14 .How Prolog Works, cont. Prolog rules: teaches (P,S) :- instructor (P,C), enrolled (S,C) This is to say that an instructor only teaches if he teaches a class and students are enrolled in that class. teaches (Professor, Student) :- instructor (Professor, Class), enrolled ( Student,Class ) teaches (Professor, Student)  instructor (Professor, Class), enrolled ( Student,Class ) instructor (Professor, Class), enrolled ( Student,Class )  teaches (Professor, Student)

15 .How Prolog Works, cont. Prolog answers queries based off of the database that has been given. ?enrolled ( chris - clark , ee271) yes ?enrolled (X, ee271) alan-cheng chris - clark ?teaches (X, alan-cheng ) perkowski ?teaches (X, chris - clark ) Perkowski Jeske greenwood

16 .Expanding Database in Prolog Imagine what happens if we expand the database: instructor ( perkowski , ee271) instructor ( perkowski , ee171) instructor ( perkowski , ee478) enrolled ( jeske , ee171) enrolled (greenwood, ee171) enrolled (alan-chen,ee171) enrolled (alan-chen,ee271) enrolled (chris-clark,ee271) enrolled ( edison-tsai , ee171) enrolled ( chris - clark , ee171) instructor ( bebis , cs365) instructor ( looney , cs311) instructor ( yuksel , cs446) instructor ( helfand , cs493) instructor ( quint , math486) enrolled ( ben , cs365) enrolled (bill, cs365) enrolled (bill, cs446) enrolled ( brian , cs311) enrolled ( brian , cs365) enrolled ( brittney , cs311) enrolled ( brittney , cs365) enrolled ( brittney , cs446) enrolled ( cody , cs311) enrolled ( cody , cs365) enrolled ( danielle , cs365) enrolled ( danielle , cs446) enrolled ( danielle , cs493) enrolled ( david , cs365) enrolled ( javier , cs365) enrolled ( jeffrey , cs365) enrolled ( jessica , cs311) enrolled ( jessica , cs446) enrolled ( jessica , math486) enrolled ( joel , cs365) enrolled ( joseph , cs311) enrolled ( joseph , cs365) enrolled ( joseph , cs446) enrolled ( joseph , cs493) enrolled ( joseph , math486) enrolled ( kellen , cs365) enrolled ( matts , cs311) enrolled ( matts , cs365) enrolled ( mattw , cs311) enrolled ( mattw , cs365) enrolled ( mattw , cs446) enrolled ( miran , cs365) enrolled ( ryan , cs365) enrolled ( samuel , cs365) enrolled ( shane , cs311) enrolled ( shane , cs365) enrolled ( shane , cs446) enrolled (tiffany, cs311) enrolled (tiffany, cs365) enrolled (tiffany, cs446)

17 .How Prolog Works, asking questions to data base ?enrolled (X, cs365) ben bill brian brittney cody danielle david javier jeffrey joel joseph kellen matts mattw miran ryan samuel shane tiffany This list now gives us the entire roster of students in CS 365.

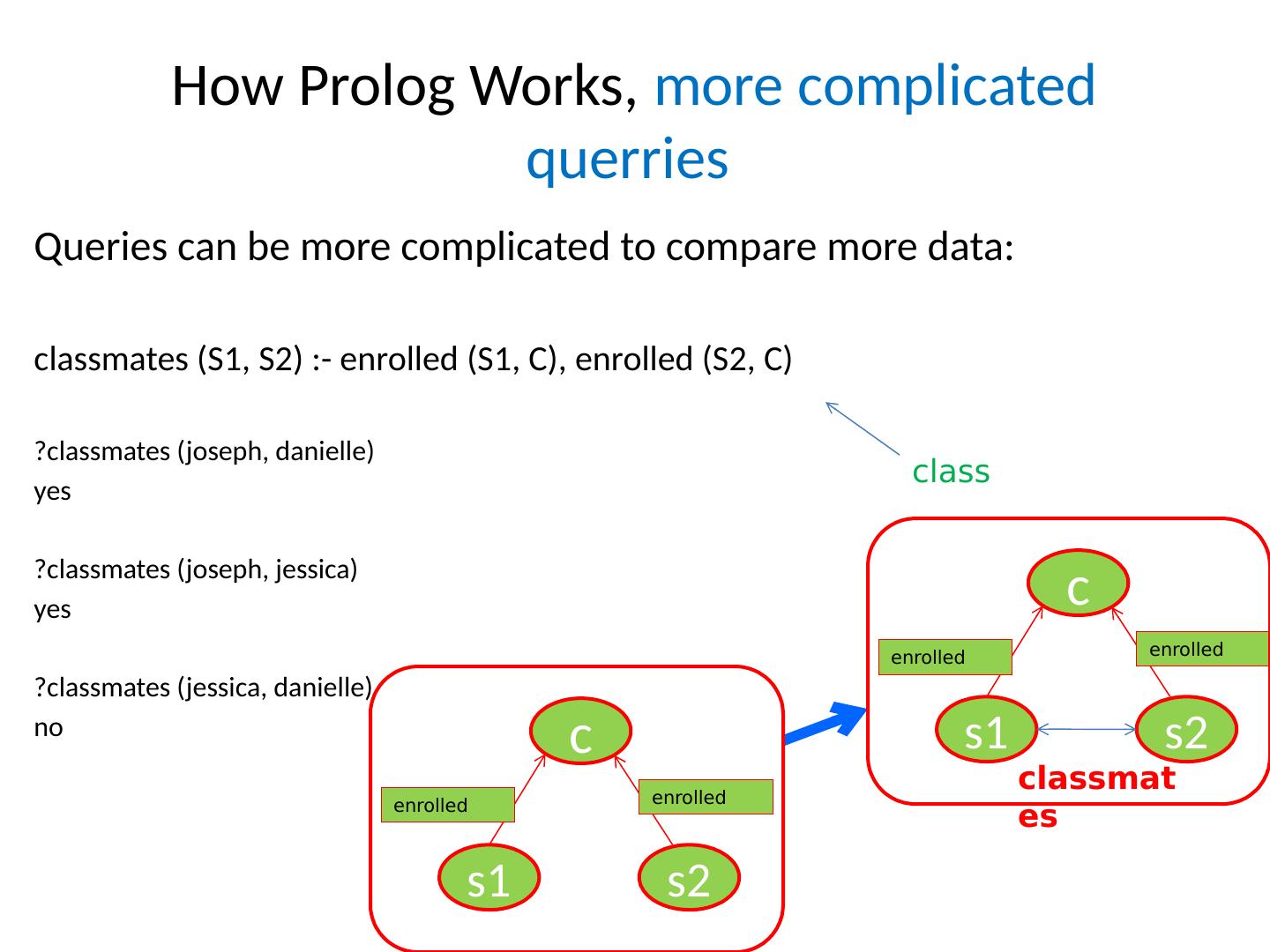
18 .How Prolog Works, more complicated querries Queries can be more complicated to compare more data: classmates (S1, S2) :- enrolled (S1, C), enrolled (S2, C) ?classmates ( joseph , danielle ) yes ?classmates ( joseph , jessica ) yes ?classmates ( jessica , danielle ) no class c s2 s1 enrolled enrolled c s2 s1 enrolled enrolled classmates

19 .How Prolog Works, more complicated querries classmates (S1, S2, C) :- enrolled (S1, C), enrolled (S2, C) ?classmates (joseph, danielle, C) cs365 cs446 cs493 no ?classmates (joseph, jessica, C) math ?classmates (jessica, danielle, C) no

20 .Family Data base

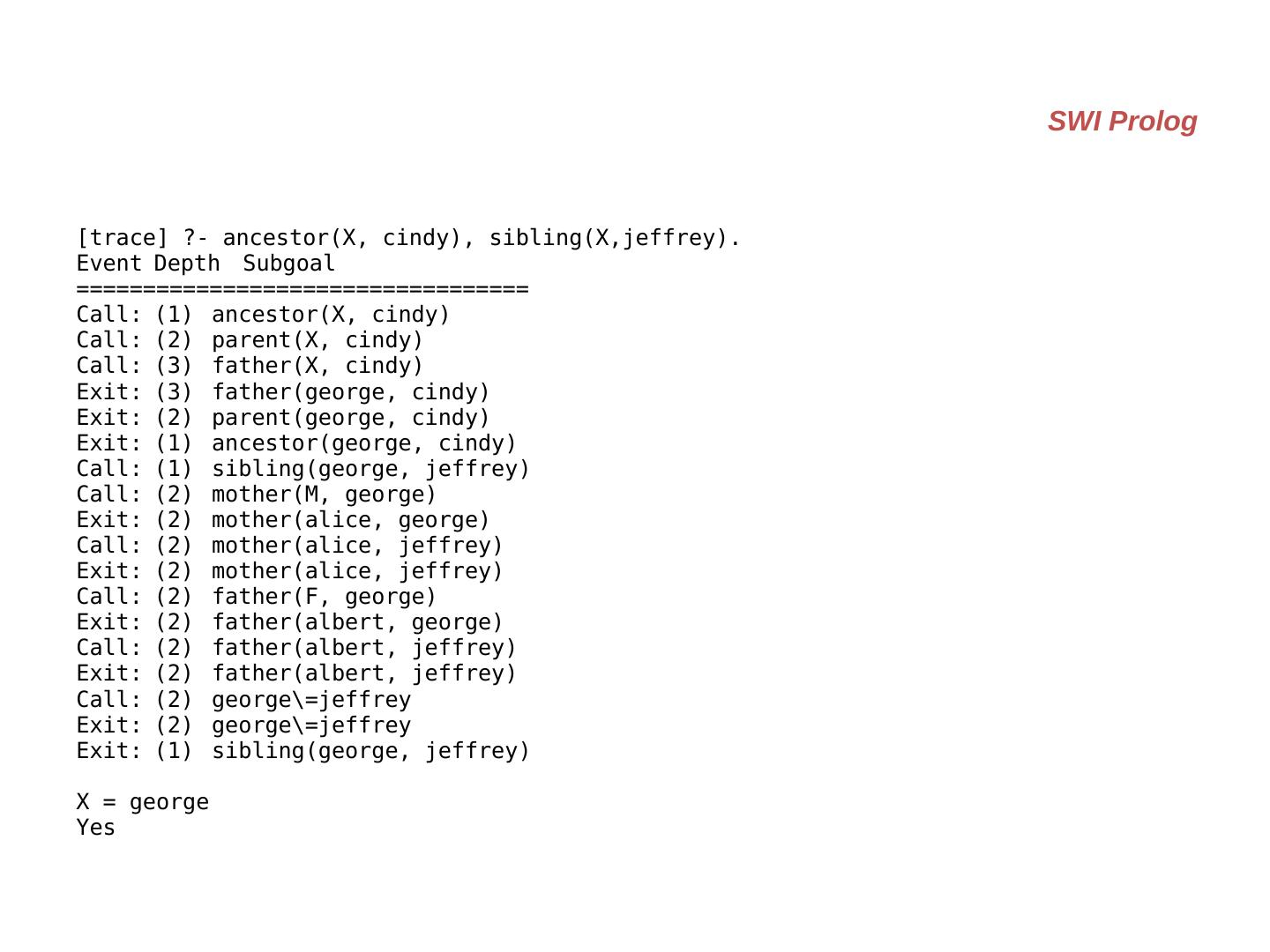
21 .parent (X,Y) :- father (X,Y). parent (X,Y) :- mother (X,Y). grandparent (X,Z) :- parent (X,Y), parent (Y,Z). ancestor (X,Z) :- parent (X,Z). ancestor (X,Y) :- parent (X,Y), ancestor (Y,Z). sibling (X,Y) :- mother (M,X), mother (M,Y), father (F,X), father (F,Y), X \= Y. cousin (X,Y) :- parent (U,X), parent (V,Y), sibling (U,V). father (albert, jeffrey). mother (alice, jeffrey). father (albert, george). mother (alice, george). father (john, mary). mother (sue, mary). father (george, cindy). mother (mary, cindy). father (george, victor). mother (mary, victor).

22 .?- [kinship]. % kinship compiled 0.00 sec, 3,016 bytes Yes ?- ancestor(X, cindy), sibling(X, jeffrey). X = george  Yes ?- grandparent(albert, victor). Yes ?- cousin(alice, john). No ?- sibling(A,B). A = jeffrey, B = george ;  A = george, B = jeffrey ;  A = cindy, B = victor ;  A = victor, B = cindy ;  No SWI Prolog

23 .Unification

24 .Prolog Structure - Unification A query resolves by unifying all of its elements. A constant unifies with itself and any variable. Scope is limited to the rule in which a variable occurs. When a variable is unified with a constant in a rule, all instances of that variable in that rule are unified to that constant.

25 .Process of making one predicate same as another . A query resolves by unifying all of its elements . A constant unifies with itself and any variable. Scope is limited to the rule in which a variable occurs. When a variable is unified with a constant in a rule, all instances of that variable in that rule are unified to that constant. PROLOG STRUCTURE - UNIFICATION

26 .Example of Unification

27 .Prolog Structure - Backtracking In more complex examples, Prolog uses backtracking to find possible solutions . Prolog will attempt to resolve the first fact of its rule , unifying any variables with the first constant that satisfies that fact It then attempts to resolve the rest of that rules facts . If it is unable to do so under those conditions it “backs up” and tries again with the next available unifying constant.

28 .Clauses Programs are constructed from A number of clauses : <head> :- <body> Clauses have three forms: hypotheses (facts) conditions (rules) goals Both <head > and <body> are composed of relationships (also called predications or literals ) assertions (database) questions

29 .Relationships Represent properties of and relations among the individuals A relationship is application of a predicate to one or more terms Terms: atoms (or constants): john, 25, … variables (begin with uppercase letters ): X, … compounds Horn clause form : At most one relationship in <head>