037-Robot Motion Planning

1 . Robot Motion Planning CSE398/498-011 23 Jan 05 Supporting References • “Motion Planning Using Potential Fields,” R. Beard & T. McClain, BYU, 2003 • You should download this from the course page and read it 1 

2 . Let’s Assume… • We have an a priori map of the environment OR • We have sufficient sensor information to reconstruct the environment The Basic Motion Planning Problem • Given an initial robot position and orientation in a potentially cluttered workspace C, how should the robot move in order to reach an objective pose? 2 

3 . Class Objectives • Examine alternate approaches to motion planning • Roadmap Approach: – Visibility Graph Methods • Cell Decomposition: – Exact Decomposition – Approximate: Uniform discretization & quadtree approaches • Potential Fields 1. The Visibility Graph Method GOAL START 1) Model obstacles as polygons 3 

4 .The Visibility Graph Method (cont’d) GOAL START 2) Construct a graph G(V,E). All polygon vertices are added to V, as are the start and goal positions. The Visibility Graph Method (cont’d) GOAL START 3) All vertices that are visible to one another are connected with an edge. These edges are added to E. 4 

5 .The Visibility Graph Method (cont’d) GOAL START 4) Polygon edges are also added to E. Then we only need to find the shortest path from the start vertex to the goal vertex in G. How can we find this??? The Visibility Graph Method (cont’d) GOAL START Path We can find the shortest path using Dijkstra’s Algorithm!!! 5 

6 . 2. Exact Cell Decomposition Method GOAL 2 6 10 12 7 1 4 9 13 3 11 5 8 START 1) Decompose Region Into Cells Exact Cell Decomposition Method (cont’d) GOAL 2 6 10 12 7 1 4 9 13 3 11 5 8 START 2) Construct Adjacency Graph 6 

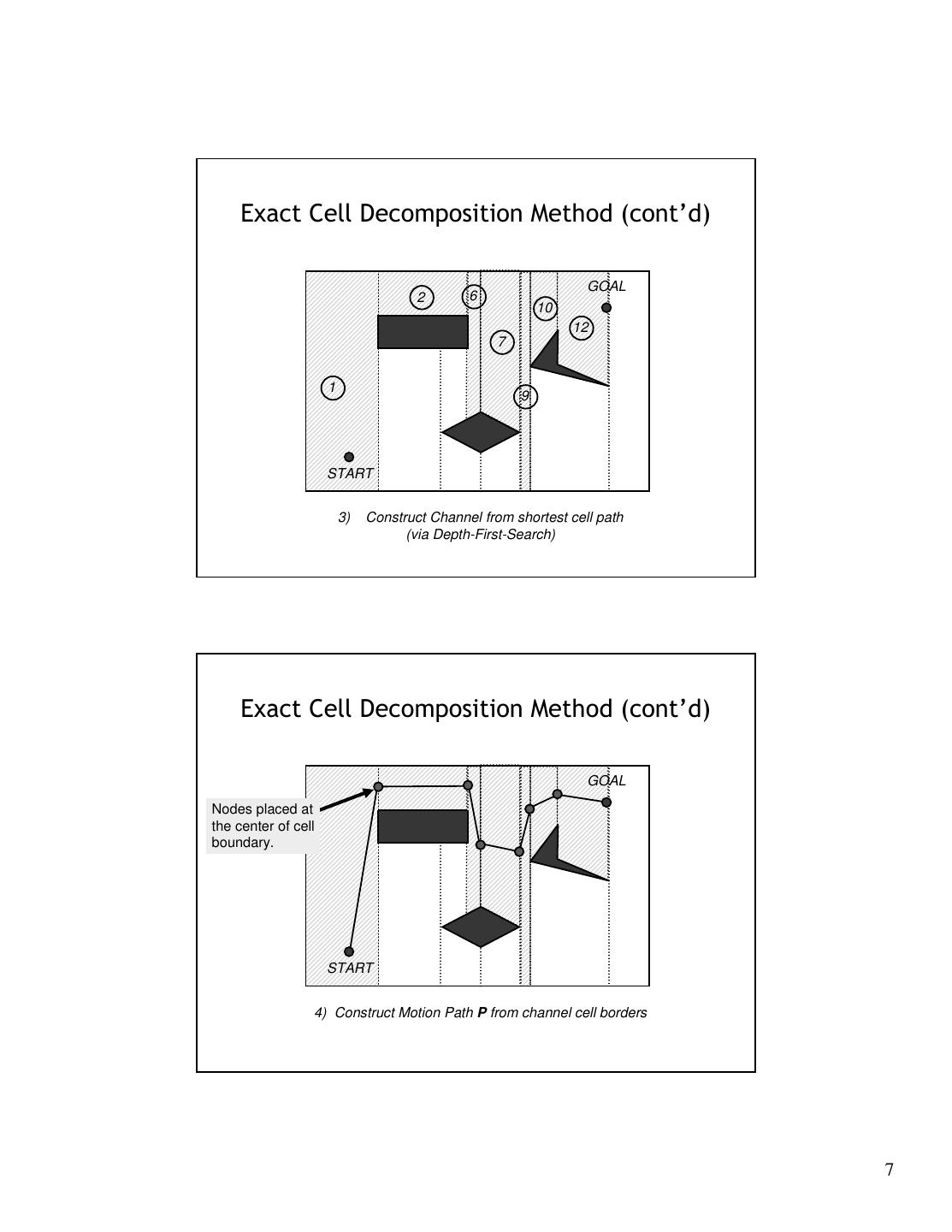
7 . Exact Cell Decomposition Method (cont’d) GOAL 2 6 10 12 7 1 9 START 3) Construct Channel from shortest cell path (via Depth-First-Search) Exact Cell Decomposition Method (cont’d) GOAL Nodes placed at the center of cell boundary. START 4) Construct Motion Path P from channel cell borders 7 

8 .2b. Exact Cell Decomposition Method Using Euclidean Metric GOAL START Exact Cell Decomposition Method Using Euclidean Metric GOAL START 8 

9 . 3. Approximate Cell Decomposition 1. Perform cell tessellation of configuration space C – Uniform or quadtree 2. Generate the cell graph G(V,E) – Each cell v ∈ C free ⊆ C corresponds to a vertex in V – Two vertices vi,vj ∈ V are connected by an edge eij if they are adjacent (8-connected for exact) – Edges are weighted by Euclidean distance 3. Find the shortest path from vinit to vgoal Step 1: Cell Decomposition Uniform Quadtree 9 

10 . Cell Decomposition Issues 1. Continuity of trajectory a function of resolution 2. Computational complexity increases dramatically with resolution 3. Inexactness. Is this cell an obstacle or in Cfree? Neighbors r Cell Decomposition Simulations No Obstacles Single Obstacle 10 

11 . Cell Decomposition Simulations Multiple Obstacles No Path Approximate Cell Summary • PROS – Applicable to general obstacle geometries – Provides shorter paths than exact decomposition • CONS – Performance a function of discretization resolution (δ) • Inefficiencies • Lost paths • Undetected collisions – Number of graph vertices |V| grows with δ2 and Dijkstra’s runs in O(|E| lg |V|) (an A* implementation in O(V2)) 11 

12 . The Potential Field Approach Some Background • Introduced by Khatib [1986] initially as a real-time collision avoidance module, and later extended to motion planning • Robot motion is influenced by an artificial potential field – a force field if you will – induced by the goal and obstacles in the robot’s configuration space C (all of the possible positions of the robot) • The field is modeled by a potential function E(x,y) over C 12 

13 . Some Background (cont’d) • Motion policy control law is akin to gradient descent on the potential function • A shortcoming of the approach is the lack of performance guarantees: the robot can become trapped in local minima • Koditschek’s extension introduced the concept of a “navigation function” - a local-minima free potential function Example Application: Target Tracking with Obstacle Avoidance 13 

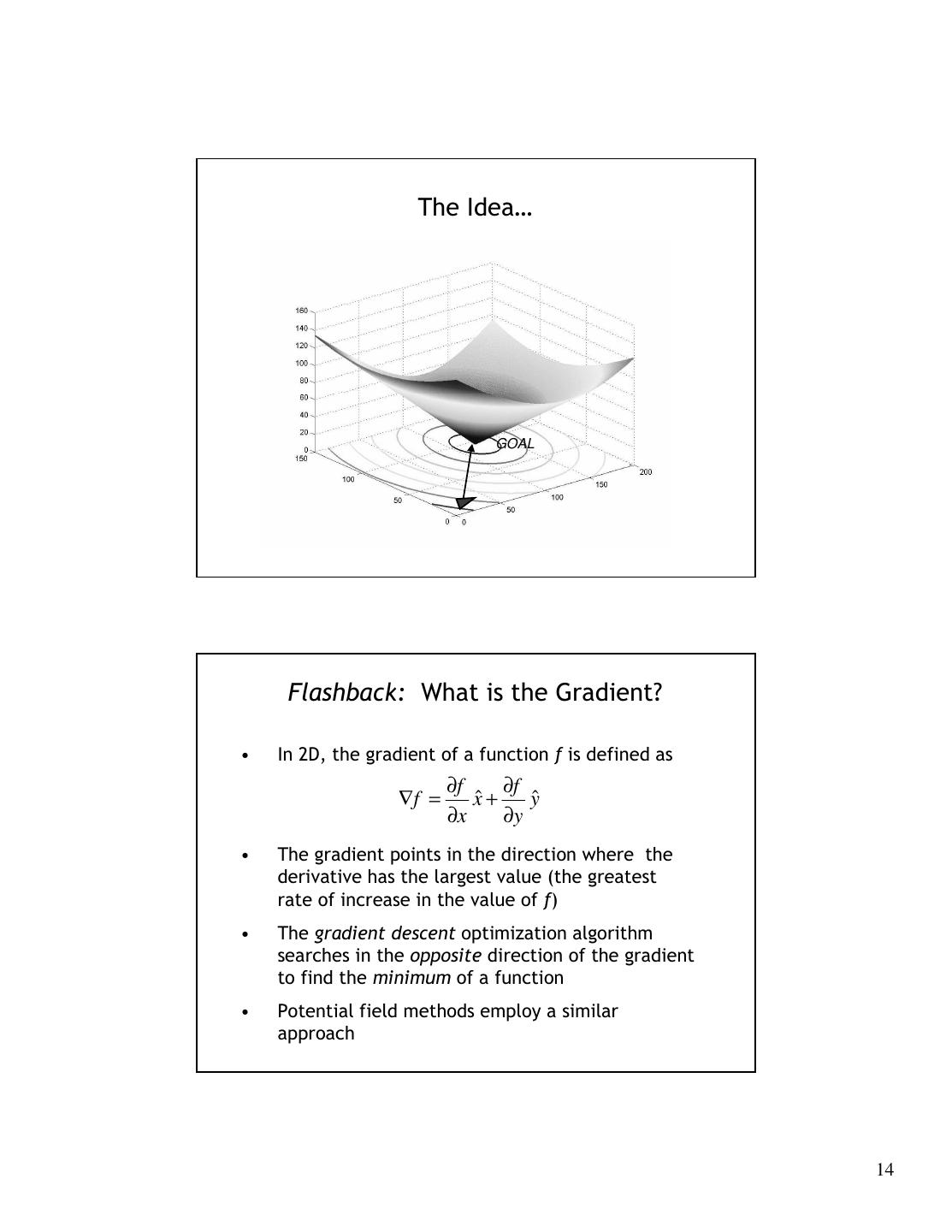
14 . The Idea… GOAL Flashback: What is the Gradient? • In 2D, the gradient of a function f is defined as ∂f ∂f ∇f = xˆ + yˆ ∂x ∂y • The gradient points in the direction where the derivative has the largest value (the greatest rate of increase in the value of f) • The gradient descent optimization algorithm searches in the opposite direction of the gradient to find the minimum of a function • Potential field methods employ a similar approach 14 

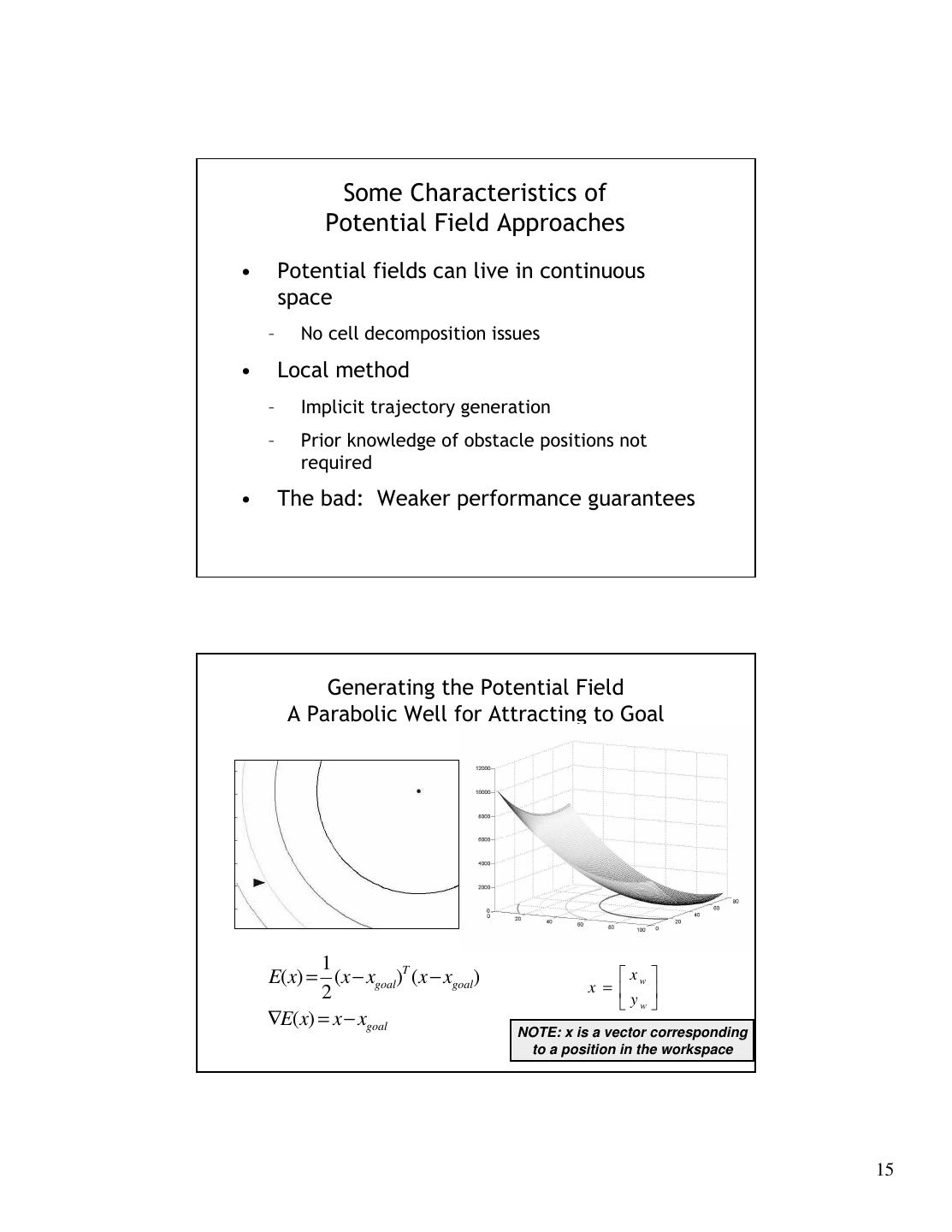
15 . Some Characteristics of Potential Field Approaches • Potential fields can live in continuous space – No cell decomposition issues • Local method – Implicit trajectory generation – Prior knowledge of obstacle positions not required • The bad: Weaker performance guarantees Generating the Potential Field A Parabolic Well for Attracting to Goal 1 E(x) = (x − xgoal)T (x − xgoal) x  x =  w 2  yw  ∇E(x) = x − xgoal NOTE: x is a vector corresponding to a position in the workspace 15 

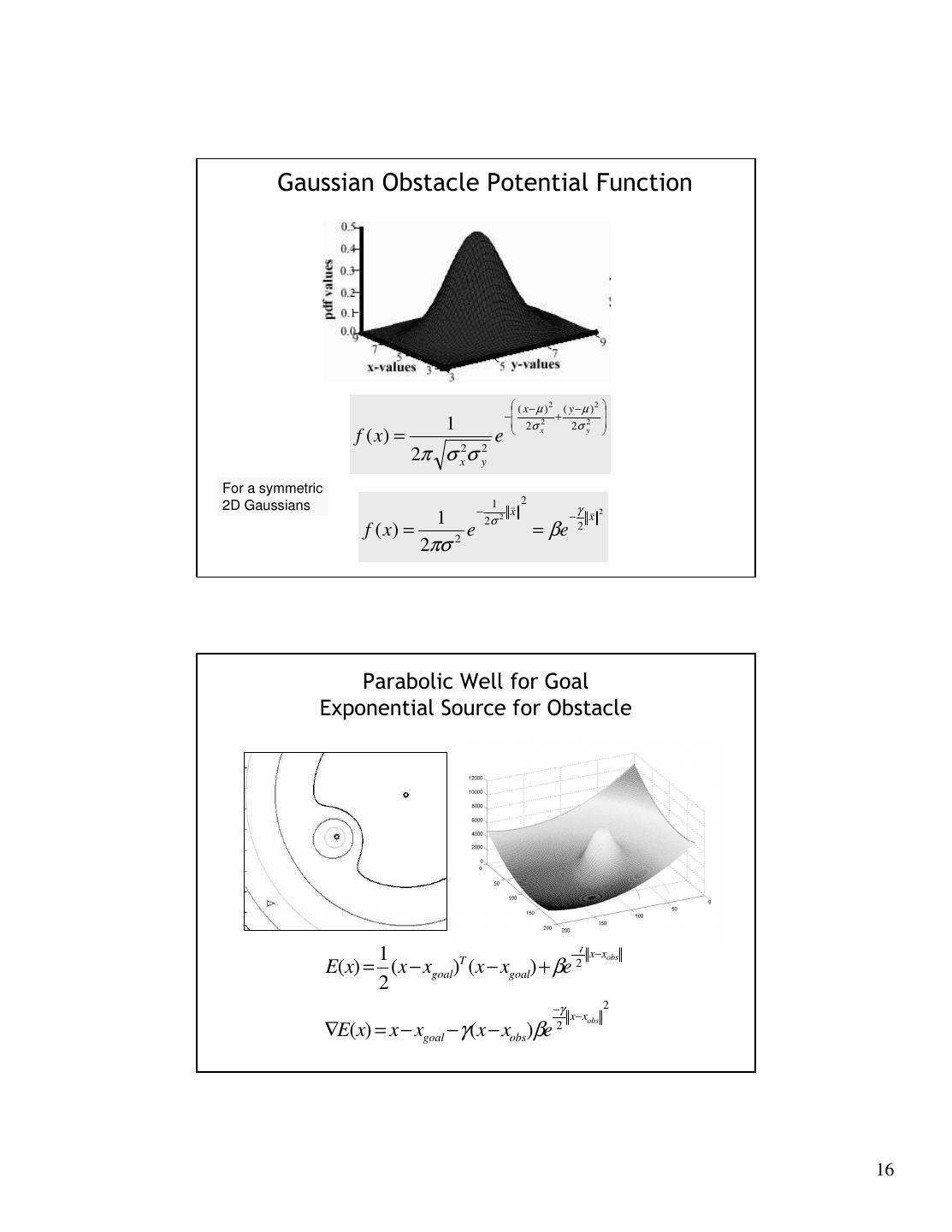
16 . Gaussian Obstacle Potential Function  ( x − µ )2 ( y − µ )2  − +  1  2σ 2 2σ y2  f ( x) = e  x  2π σ x2σ y2 For a symmetric 2D Gaussians 1 v 2 − x γ v 2 1 2σ 2 − x f ( x) = e = βe 2 2πσ 2 Parabolic Well for Goal Exponential Source for Obstacle −γ 2 1 x−xobs E(x) = (x − xgoal)T (x − xgoal) + βe 2 2 −γ 2 x−xobs ∇E(x) = x − xgoal − γ (x − xobs)βe 2 16 

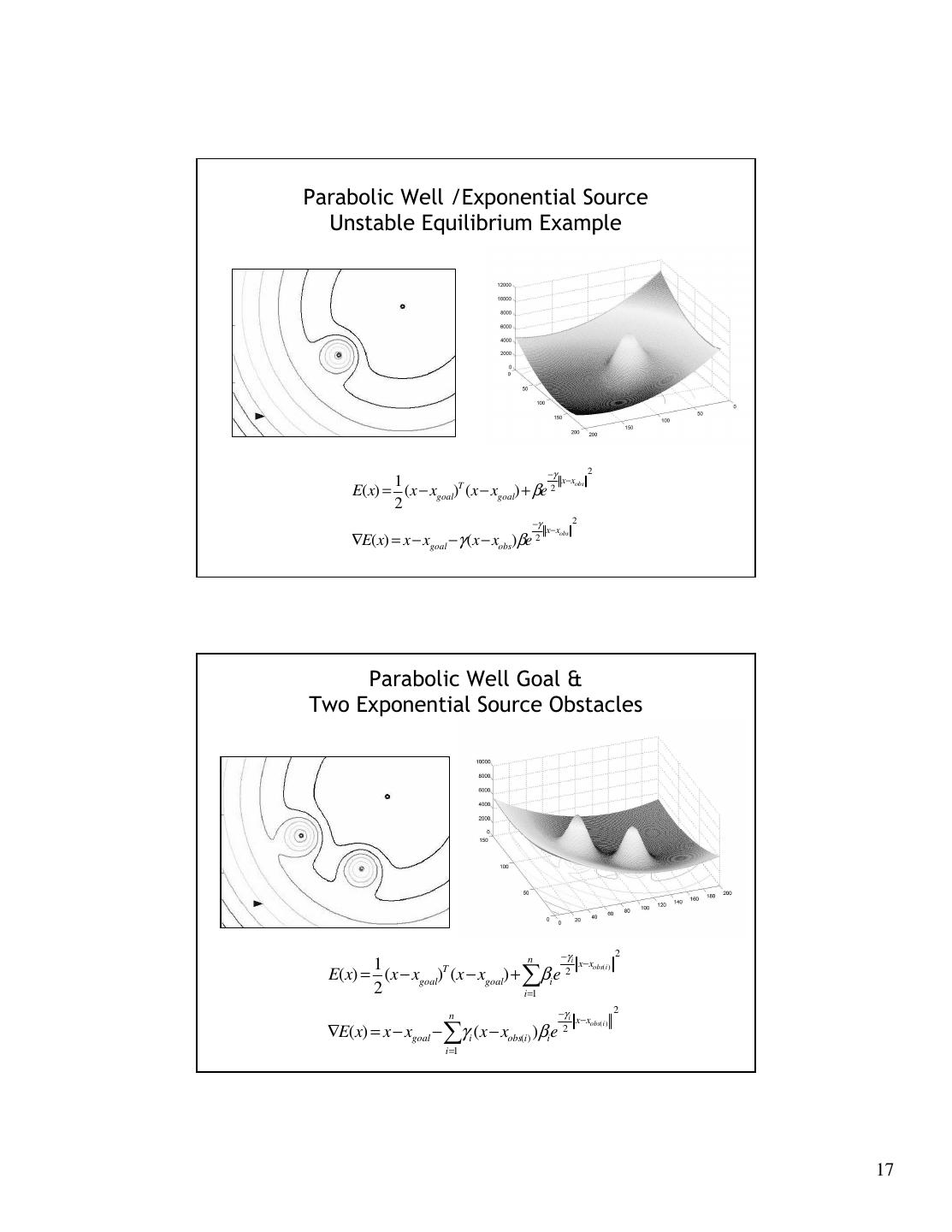
17 .Parabolic Well /Exponential Source Unstable Equilibrium Example −γ 2 1 x−xobs E(x) = (x − xgoal)T (x − xgoal) + βe 2 2 −γ 2 x−xobs ∇E(x) = x − xgoal − γ (x − xobs)βe 2 Parabolic Well Goal & Two Exponential Source Obstacles n −γ 2 1 i x− xobs( i ) E(x) = (x − xgoal)T (x − xgoal) + ∑βie 2 2 i =1 n −γ i 2 x−xobs( i ) ∇E(x) = x − xgoal − ∑γ i (x − xobs(i) )βie 2 i =1 17 

18 . Parabolic Well Goal & Two Exponential Source Obstacles n −γ 2 1 i x− xobs( i ) E(x) = (x − xgoal)T (x − xgoal) + ∑βie 2 2 i =1 n −γ i 2 x−xobs( i ) ∇E(x) = x − xgoal − ∑γ i (x − xobs(i) )βie 2 i =1 Parabolic Well Goal & Two Exponential Source Obstacles Local Minima n −γ 2 1 i x− xobs( i ) E(x) = (x − xgoal)T (x − xgoal) + ∑βie 2 2 i =1 n −γ i 2 x−xobs( i ) ∇E(x) = x − xgoal − ∑γ i (x − xobs(i) )βie 2 i =1 18 

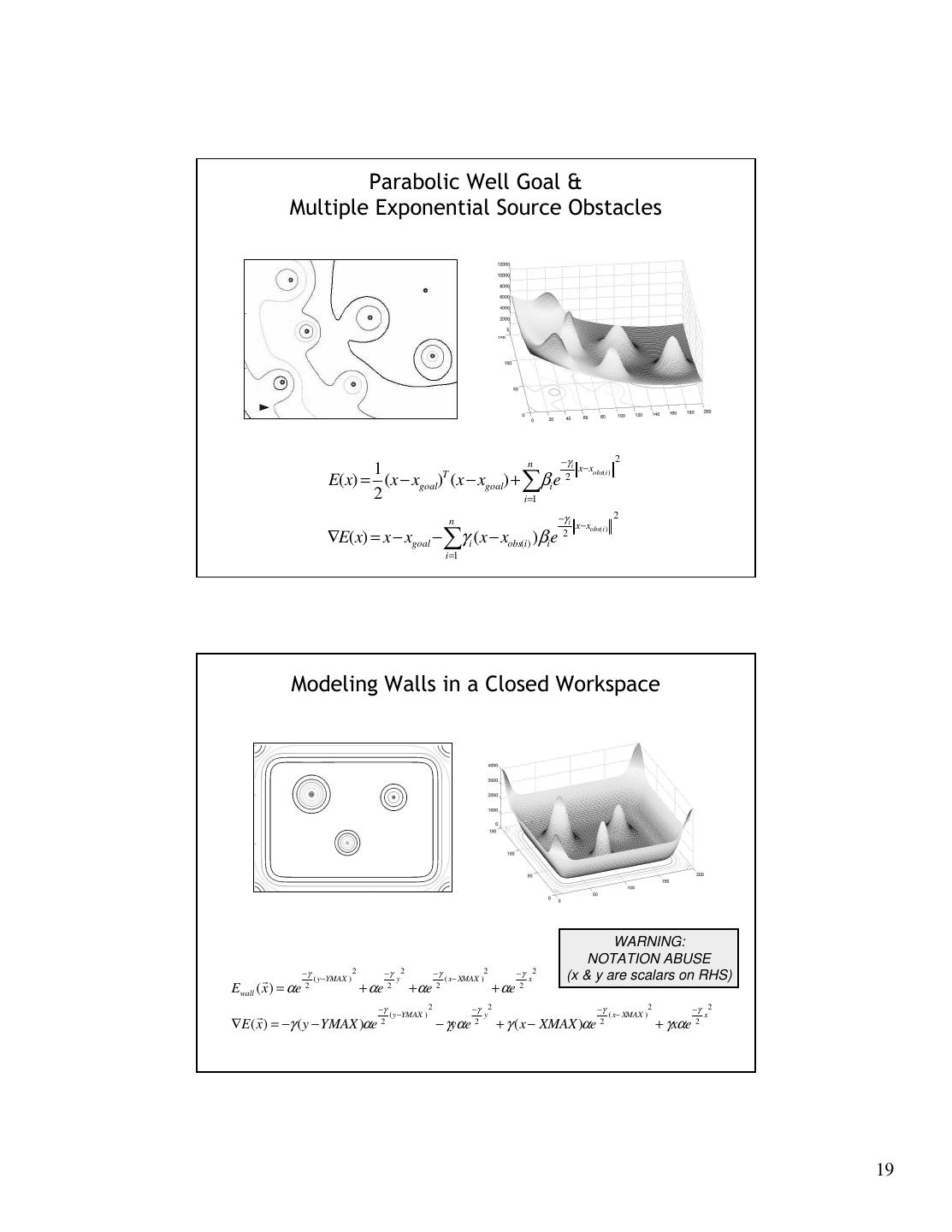
19 . Parabolic Well Goal & Multiple Exponential Source Obstacles n −γ 2 1 i x− xobs( i ) E(x) = (x − xgoal)T (x − xgoal) + ∑βie 2 2 i =1 n −γ i 2 x−xobs( i ) ∇E(x) = x − xgoal − ∑γ i (x − xobs(i) )βie 2 i =1 Modeling Walls in a Closed Workspace WARNING: NOTATION ABUSE −γ 2 −γ 2 −γ 2 −γ 2 (x & y are scalars on RHS) r ( y −YMAX ) y ( x− XMAX ) x Ewall ( x ) = αe 2 + αe 2 + αe 2 + αe 2 −γ 2 −γ 2 −γ −γ2 2 r ( y −YMAX ) y ( x− XMAX ) x ∇E ( x ) = −γ ( y − YMAX )αe 2 − γyαe 2 + γ ( x − XMAX )αe 2 + γxαe 2 19 

20 . A Summary Example Issues with Reactive Approaches Presented • Obstacles are not points – Model as points – Bound with ellipses (one or more obstacles) • Local minima proliferate with multiple obstacles, and failure to achieve goal often results in global motion planning task – Combine with global/discrete approaches • Best first search • Wavefront propagation • Voronoi 20 

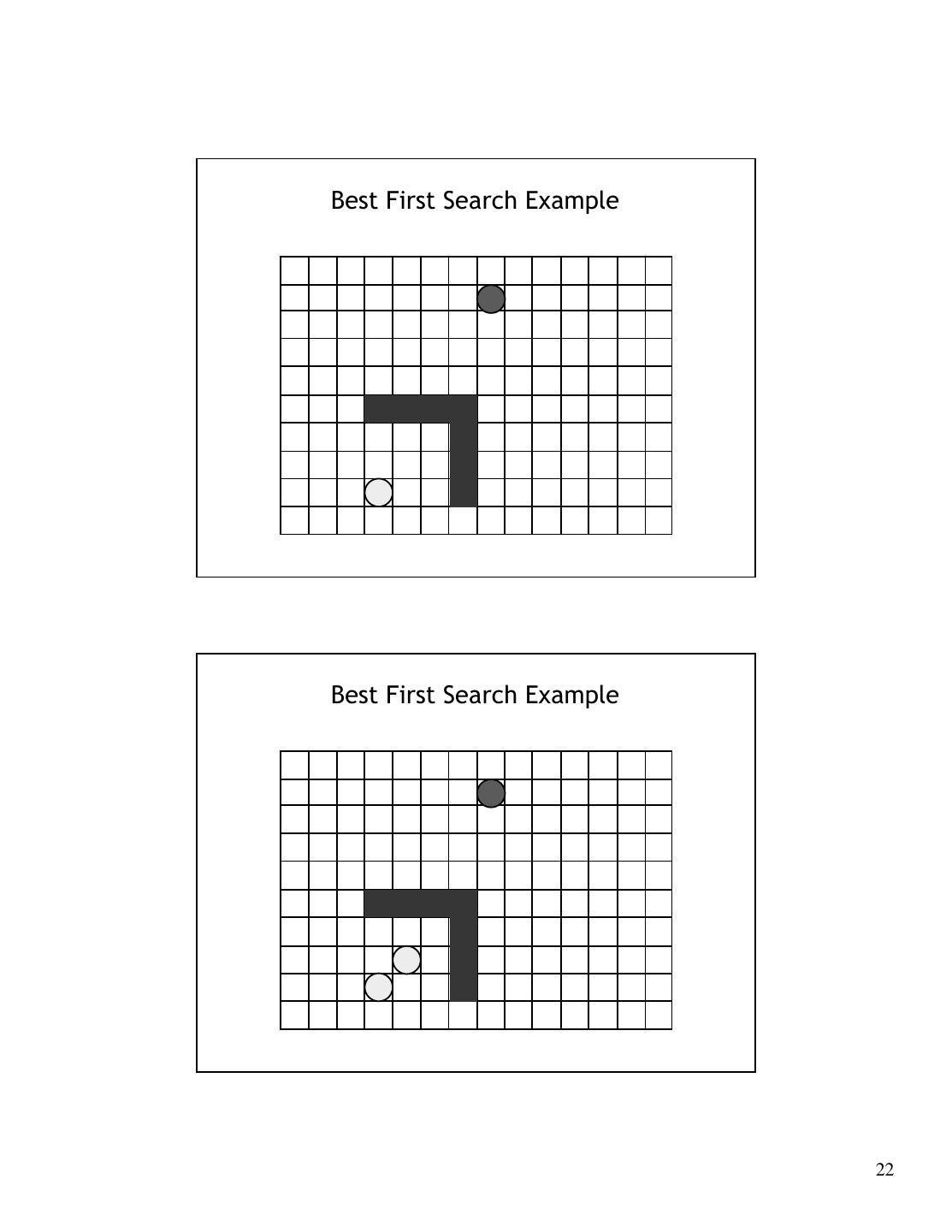
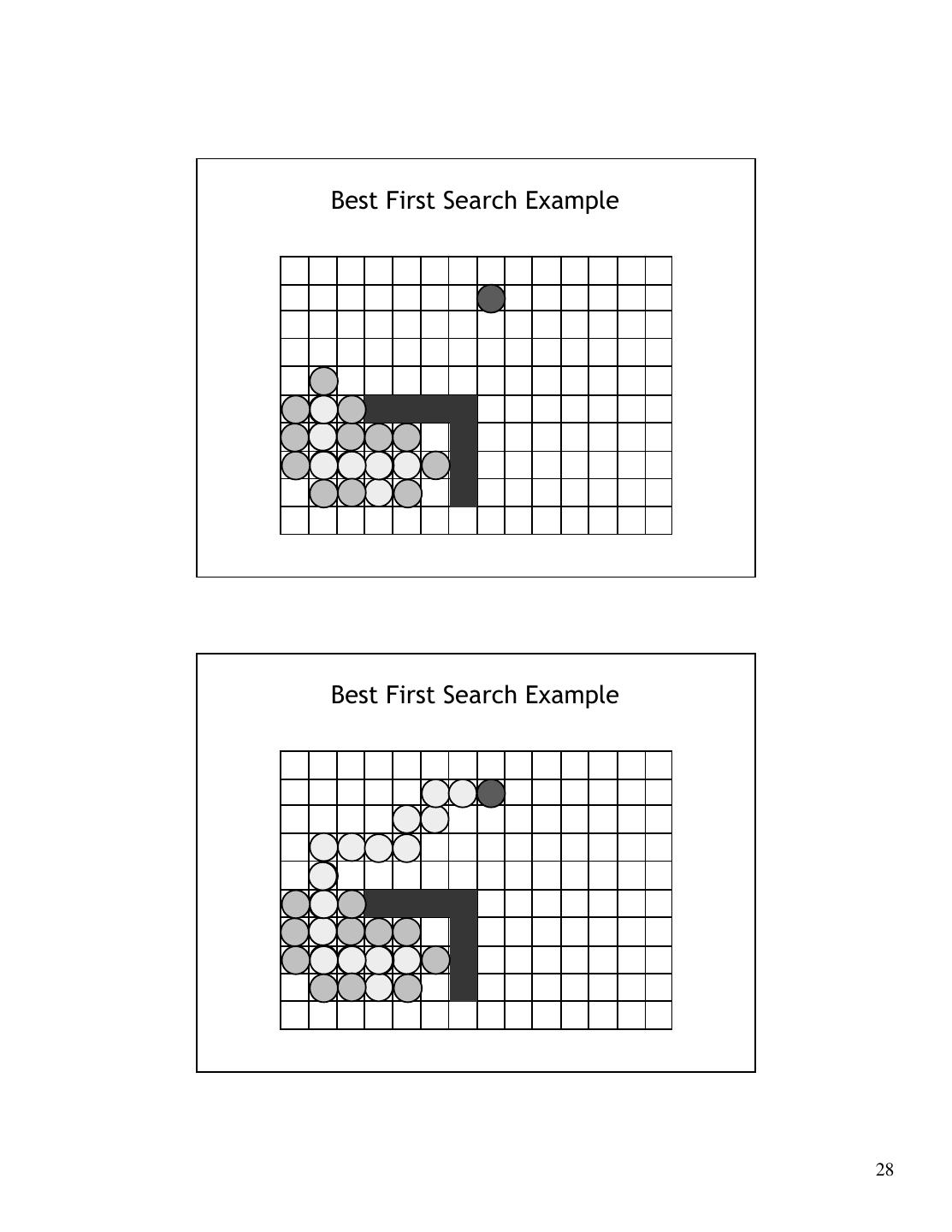
21 . Summary • We examined 2 different approaches to motion planning • In our application, C is fixed BUT Cfree changes over time • Often, only local sensing information is available so it may not be necessary to calculate a complete path to the goal • Potential fields are computationally inexpensive, as you only need to compute the potential local to the robot Best First Search 1. Workspace discretized into cells 2. Insert (xinit,yinit) into list OPEN 3. Find all 4-way neighbors to (xinit,yinit) that have not been previously visited and insert into OPEN 4. Sort neighbors by minimum potential 5. Form paths from neighbors to (xinit,yinit) 6. Delete (xinit,yinit) from OPEN 7. (xinit,yinit) = minPotential(OPEN) 8. GOTO 2 until (xinit,yinit)=goal (SUCCESS) or OPEN empty (FAILURE) 21 

22 .Best First Search Example Best First Search Example 22 

23 .Best First Search Example Best First Search Example 23 

24 .Best First Search Example Best First Search Example 24 

25 .Best First Search Example Best First Search Example 25 

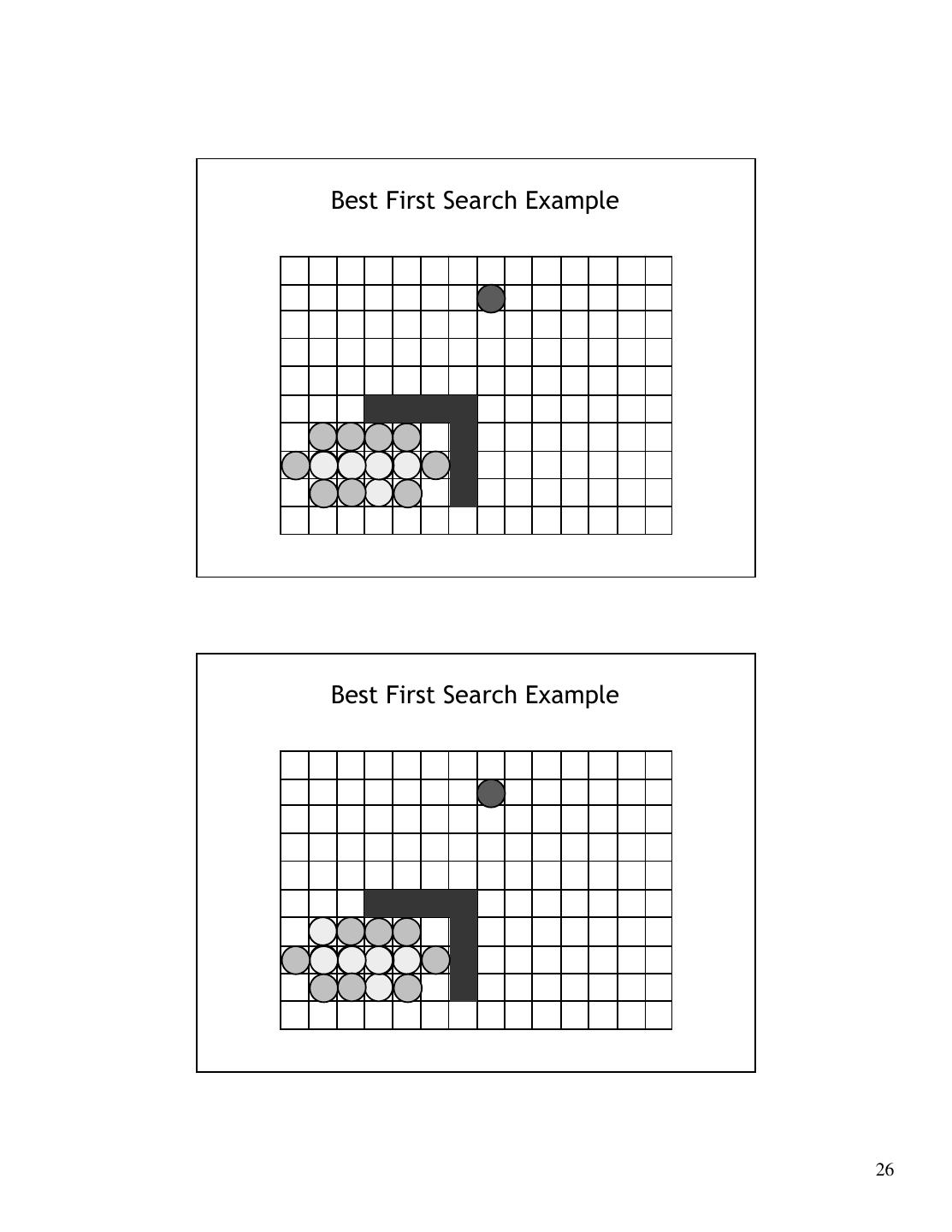
26 .Best First Search Example Best First Search Example 26 

27 .Best First Search Example Best First Search Example 27 

28 .Best First Search Example Best First Search Example 28