- 快召唤伙伴们来围观吧
- 微博 QQ QQ空间 贴吧
- 文档嵌入链接
- 复制
- 微信扫一扫分享
- 已成功复制到剪贴板
SVM原理与应用
展开查看详情
1 .SVM 原理与应用 HITSCIR-TM Group zkli - 李泽魁
2 .大纲 背景 线性分类 非线性分类 松弛变量 多元 分类 应用 工具包 2
3 .大纲 背景 线性分类 非线性分类 松弛变量 多元 分类 应用 工具包 3
4 .SVM 背景 支持向量 机 support vector machine SVM 4
5 .为什么要用 SVM( 个人观点 ) 分类效果好 上手快 N 种语言的 N 个 Toolkit 理论基础完备 妇孺皆知的好模型 找工作需要它 ( 利益相关 :面试狗一只 ) 应用与原理 5
6 .SVM 发展历史 重要理论 基础 1 60 年代, Vapnik 和 Chervonenkis 提出 VC 维理论 重要理论基础 2 1982 年, Vapnik 提出 结构风险最小化 理论 支持 向量机 (Support Vector Machine) 是 Cortes 和 Vapnik 于 1995 年首先提出 的 它在解决 小样本 、 非线性 及 高维模式识别 中表现出许多特有的优势,并能够推广应用到函数拟合等其他机器学习问题 中 6
7 .作者之一简介 Vapnik 《Statistical Learning Theory 》 作者 书中详细的论证了 统计机器学习 之所以区别于传统机器学习的本质,就在于统计机器学习能够精确的给出学习效果,能够解答需要的样本数等等一系列问题。 7
8 .SVM 理论 基础 1 (比较八股) 统计 学习理论 的 VC 维 理论 (Statistical Learning Theory 或 SLT ) 是 研究有限样本情况下机器学习规律的 理论 ( Vapnik-Chervonenkis Dimension) 反映 了函数集的学习能力, VC 维 越大则学习机器越 复杂 8
9 .SVM 理论 基础 2 (比较八股) 结构风险最小化 机器学习本质 上就是 一种对问题真实模型的 逼近。这个与问题真实解之间的误差,就叫做 风险 。 结构化风险 = 经验风险 + 置信风险 经验风险 = 分类器在给定样本上的误差 置信风险 = 分类器在未知文本上分类的结果的 误差,代表 了我们在多大程度上可以信任分类器在未知文本上分类的结果。(无法准确估值,给出估计的区间) 9
10 .SVM 理论 基础 2 (比较八股) 结构化风险 = 经验风险 + 置信风险 置信风险因素: 样本数量,给定的样本数量越大,学习结果越有可能正确,此时置信风险越小; 分类函数的 VC 维,显然 VC 维越大,推广能力越差,置信风险会变大。 泛化误差界的 公式* R(w)≤ R emp (w)+ Ф( n/h) 公式中 R(w) 就是真实风险, Remp (w) 就是经验风险, Ф(n/h) 就是置信风险 。 统计学习的目标从经验风险最小化变为了寻求经验风险与置信风险的和最小,即结构风险最小。 10
11 .SVM 理论 基础(小结) 统计学习理论的 VC 维 理论 SVM 关注的是 VC 维 结构风险最小化 R(w )≤ R emp (w)+ Ф( n/h) 11
12 .SVM 特性 小 样本 与问题的复杂度比起来, SVM 算法要求的样本数是相对比较少的 非线性 SVM 擅长应付样本数据线性不可分的情况,主要通过 松弛变量和 核函数技术来实现 高维 模式识别 例如文本的向量 表示,几万维,反例 : KNN 12
13 .大纲 背景 线性分类 非线性分类 松弛变量 多元 分类 应用 工具包 13
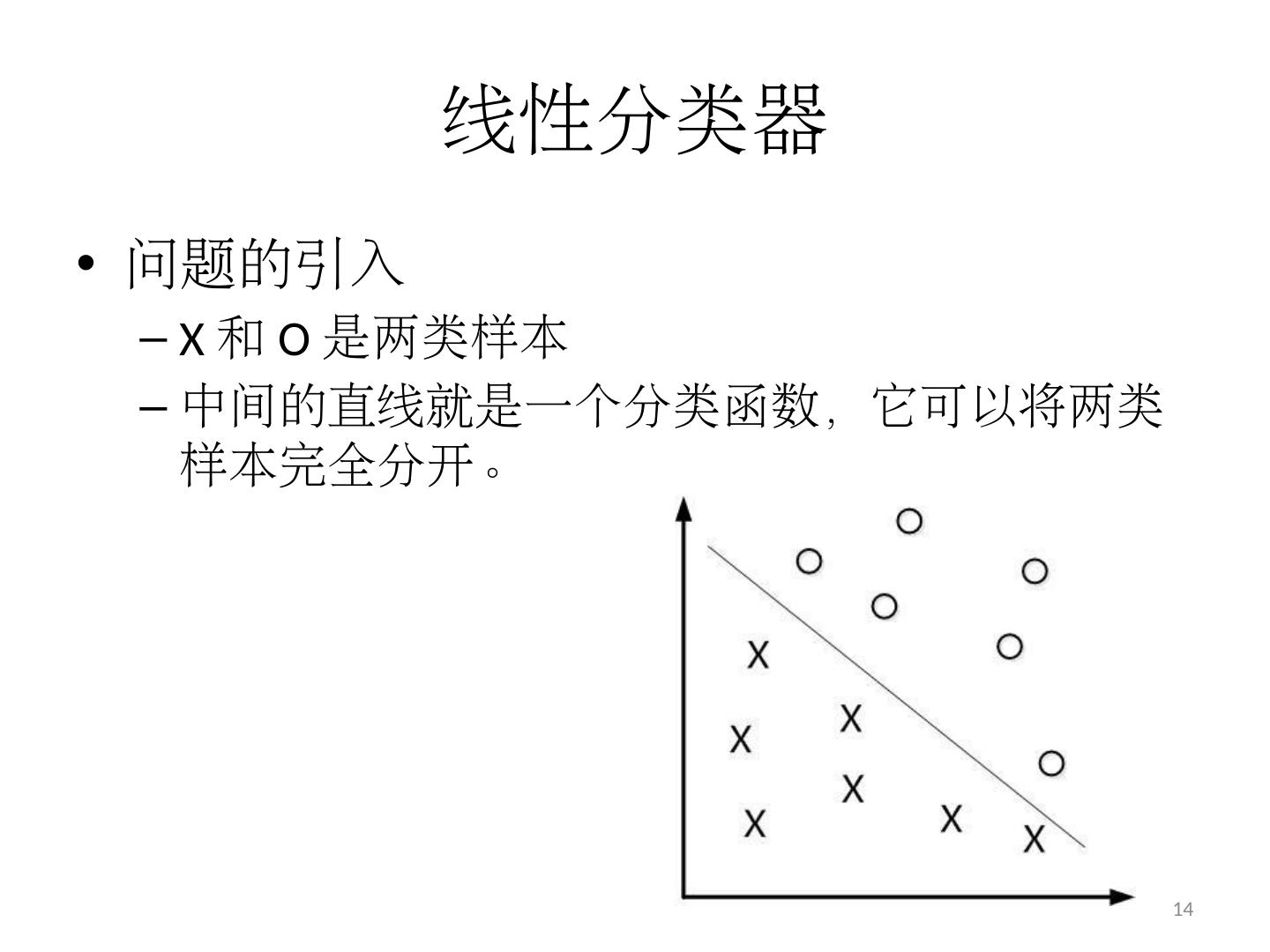
14 .线性分类器 问题的引入 X 和 O 是两类样本 中间的直线就是一个分类函数,它可以将两类样本完全分开。 14
15 .线性 函数? 在一维空间里就是一个 点 在二维空间里就是一条 直线 在 三维空间 里就是一个 平面 …… 如果不关注空间的维数,这种线性函数还有一个统一的名称 —— 超平面 (Hyper Plane) 15
16 .线性 函数 分类问题 例如我们有一个线性 函数 g(x)= wx+b 我们可以取阈值为 0 ,这样当有一个样本 x i 需要判别的时候,我们就看 g(x i ) 的值 。 若 g(x i )>0 ,就判别为 类别 O 若 g(x i )<0 ,则判别为 类别 X Tips w 、 x 、 b 均可以是向量 中间那条直线的表达式是 g(x)=0 ,即 wx+b =0 ,我们也把这个函数叫做分类 面 16
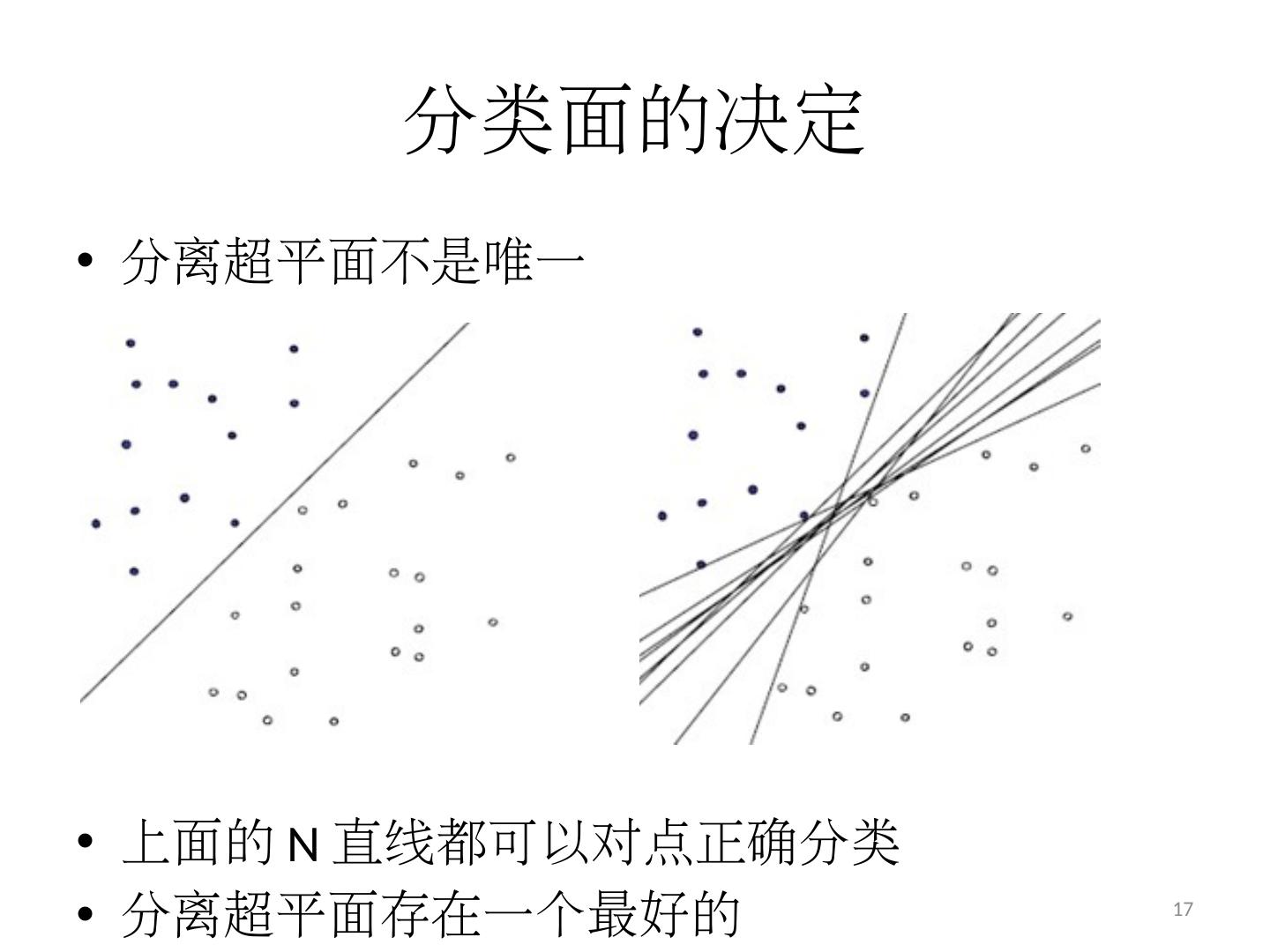
17 .分类面的决定 分离超平面不是 唯一 上面 的 N 直线 都可以对点正确 分类 分离超平面存在一个最好 的 17
18 .分类 面的“好坏”量化 一个很直观的感受是, 让“离直线最近的点,距离直线尽可能地远” 就是 分割的间隙越大越好,把两个类别的点分得 越开越好 18
19 .“分类间隔”的引入 文本分类分类时样本格式 label ( 标示出这个样本属于哪个类别 ) feature (文本 特征所组成的向量 ) 假设 label=±1 ,我们就可以 定义 一个样本点到某个超平面的 间隔为 ( 这是定义 ) δ i = y i ( wx i +b ) 19 ^
20 .分类间隔 δ i = y i ( wx i +b ) y i ( wx i +b ) 总大于 0 的,而且它的 值等于 | wx i +b | 如果某个样本属于该类别 的话, wx i +b >0 , 而 y i 也大于 0 反之, wx i +b <0 ,而 y i 也小于 0 现在把 w 和 b 进行一下归一化,即用 w/||w|| 和 b/||w|| 分别代替原来的 w 和 b ,那么间隔就可以写 成 20 ^
21 .分类 间隔 几何间隔 解析几何中点 x i 到直线 g(x)=0 的距离 公式 推广一下,是到超平面 g(x)=0 的距离, g(x)=0 就是上节中提到的分类 超平面 ||w|| 是什么符号? ||w|| 叫做向量 w 的 范数, 向量 长度 其实指的是它的 2- 范数 用归一化的 w 和 b 代替原值之后的间隔有一个专门的名称,叫做 几何间隔 21
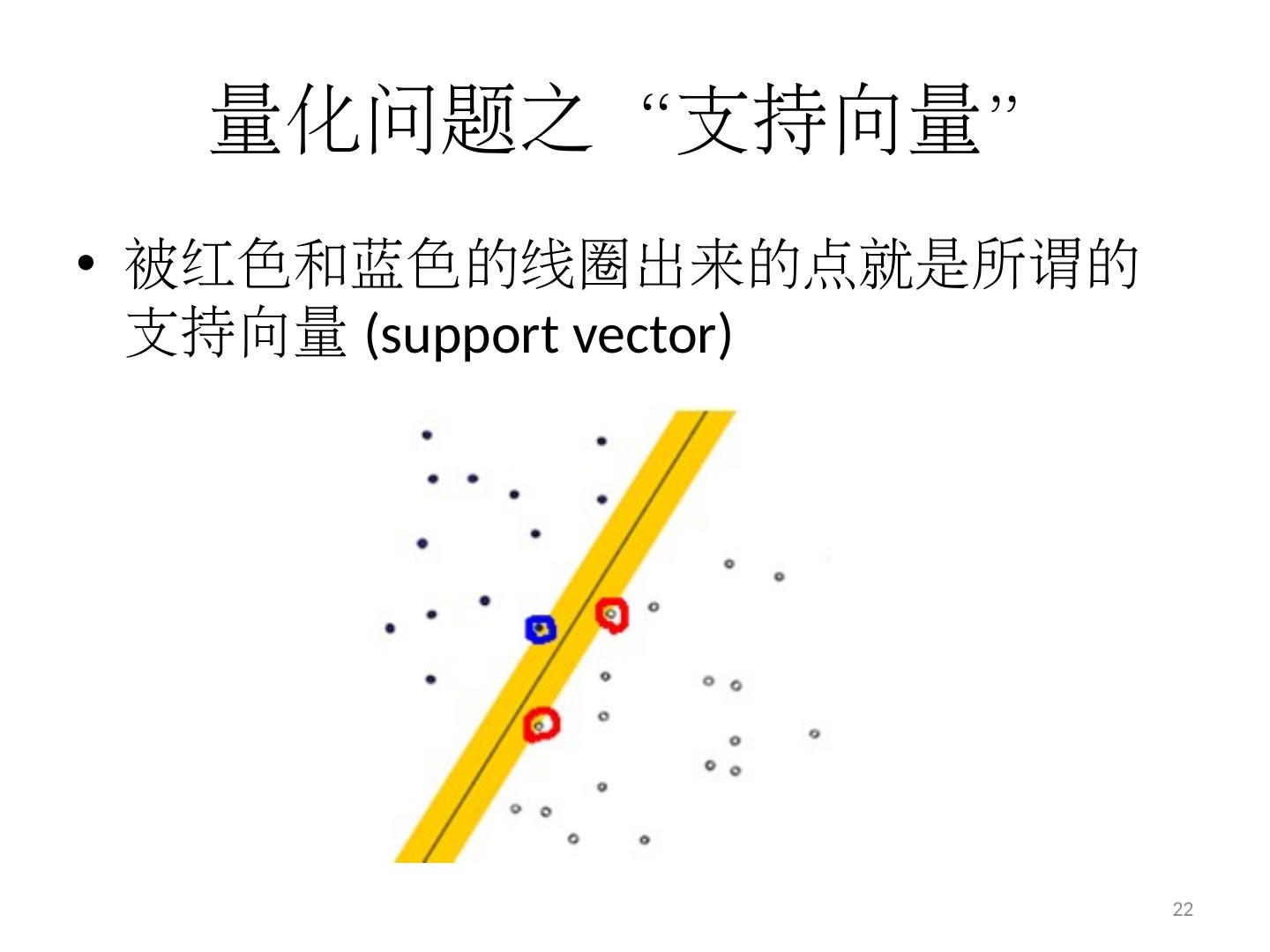
22 .量化问题之“支持向量” 被红色和蓝色的线圈出来的点就是所谓的支持向量 (support vector ) 22
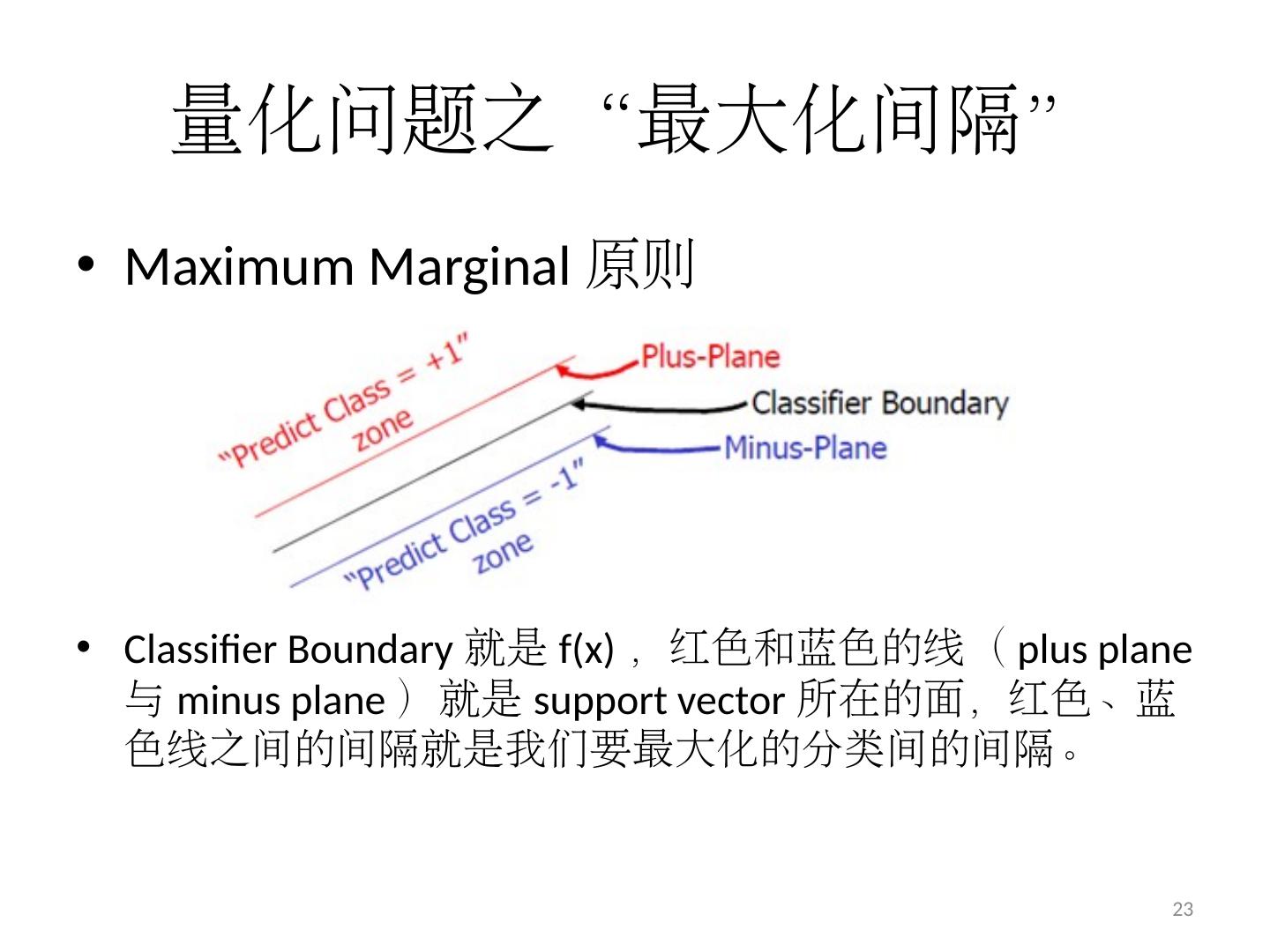
23 .量化问题之“最大化间隔” Maximum Marginal 原则 Classifier Boundary 就是 f(x) ,红色和蓝色的线( plus plane 与 minus plane )就是 support vector 所在的面,红色、蓝色线之间 的 间隔 就是 我们要最大化的分类间 的间隔。 23
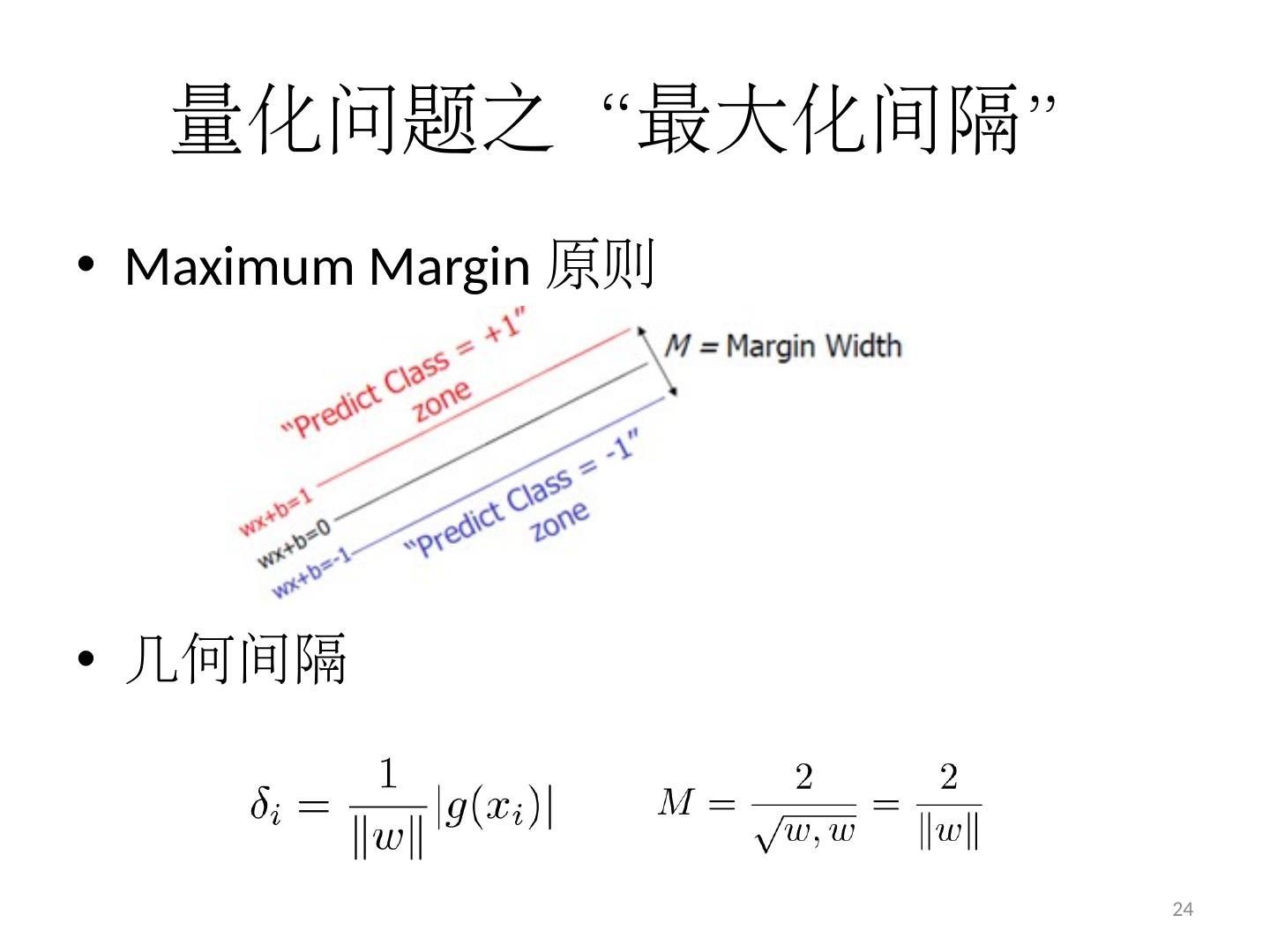
24 .量化问题之“最大化间隔” Maximum Margin 原则 几何间隔 24
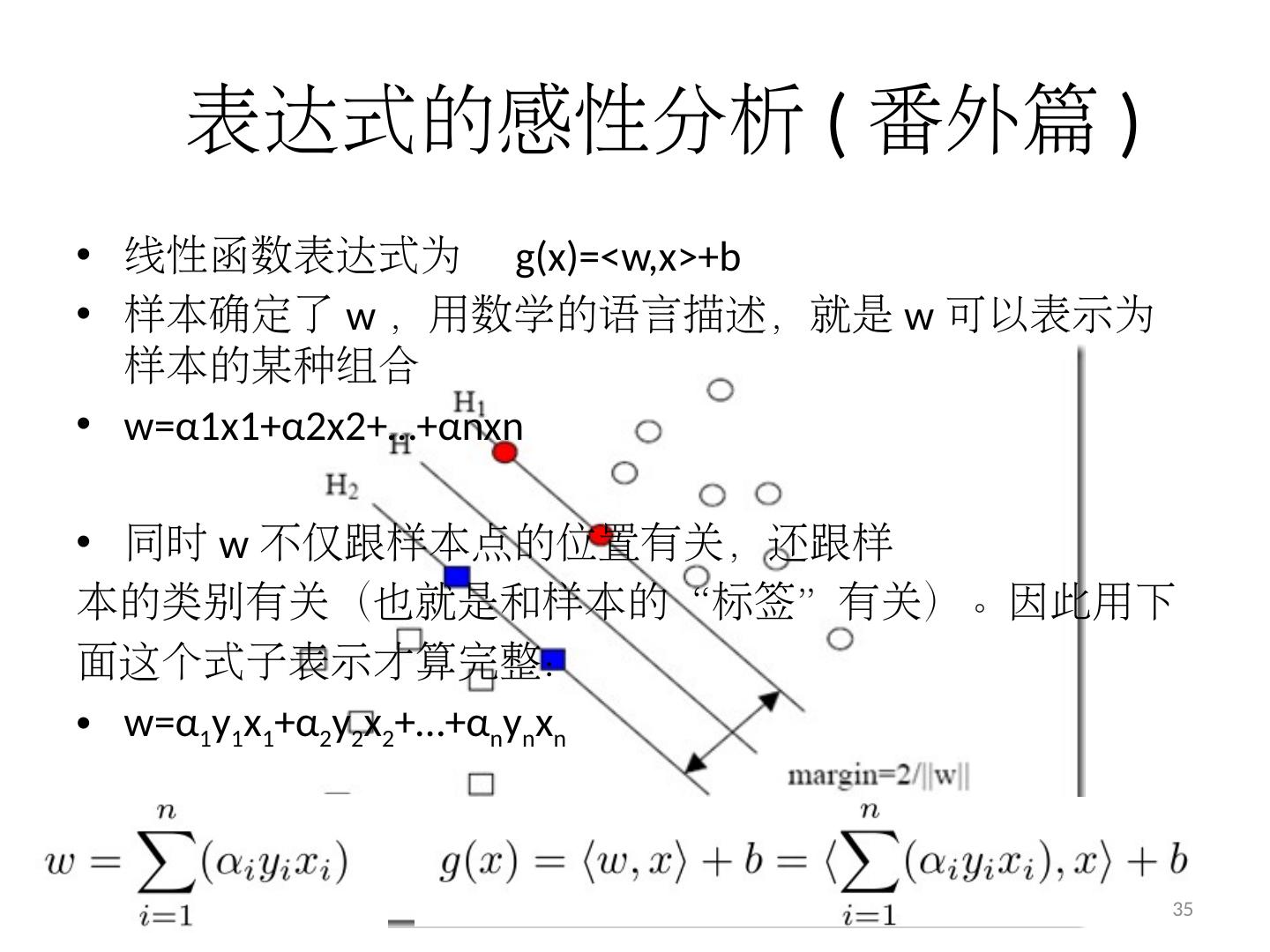
25 .几何间隔的现实含义 H 是分类面,而 H 1 和 H 2 是平行于 H ,且过离 H 最近的两类样本的直线, H 1 与 H , H 2 与 H 之间的距离就是几何 间隔 25
26 .几何间隔 的存在意义 几何间隔与样本的误分次数间存在 关系 其中的 δ 是样本集合到分类面的间隔, R=max ||xi|| i =1,...,n ,即 R 是所有样本 中向量 长度最长的值(也就是说代表样本的分布有多么广 ) 误分 次数一定程度上代表分类器的误差 。(证明略) 误 分次数的上界由几何间隔 决定(样本 已知的时候) 26
27 .Maximum Margin 为了使分类面更合适 为了减少误分次数 最大化几何间隔 27
28 .minimize ||w|| 是否让 W=0 ,目标函数就最小了呢? = 。 = 式子有还有一些限制条件,完整的写下来,应该是这样 的 求最小值的问题就是一个优化 问题,一 个带约束的二次规划 (quadratic programming, QP) 问题,是一个凸 问题 凸二次规划区别于一般意义上的规划问题, 它有 解而且是 全局最优的解 ,而且 可以找到 28
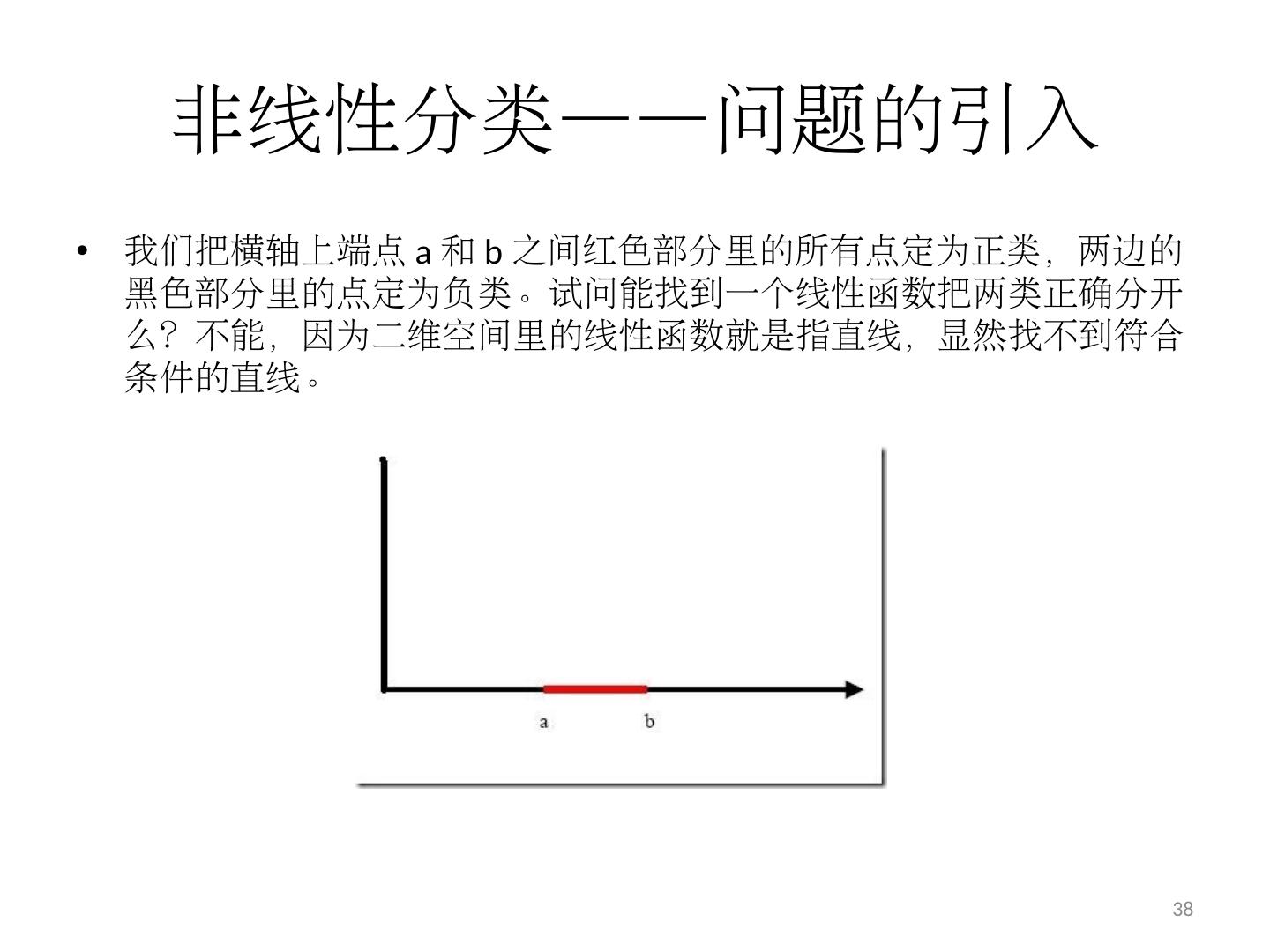
29 .如何解二次规划问题 等式约束,是求极值、拉格朗日转化等方法转化为无约束问题 不等式约束 的 问题怎么办? 方法 一 :用 现成的 QP (Quadratic Programming) 优化包进行 求解 ( 效率低 ) 方法 二:求解与原问题等价的对偶 问题 (dual problem) 得到 原始问题的 最优解 ( 更易求解、可以推广到核函数 ) 拉格朗日乘子法 拉格朗日对偶性 KKT 理论支撑 29