3. 高性能联邦学习算法优化实践

1 .FATE: ⾼性能联邦学习算法优化实践 ⻢国强 微众银⾏⾼级研究员 

2 .01 联邦学习分类 

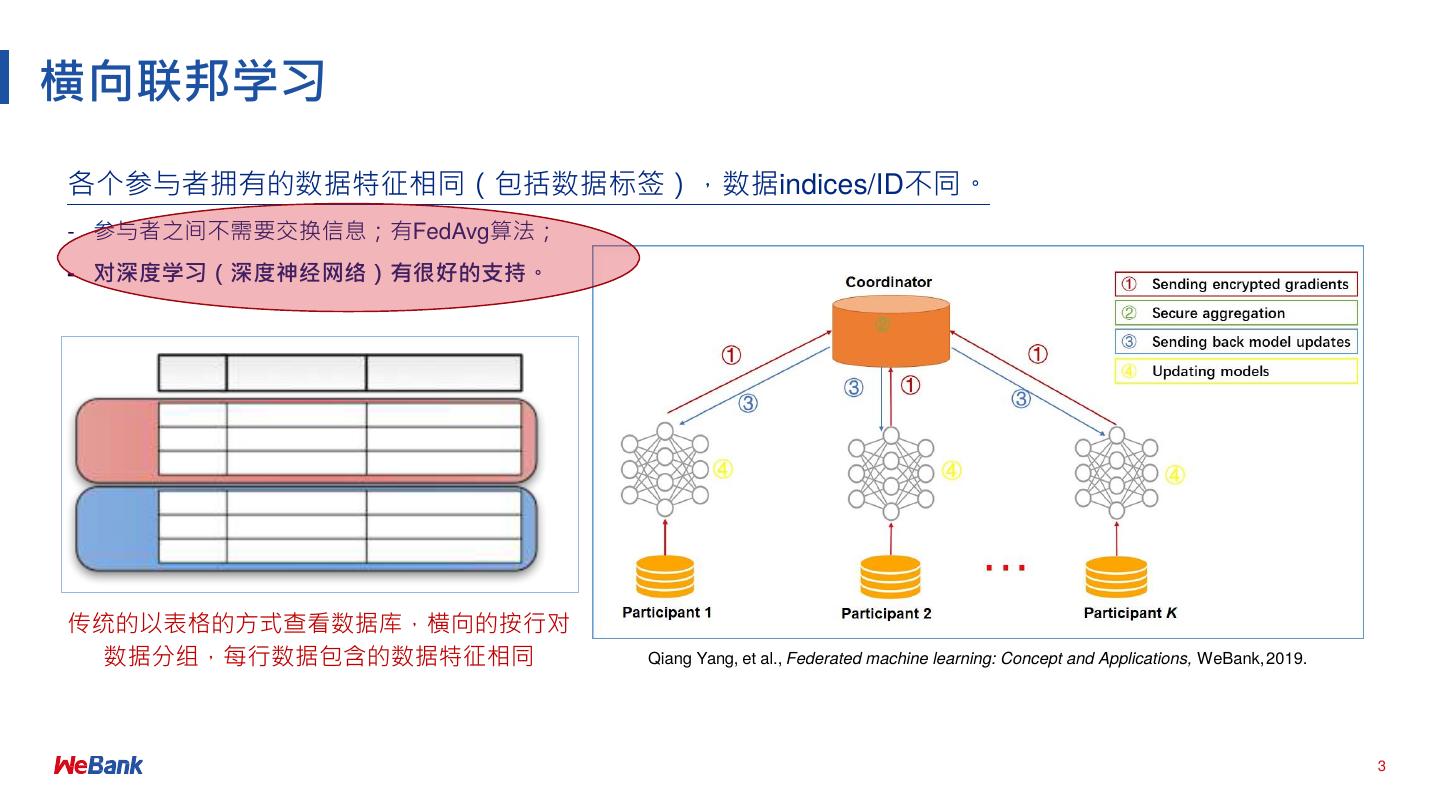
3 .横向联邦学习 各个参与者拥有的数据特征相同（包括数据标签），数据indices/ID不同。 - 参与者之间不需要交换信息；有FedAvg算法； - 对深度学习（深度神经⽹络）有很好的⽀持。 传统的以表格的⽅式查看数据库，横向的按⾏对 数据分组，每⾏数据包含的数据特征相同 Qiang Yang, et al., Federated machine learning: Concept and Applications, WeBank, 2019. 3 

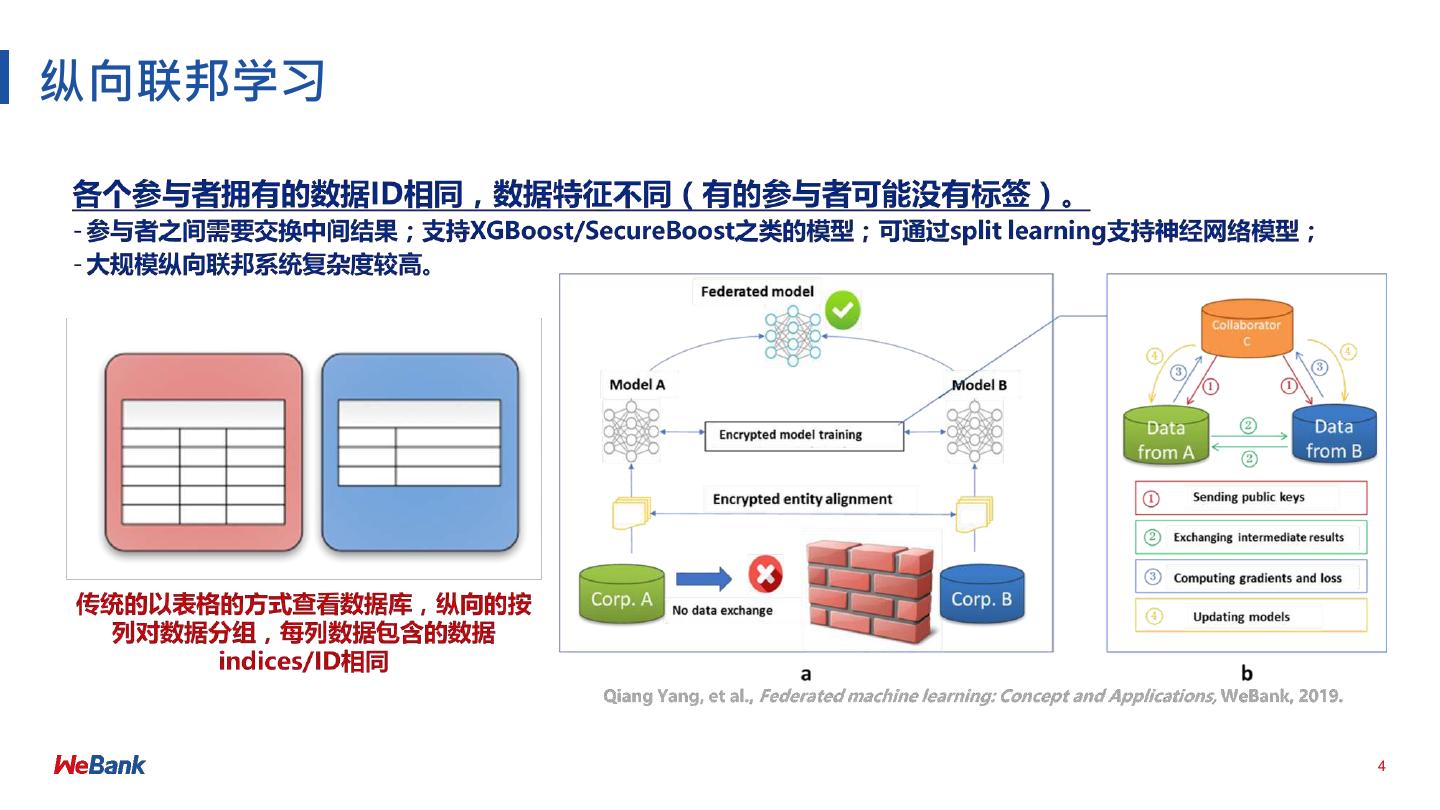
4 .纵向联邦学习 4 

5 .02 FATE-FederatedML 

6 .FATE 愿景 • ⼯业级别联邦学习系统 • 有效帮助多个机构在符合数据安全和政府法规前提下，进⾏数据使⽤和 联合建模 设计原则 • ⽀持多种主流算法：为机器学习、深度学习、迁移学习提供⾼性能联邦 学习机制 • ⽀持多种多⽅安全计算协议：同态加密、MPC-SPDZ、OT等 • 友好的跨域交互信息管理⽅案，解决了联邦学习信息安全审计难的问题 Github https://github.com/FederatedAI/ Website • https://FedAI.org 

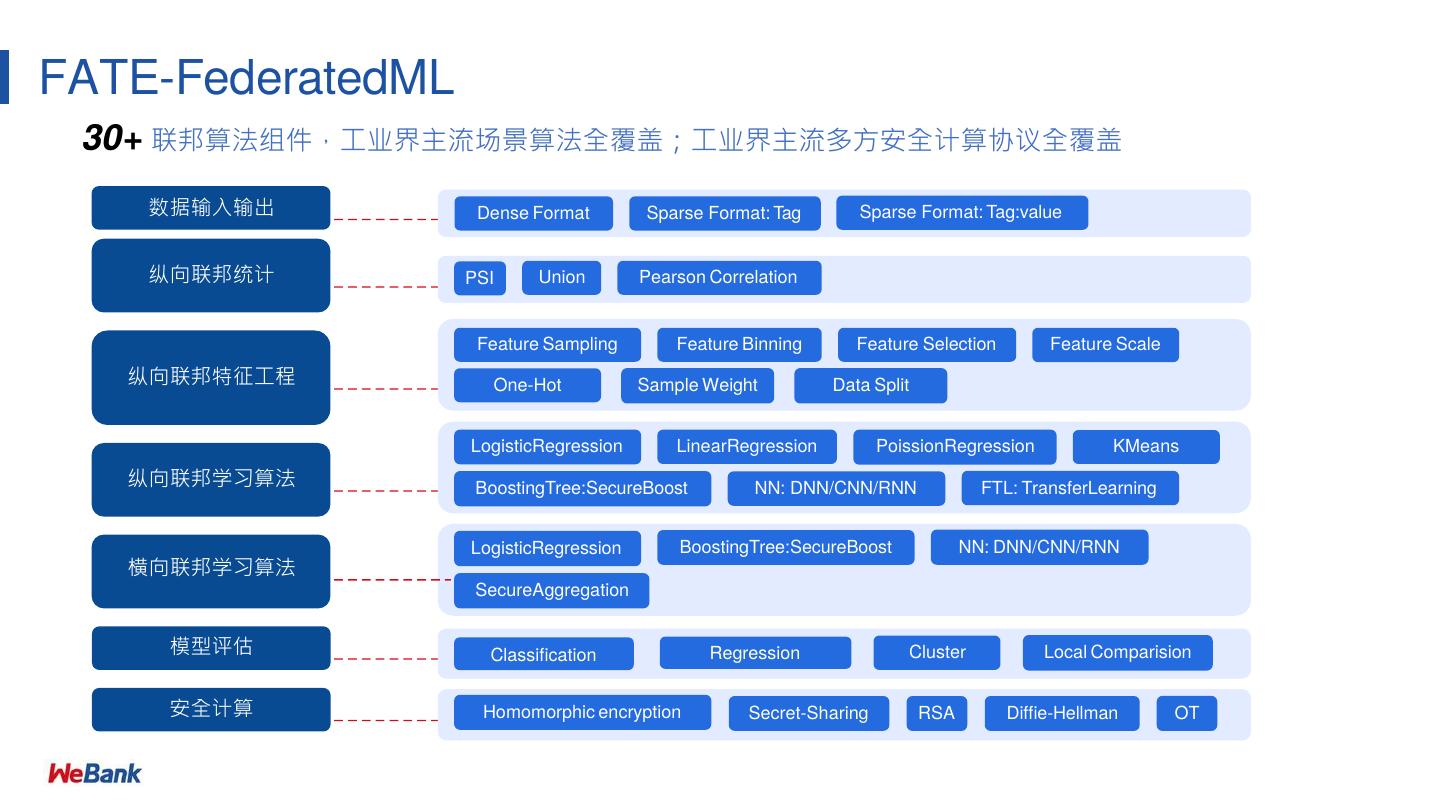
7 .FATE-FederatedML 30+ 联邦算法组件，⼯业界主流场景算法全覆盖；⼯业界主流多⽅安全计算协议全覆盖 数据输⼊输出 Dense Format Sparse Format: Tag Sparse Format: Tag:value 纵向联邦统计 PSI Union Pearson Correlation Feature Sampling Feature Binning Feature Selection Feature Scale 纵向联邦特征⼯程 One-Hot Sample Weight Data Split LogisticRegression LinearRegression PoissionRegression KMeans 纵向联邦学习算法 BoostingTree:SecureBoost NN: DNN/CNN/RNN FTL: TransferLearning LogisticRegression BoostingTree:SecureBoost NN: DNN/CNN/RNN 横向联邦学习算法 SecureAggregation 模型评估 Classification Regression Cluster Local Comparision 安全计算 Homomorphic encryption Secret-Sharing RSA Diffie-Hellman OT 

8 .03 联邦学习算法性能优化实践 

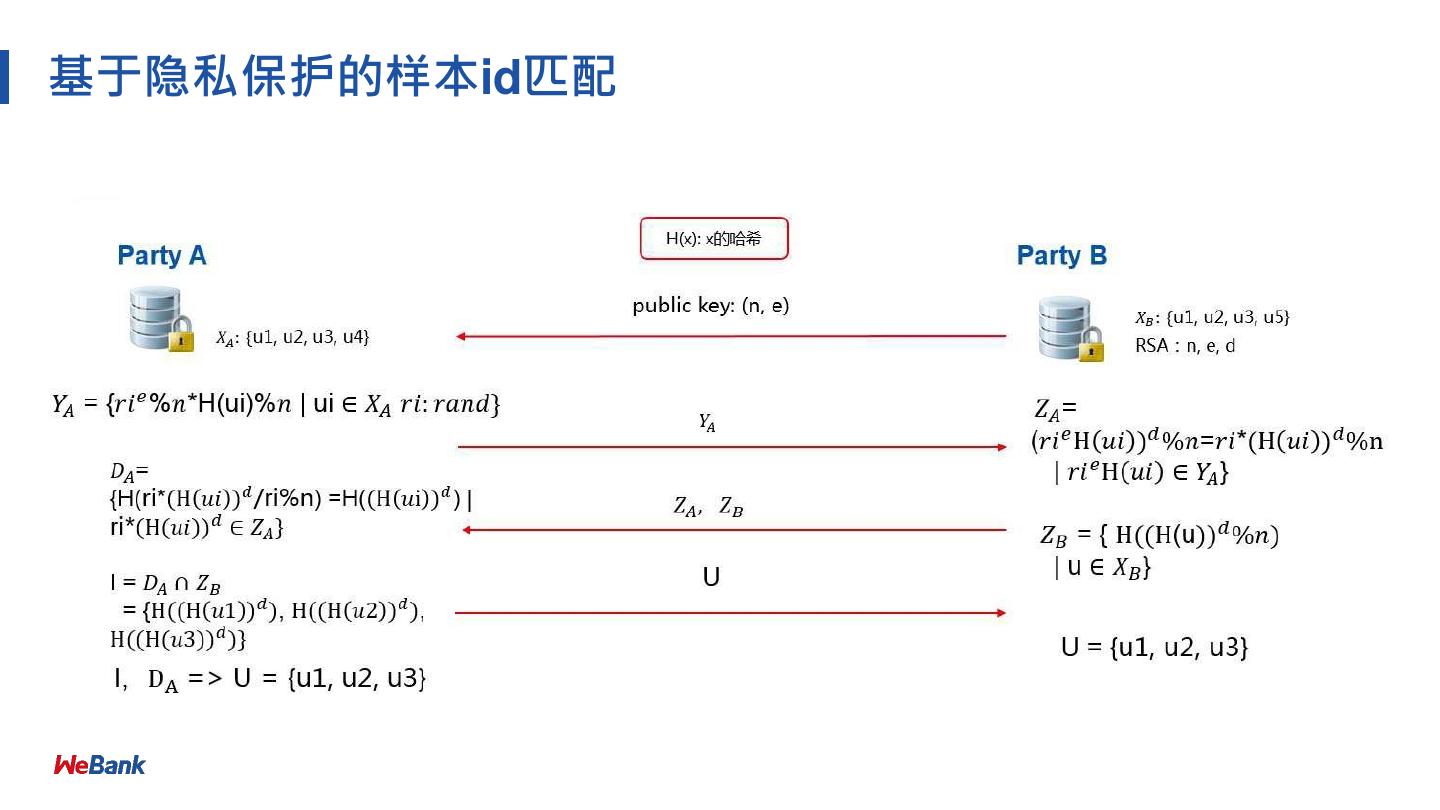
9 .基于隐私保护的样本id匹配 如何寻找交集: 𝑋 ∩ 𝑌=[u1, u2, u3] ？ 满⾜条件： ✓ Party A 不知道Party B 有 u5 ✓ Party B 不知道 Party A 有u4 解决⽅案： RSA + 哈希机制的安全求交⽅案 [u1, u2, u3, u4] [u1, u2, u3, u5] ID set X ID set Y Party A Party B https://github.com/FederatedAI/FATE/tree/master/python/federatedml/statistic/intersect 9 

10 .基于隐私保护的样本id匹配 

11 .基于隐私保护的样本id匹配 • 性能优化1-随机数复⽤ • YA: 计算主要耗时为系统随机数⽣成和幂模运算r^e，预先⽣成特定⽐例的r^e，样本随机复⽤ 11 

12 .基于隐私保护的样本id匹配 • 性能优化2-算⼒均衡 • 耗时分析： • A⽅计算耗时： • YA-随机数产⽣和幂模运算，其中幂指数RSA公钥e⼀般为65537 • DA: 除法运算 • B⽅计算耗时： • ZA-幂模运算，幂指数RSA私钥d位⻓⼀般>=bit(n) - bit(e) • ZB-幂模运算，幂指数为RSA私钥d • 优化：可通过数据分组，如对H(u) % 2进⾏分组，两⽅使⽤相应数据进⾏正反RSA交集运算，使得双⽅计 算对等 

13 .基于隐私保护的样本id匹配 • 性能优化3-CRT优化 • RSA: n = p * q, p, q 为随机⼤素数 • 中国剩余定理: • ZA = YA^d % n => CRT(YA^(d%(p - 1)) % p, YA^(d%(q - 1)) % q)，通过降低幂运算次数和模数再合并， 加速ZA运算过程 • ZB同理 

14 .基于隐私保护的样本id匹配 • 性能优化4-粗细结合(主要针对不平衡数据集) • Step1: 结果粗选。 • 交集数⼩的⼀⽅，产⽣BloomFilter并保证⾜够的误差率，发送给另⼀⽅，快速过滤出可能的候选集 • Step2: 执⾏正常的RSA交集流程 

15 .基于隐私保护的样本id匹配 • 性能优化5-离线预处理 • 离线阶段(⼀次) • 注意到：对于ZB，只依赖于B⽅的id和私钥d，预处理ZB • 将ZB发给A⽅ • 在线阶段(任意次) • 修改原RSA交集流程，ZB的计算和发送步骤忽略 

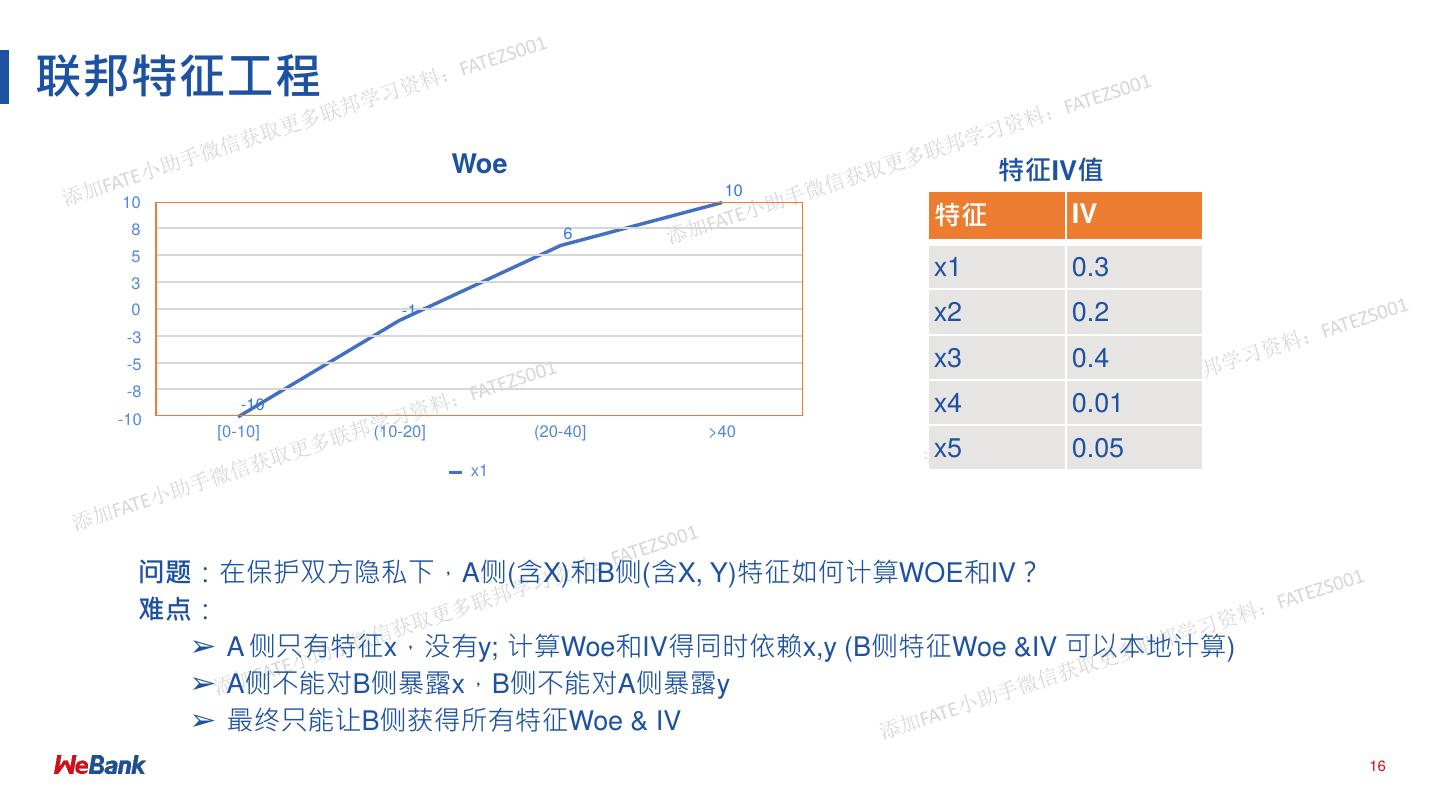
16 .联邦特征⼯程 Woe 特征IV值 10 特征 10 8 IV 6 5 x1 0.3 3 0 -1 x2 0.2 -3 -5 x3 0.4 -8 -10 -10 x4 0.01 [0-10] (10-20] (20-40] >40 x5 0.05 x1 问题：在保护双⽅隐私下，A侧(含X)和B侧(含X, Y)特征如何计算WOE和IV？ 难点： ➢ A 侧只有特征x，没有y; 计算Woe和IV得同时依赖x,y (B侧特征Woe &IV 可以本地计算) ➢ A侧不能对B侧暴露x，B侧不能对A侧暴露y ➢ 最终只能让B侧获得所有特征Woe & IV 16 

17 . Encry(x): x的加法同态加密， A: Xi (特征分箱) Encode(x): 本地编码 B: (X,Y) 1. {idi , Encry(yi), Encry(1-yi)} 2. { Encode(id_set_i), sum(Encry(yi)), 3. sum(Encry(1-yi)) npos_i = } Decry(sum(Encry(yi))); nneg_i = Decry(sum(Encry(1-yi))) B ⽅本地计算 1. distpos_i = npos_i/pos_total; distneg_i =nneg_i/neg_total 2. Woe_i = 100 * log(distpos_i / distneg_i) 𝑘 3. IV = ∑ (𝑑𝑖𝑠𝑝𝑜𝑠_𝑖 − 𝑑𝑖𝑠𝑛𝑒𝑔_𝑖)∗log(𝑑𝑖𝑠𝑝𝑜𝑠_𝑖/𝑑𝑖𝑠𝑛𝑒𝑔_𝑖) 𝑖=1 

18 .联邦特征⼯程 • 性能优化1: • y = 0 or 1 => sum([[1 - y]]) + sum([[y]]) = N, N 为样本数 • 对于Step2的每个id_set_i，只计算sum([[yi]])，sum([[1 - yi]]) = |id_set_i| - sum([[yi]]) • 同态加密加法运算次数 2 * N * Shape -> (N * Shape) 18 

19 .联邦特征⼯程 • 性能优化2: • 对于互联⽹特别⼴告数据⽽⾔，稀疏数据为主 • 计算id_set_1, id_set_2… id_set_max的sum([yi])、sum([[1 - yi]])，max为分箱总数 • id_set_0: sum_0([[y]]) = N - sum_1([[yi]]) - sum_2([[yi)]] - … - sum_max([[yi]])，sum_0([[1 - yi]])类似 得到 • 同态加密加法运算次数: N * Shape => ⾮0特征总量 19 

20 .联邦特征⼯程 • 性能优化3: • sum([[yi]]) <= max(sum([1])) <= N, N为样本数，同理 sum([[1 - yi]]) <= N • paillier半同态加密能表达的范围为[-2^key_length/3, 2^key_length/3]，key_length=1024或者2048或3072 • 若⼲个对象压缩为⼀组，即 ((((((sum_0([[yi]]) * base) + sum_1([[yi]])) * base) + …))) + sum_k[[yi]] • sum_0 = [[1]], sum_1 = [[2]], sum_2 = [[3]], sum_3 = [[4]], base = 10，4个对象压缩成1个 • ((([[1]] * 10 + [[2]]) * 10 + [[3]]) * 10) + [[4]] = [[1234]] • A给B⽅传输压缩对象，B⽅拿到后解密后再解压缩 • decrypt([[1234]] ) = 1234 • sum_3 = 1234 % 10, sum_2 = (1234/10) % 10 = 3, sum_1 = (1234 / 100) % 10 = 2, sum_0 = 1 • 密⽂压缩后，A⽅给B⽅的传输加密数据量由 2 * Shape * Bin_num降低为 2 * Shape * Bin_num / 每组压缩 对象个数，同理，B⽅解密运算量同步降低 20 

21 .联邦特征⼯程 • 性能优化4(多分类): • 多分类Binning IV值：求出在每种标签下的iv值，⽤于后续特征选择等 • 1. 将标签OneHot：yi => [0, 0, 0. …, 1, 0, 0]，只有pos = yi的位置为1，其他为0 • 2. 对数据特征进⾏分箱 • 3. 枚举每个标签index，重复求IV值过程: • 数据格式为(label_index, id_set_i, sum(([[yi]]), sum(([[1 - yi]])) • 观察: 对于label_index，id_set_i⾥⾯的样本id完全⼀致 => 如⼲个标签压缩为⼀组⼀起求和 • 标签压缩： • sum([[yi_label_0 * Base + yi_label_1) * Base + yi_label_2…]]) = (sum([[yi_label_0]]) * Base + sum([[yi_label_1]])) * Base + …. 21 

22 .联邦特征⼯程 • 性能优化4(多分类): • 标签压缩： • 假设为三分类，6个样本为[0, 0, 1], [0, 1, 0], [1, 0, 0], [0, 0, 1], [0, 1, 0], [0, 1, 0] • 不妨选择base = 10，压缩结果为1, 10, 100, 1, 10, 10 • sum(1 + 10 + 100 + 1 + 10 + 10) = sum(132) • 解码： • label_2: 132 % 10 = 2, • label_1: 132 / 10 % 2 = 3, • label_0: 132 / 10 = 1 • 加密计算量：2 * |classes| * N * Shape => 2 * |classes| * N * Shape / 组内压缩标签数 • 解密计算量：2.* |classes| * Shape * Bin_num => 2 * |classes| * Shape * Bin_num / 组内压缩标签数 22 

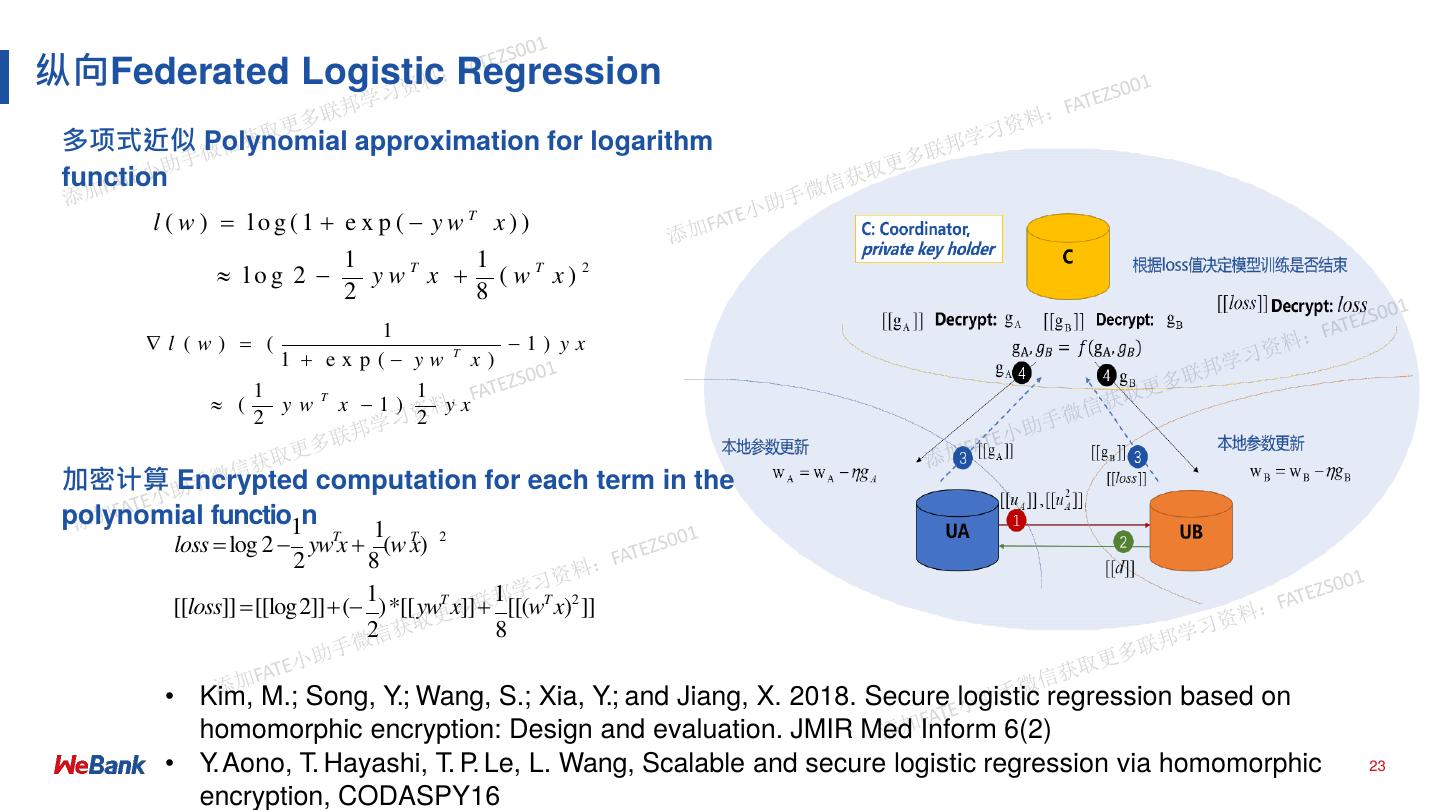
23 .纵向Federated Logistic Regression 多项式近似 Polynomial approximation for logarithm function l ( w )  log(1  e x p (  ywT x)) 1 1  log 2  ywT x  ( wT x) 2 2 8 1 l (w)  ( 1) yx 1  exp( yw T x) 1 1  ( ywT x 1) yx 2 2 加密计算 Encrypted computation for each term in the polynomial functio1n 1 loss  log 2  ywTx  (w x) T 2 2 8 1 1 [[loss]] [[log2]]( )*[[ywT x]] [[(wT x)2 ]] 2 8 • Kim, M.; Song, Y.; Wang, S.; Xia, Y.; and Jiang, X. 2018. Secure logistic regression based on homomorphic encryption: Design and evaluation. JMIR Med Inform 6(2) • Y. Aono, T. Hayashi, T. P. Le, L. Wang, Scalable and secure logistic regression via homomorphic 23 encryption, CODASPY16 

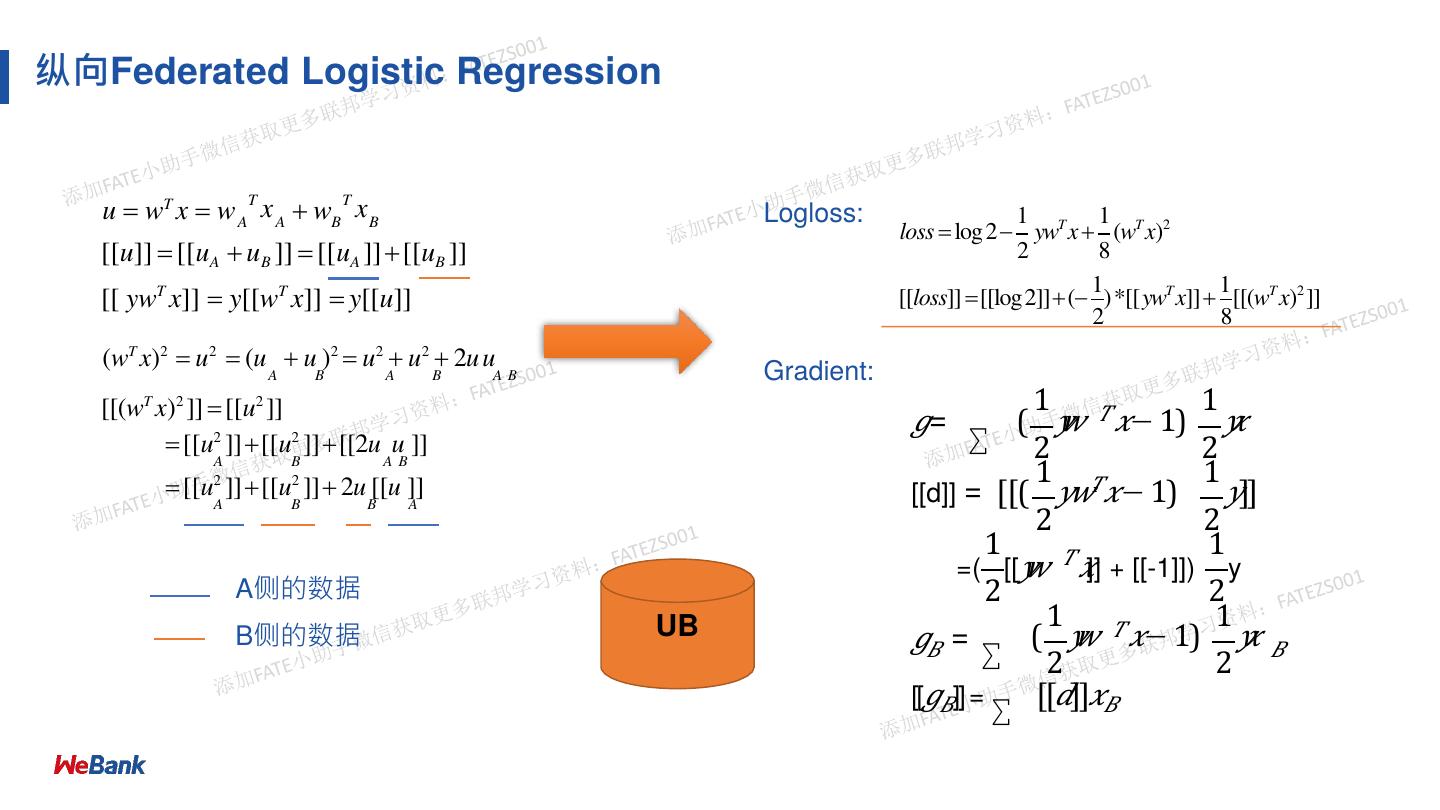
24 .纵向Federated Logistic Regression u  wT x  w A x A  wB x B T T Logloss: 1 1 loss  log 2 ywT x  (wT x)2 [[u]]  [[uA  uB ]]  [[uA ]]  [[uB ]] 2 8 1 1 [[ ywT x]]  y[[wT x]]  y[[u]] [[loss]] [[log2]]( )*[[ywT x]] [[(wT x)2 ]] 2 8 (wT x)2  u2  (u  u )2  u2  u2  2u u A B A B AB Gradient: [[(wT x)2 ]]  [[u2 ]] 1 1 𝑔= ∑ ( 𝑦𝑤 𝑇 𝑥− 1) 𝑦𝑥  [[u2 ]][[u2 ]][[2u u ]] 2 2 1 1 A B A B  [[u ]][[u ]] 2u [[u ]] [[d]] = [[( 𝑦𝑤𝑇𝑥− 1) 𝑦]] 2 2 A B B A 2 2 1 𝑇 1 =( [[𝑦𝑤 𝑥]] + [[-1]]) y A侧的数据 2 2 1 𝑇 1 B侧的数据 UB 𝑔𝐵 = ∑ ( 𝑦 𝑤 𝑥− 1) 𝑦𝑥 𝐵 2 2 [[𝑔𝐵]] = ∑ [[𝑑]]𝑥𝐵 

25 .纵向Federated Logistic Regression • 性能优化1: • [[d]]计算并⾏ • PPT中第⼀步[[U_A]] host计算完成后发给guest，第⼆步guest计算[[d]]，然后发给[[Host]] • 事实上，因为y=+/-1，所以y^2=1，拆解公式，[[d]]的计算可并⾏ • Guest\Host同步计算[[d]]， 

26 .纵向Federated Logistic Regression • 性能优化2: • [[d]] * X计算优化，使⽤低精度，如X = int(round(X * 2**23)) 

27 .纵向Federated Logistic Regression • 性能优化3: • Python paillier优化 • fate_paillier的代码或者pypi的phe代码: 两加密数相加，使⽤的原⽣python语法 • 将e_x和e_y转成gmpy2.mpz对象加速 

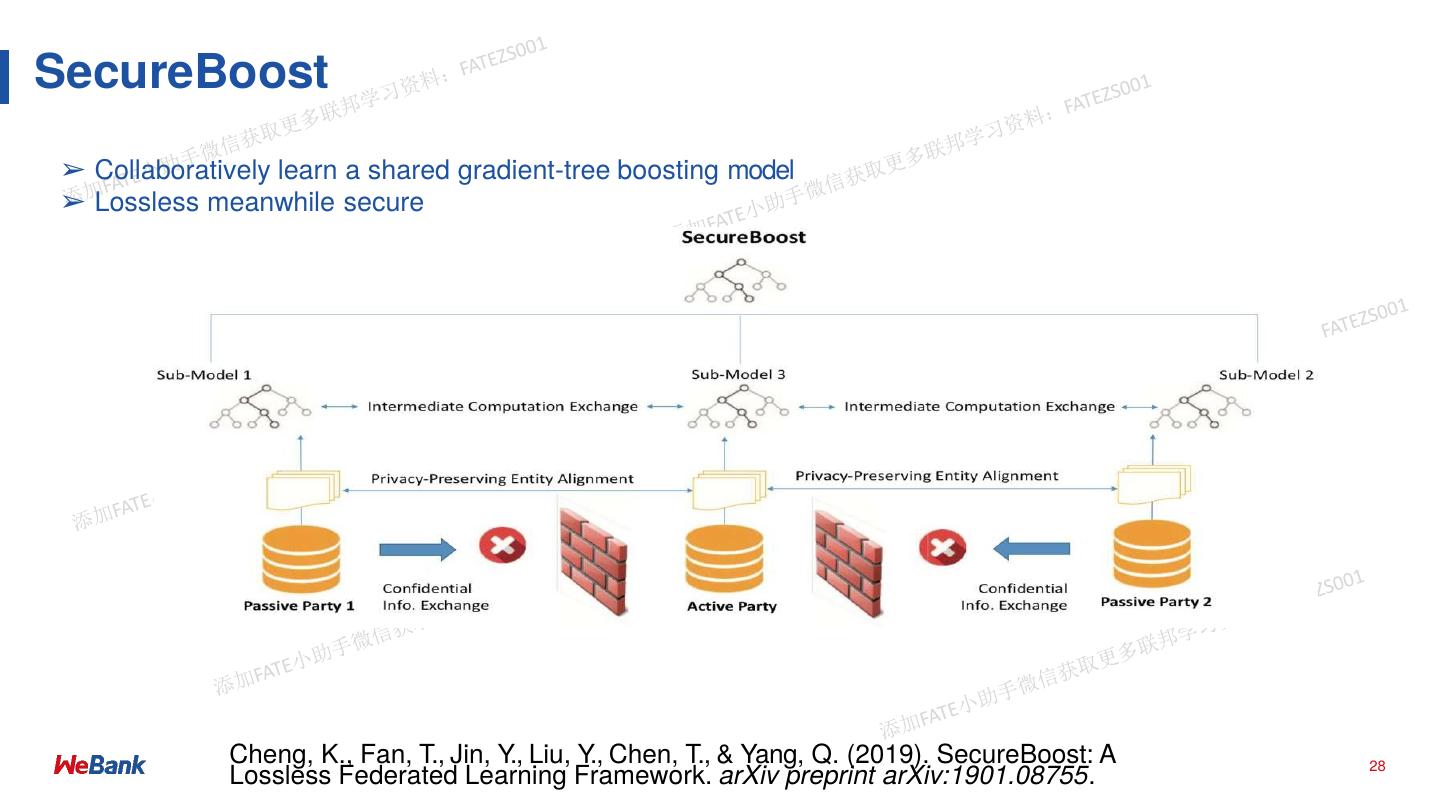
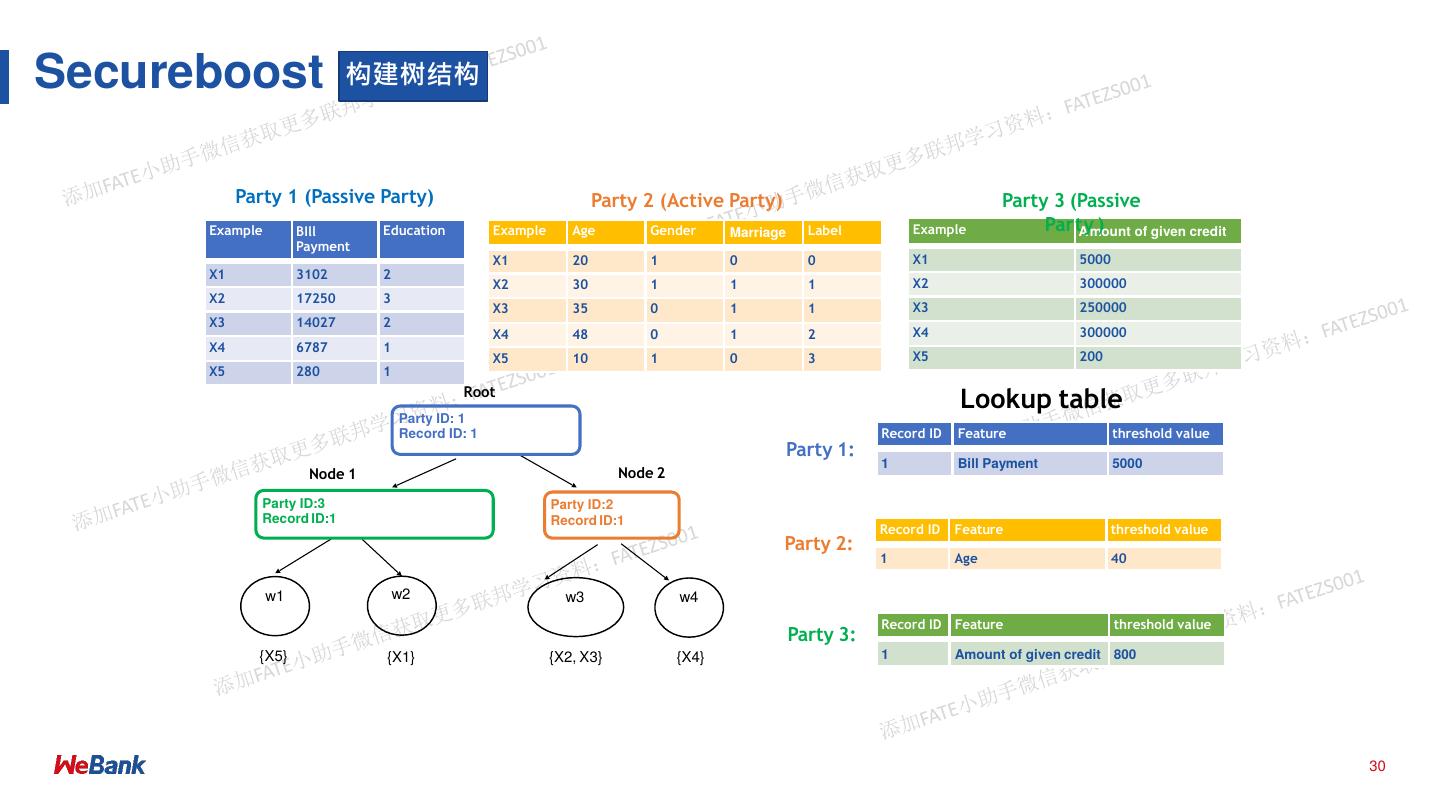
28 .SecureBoost ➢ Collaboratively learn a shared gradient-tree boosting model ➢ Lossless meanwhile secure Cheng, K., Fan, T., Jin, Y., Liu, Y., Chen, T., & Yang, Q. (2019). SecureBoost: A 28 Lossless Federated Learning Framework. arXiv preprint arXiv:1901.08755. 

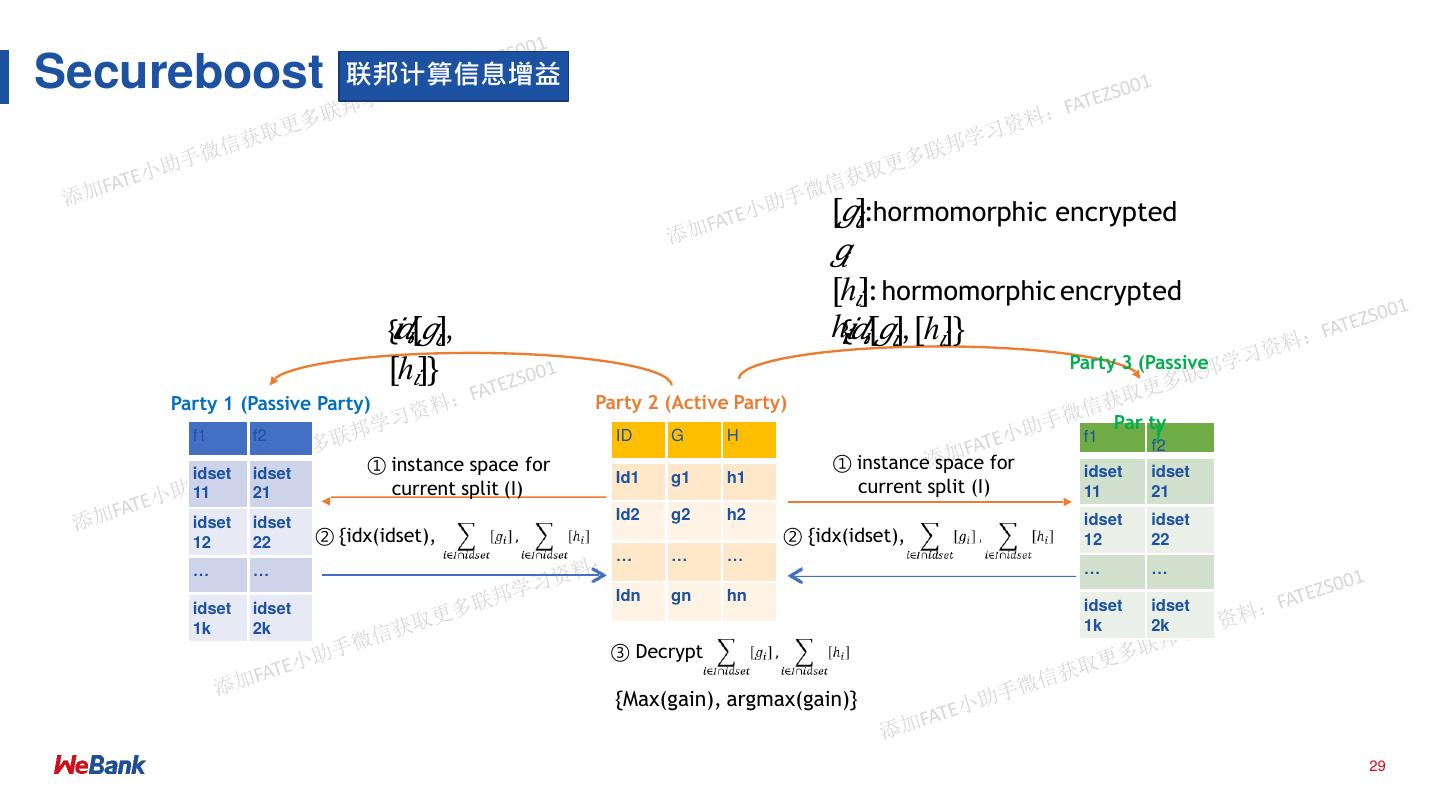
29 .Secureboost 联邦计算信息增益 [𝑔𝑖]:hormomorphic encrypted 𝑔𝑖 [ℎ𝑖]: hormomorphic encrypted {𝑖𝑑𝑖,[𝑔𝑖], ℎ𝑖{𝑖𝑑𝑖,[𝑔𝑖], [ℎ𝑖]} [ℎ𝑖]} Party 3 (Passive Party 1 (Passive Party) Party 2 (Active Party) Par ty ) f1 f2 ID G H f1 f2 ① instance space for ① instance space for idset idset idset idset Id1 g1 h1 11 21 current split (I) current split (I) 11 21 idset idset Id2 g2 h2 idset idset 12 22 ② {idx(idset), ② {idx(idset), 12 22 … … … … … … … Idn gn hn idset idset idset idset 1k 2k 1k 2k ③ Decrypt {Max(gain), argmax(gain)} 29